Web3 Uniswap DEX Development Book
Useful Links
- This book is hosted on GitHub: https://github.com/yuhuajing/uniswap-book
- Page in https://yuhuajing.github.io/uniswap-book/
Table of Contents
- 背景
- uniswapV1
- uniswapV2
- uniswapV3
Running locally
To run the book locally:
- Install Rust.
- Install mdBook:
$ cargo install mdbook $ cargo install mdbook-katex - Clone the repo:
$ git clone https://github.com/yuhuajing/uniswap-book.git $ cd uniswap-book - Run:
$ mdbook serve --open - Visit http://localhost:3000/ (or whatever URL the previous command outputs!)
Fixed point 定点数计算
Solidity 中的定点运算(以 Solady、Solmate 和 ABDK 为例)
定点数是仅存储分数分子的整数,而分母是隐含的。
在大多数编程语言中,这种类型的运算是不必要的,因为它们有浮点数。但在 Solidity 中,这种运算是必要的,因为 Solidity 只有整数,而我们经常需要对小数进行运算。
大多数 DeFi 智能合约中都有定点数,因此了解它们是必须的。
例如,如果“隐含分母”是 100,则保留“10”的定点数将被解释为 $\frac{10}{100} = 0.1 $。
Solidity 中最常见的定点数是 $10^{18}$ ,以太坊和大多数 ERC-20 代币的“小数”数量。当我们读取以太坊地址的余额时,我们会隐式地将该数字除以 $10^{18}$ 确定其 Ether 数量。
例如,一个地址的余额为 $10^{19}$ 被解释为有 10 个 Ether — 因为除以 $10^{18}$ 是隐含的。
分母为 $10^{18}$ 非常常见,Solidity 社区的工程师将其称为“Wad”(该名称最初由 MakerDAO 引入)。有时,18 位定点数被解释为将最右边的 18 位数字分配给小数,例如,数字“10”如下所示:
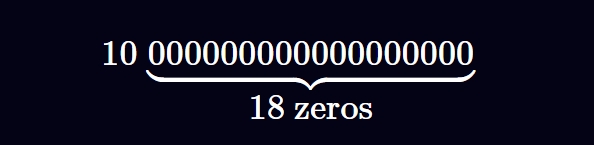
将整数转换为定点数
要将整数转换为定点数,请将整数乘以隐含的分母。例如,2 Ether 是 $2 * 10^{18}$
定点数乘法
要将两个定点数相乘,我们遵循分数乘法的规则:
- 将分子相乘
- 将分母相乘
- 简化结果。
例如:$\frac{x}{d} * \frac{y}{d} = z $,其中
x,y表示 定点数,d表示分母,z表示将定点数相乘的结果转成整数
如果我们想把定点数相乘的结果也转化成定点数的话,整式结果需要乘以分母,即 z * d
继续化简为: $z * d = \frac{x}{d} * \frac{y}{d} * d = \frac{x * y}{d} $
乘以定点的代码示例
Solady 库有一个 mulWad 数学运算,可以将两个定点数与隐含的 Wad 分母相乘($10^{18}$)。下面,我们展示代码,然后解释它与我们之前的讨论有何关联:
/// @dev The scalar of ETH and most ERC20s.
uint256 internal constant WAD = 1e18;
/*´:°•.°+.*•´.*:˚.°*.˚•´.°:°•.°•.*•´.*:˚.°*.˚•´.°:°•.°+.*•´.*:*/
/* SIMPLIFIED FIXED POINT OPERATIONS */
/*.•°:°.´+˚.*°.˚:*.´•*.+°.•°:´*.´•*.•°.•°:°.´:•˚°.*°.˚:*.´+°.•*/
/// @dev Equivalent to `(x * y) / WAD` rounded down.
function mulWad(uint256 x, uint256 y) internal pure returns (uint256 z) {
/// @solidity memory-safe-assembly
assembly {
// Equivalent to `require(y == 0 || x <= type(uint256).max / y)`.
if gt(x, div(not(0), y)) {
// x * y > type(uint256).max
if y { // y != 0
mstore(0x00, 0xbac65e5b) // `MulWadFailed()`.
revert(0x1c, 0x04)
}
}
z := div(mul(x, y), WAD)
}
}
假设一个用户有 1 DAI(有 18 位小数),我们希望计算他们的余额,假设他们的存款获得了 15% 的利息。这是一个需要定点运算的明显例子,因为我们不能在 Solidity 中直接将一个数字乘以 1.15。
import "https://github.com/Vectorized/solady/blob/main/src/utils/FixedPointMathLib.sol";
contract C {
using FixedPointMathLib for uint256;
uint256 tokenBalance = 1e18;
function compute15PInterest() public view returns (uint256) {
return tokenBalance.mulWad(1.15e18);
} // 1150000000000000000
}
定点数除法
要将两个定点数相除,我们遵循分数除法的规则:
-
反转除数,将除法变成乘法
-
将分子相乘
-
将分母相乘
-
简化结果。
-
例如:$\frac{x}{d} / \frac{y}{d} = \frac{x}{d} * \frac{d}{y} = z $,其中
x,y表示 定点数,d表示分母,z表示将定点数相乘的结果转成整数
如果我们想把定点数相除的结果也转化成定点数的话,整式结果需要乘以分母,即 z * d
继续化简为: $z * d = \frac{x}{d} * \frac{d}{y} * d = \frac{x * d}{y} $
/// @dev Equivalent to `(x * WAD) / y` rounded down.
function divWad(uint256 x, uint256 y) internal pure returns (uint256 z) {
/// @solidity memory-safe-assembly
assembly {
// Equivalent to `require(y != 0 && x <= type(uint256).max / WAD)`.
if iszero(mul(y, lt(x, add(1, div(not(0), WAD))))) {
mstore(0x00, 0x7c5f487d) // `DivWadFailed()`.
revert(0x1c, 0x04)
}
z := div(mul(x, WAD), y)
}
}
加定点数
要将两个定点数相加,我们遵循加减法的规则:
-
分母不变
-
将分子相加
-
简化结果。
-
例如:$\frac{x}{d} + \frac{y}{d} = \frac{x + y}{d} = z $, 其中
x,y表示 定点数,d表示分母,z表示将定点数相乘的结果转成整数
如果我们想把定点数相除的结果也转化成定点数的话,整式结果需要乘以分母,即 z * d
继续化简为: $z * d = \frac{x + y}{d} * d = x + y $
减定点数
要将两个定点数相减,我们遵循加减法的规则:
-
分母不变
-
将分子相减
-
简化结果。
-
例如: $\frac{x}{d} - \frac{y}{d} = \frac{x - y}{d} = z $, 其中
x,y表示 定点数,d表示分母,z表示将定点数相乘的结果转成整数
如果我们想把定点数相除的结果也转化成定点数的话,整式结果需要乘以分母,即 z * d
继续化简为: $z * d = \frac{x - y}{d} * d = x - y $
二进制与十进制定点数
二进制定点数是分母可以表示为 $2^{n}$
二进制定点数通常用 Q 符号表示。例如,UQ112x112 使用 $2^{112}$ 作为分母。U 表示“无符号”。用于保存 UQ112x112 的数据类型为 uint224: $2^{112} * 2^{112} = 2^{224}$。
另一个例子是,UQ64x64(或 UQ64.64)将 uint128 “小数部分”保存在最低有效 64 位中,将“整数”保存在最高有效位中。
二进制定点数的优点是我们可以使用节省 gas 的左/右位移位而不是乘以分母(将整数转换为定点数时,或在除法时进行右位移位)。
举个基本的例子,考虑以下情况:
2的二进制表示形式为1016的二进制表示形式为1000016 = 2 *$2 ^ {3}$, 二进制表示为:10000 = 10 << 3
二进制运算如下:
x * $2 ^ {112} == x << 112
x / $2 ^ {112} == x >> 112 , x 可以是任意数字,只要它适合无符号整数。
ABDK 库
ABDK 库 fromUInt 函数代码将 int256 的值转成 Q64.64 = int128 类型
function fromInt (int256 x) internal pure returns (int128) {
unchecked {
require (x >= -0x8000000000000000 && x <= 0x7FFFFFFFFFFFFFFF);
return int128 (x << 64);
}
}
/**
* Convert signed 64.64 fixed point number into signed 64-bit integer number
* rounding down.
*
* @param x signed 64.64-bit fixed point number
* @return signed 64-bit integer number
*/
function toInt (int128 x) internal pure returns (int64) {
unchecked {
return int64 (x >> 64);
}
}
/**
* Convert unsigned 256-bit integer number into signed 64.64-bit fixed point
* number. Revert on overflow.
*
* @param x unsigned 256-bit integer number
* @return signed 64.64-bit fixed point number
*/
function fromUInt (uint256 x) internal pure returns (int128) {
unchecked {
require (x <= 0x7FFFFFFFFFFFFFFF);
return int128 (int256 (x << 64));
}
}
/**
* Convert signed 64.64 fixed point number into unsigned 64-bit integer
* number rounding down. Revert on underflow.
*
* @param x signed 64.64-bit fixed point number
* @return unsigned 64-bit integer number
*/
function toUInt (int128 x) internal pure returns (uint64) {
unchecked {
require (x >= 0);
return uint64 (uint128 (x >> 64));
}
}
ABDK mul 函数代码
二进制中使用位运算作为 wad,乘法示例如下:
function mul (int128 x, int128 y) internal pure returns (int128) {
unchecked {
int256 result = int256(x) * y >> 64;
require (result >= MIN_64x64 && result <= MAX_64x64);
return int128 (result);
}
}
Uniswap V2 定点库
Uniswap V2 的定点库非常简单,因为 Uniswap V2 对定点数执行的唯一操作是将定点数加法和除法与整数相加或相除。
pragma solidity =0.5.16;
// a library for handling binary fixed point numbers (https://en.wikipedia.org/wiki/Q_(number_format))
// range: [0, 2**112 - 1]
// resolution: 1 / 2**112
library UQ112x112 {
uint224 constant Q112 = 2**112;
// encode a uint112 as a UQ112x112
function encode(uint112 y) internal pure returns (uint224 z) {
z = uint224(y) * Q112; // never overflows
}
// divide a UQ112x112 by a uint112, returning a UQ112x112
// x * d / y
function uqdiv(uint224 x, uint112 y) internal pure returns (uint224 z) {
z = x / uint224(y);
}
}
encode() 函数将输入 uint112乘以定点数 Q112, 输出定点数 uint224
uqdiv() 函数只是将定点数除以整数,不需要额外的步骤。
Uniswap 使用此库来累积下方的 TWAP 预言机的价格。每次更新时,TWAP 都会将最新价格添加到累加器中(用于计算平均价格,但需要额外的步骤,这超出了本文的讨论范围)。由于价格以分数表示,因此定点数是理想的表示方式。
变量 _reserve0 和 _reserve1 保存池中最新的代币余额,并且是 uint112
price0CumulativeLast 和 price1CumulativeLast 是 UQ112x112
uniswap 中的 _update() 函数使用 UQ112X112 编码函数
function _update(uint balance0, uint balance1, uint112 _reserve0, uint112 _reserve1) private {
require(balance0 <= uint112(-1) && balance1 <= uint112(-1), 'UniswapV2: OVERFLOW');
uint32 blockTimestamp = uint32(block.timestamp % 2**32);
uint32 timeElapsed = blockTimestamp - blockTimestampLast; // overflow is desired
if (timeElapsed > 0 && _reserve0 != 0 && _reserve1 != 0) {
// * never overflows, and + overflow is desired
price0CumulativeLast += uint(UQ112x112.encode(_reserve1).uqdiv(_reserve0)) * timeElapsed;
price1CumulativeLast += uint(UQ112x112.encode(_reserve0).uqdiv(_reserve1)) * timeElapsed;
}
reserve0 = uint112(balance0);
reserve1 = uint112(balance1);
blockTimestampLast = blockTimestamp;
emit Sync(reserve0, reserve1);
}
向上舍入与向下舍入
定点库通常具有在除法时向上舍入的选项。例如,Solady 具有:
mulWadUp— 将两个定点数相乘,但除以d时向上舍入
/// @dev Equivalent to `(x * y) / WAD` rounded up.
function mulWadUp(uint256 x, uint256 y) internal pure returns (uint256 z) {
/// @solidity memory-safe-assembly
assembly {
z := mul(x, y)
// Equivalent to `require(y == 0 || x <= type(uint256).max / y)`.
if iszero(eq(div(z, y), x)) {
if y {
mstore(0x00, 0xbac65e5b) // `MulWadFailed()`.
revert(0x1c, 0x04)
}
}
z := add(iszero(iszero(mod(z, WAD))), div(z, WAD))
}
}
Reference
https://www.rareskills.io/post/solidity-fixed-point
https://github.com/abdk-consulting/abdk-libraries-solidity/blob/master/ABDKMath64x64.sol
https://github.com/transmissions11/solmate/blob/main/src/utils/FixedPointMathLib.sol
https://github.com/Vectorized/solady/blob/main/src/utils/FixedPointMathLib.sol
ERC4626
背景
ERC4626 是一种代币化的份额标准,它使用 ERC20 代币来代表其他资产的份额。
它的工作原理是,你将一个 ERC20 代币(代币 A)存入 ERC4626 合约,并取回另一个 ERC20 代币,称之为代币 S。
在这个例子中,代币 S 代表你在当前合约所拥有的所有代币 A 中的份额(不是 A 的总供应量,只是 ERC4626 合约中 A 的余额)。
稍后,您可以将代币 S 放回合约并取回代币 A。
如果合约中的代币 A 余额增长速度快于代币 S 的生产速度,那么您提取的代币 A 数量将按比例大于您存入的代币 A 数量。
abstract contract ERC4626 is ERC20, IERC4626 {
constructor(IERC20 asset_) {
(bool success, uint8 assetDecimals) = _tryGetAssetDecimals(asset_);
_underlyingDecimals = success ? assetDecimals : 18;
_asset = asset_;
}
}
ERC4626 扩展了 ERC20 合约,在构建阶段,它将其他 ERC20 代币用户将存入的资金作为参数。
因此,ERC4626 支持您期望 ERC20 具有的所有功能和事件: balanceOf transfer transferFrom approve allowance
ERC4626 发行的代币被称为股份,您拥有的股份越多,您对存入其中的基础资产(其他 ERC20 代币)的权利就越大。
每个 ERC4626 合约仅支持一种资产,不支持将多种 ERC20 代币存入合约并取回份额。
ERC4626 动机
让我们用一个真实的例子来激发设计。
假设我们每个人都拥有一家公司或一个流动资金池,定期赚取稳定币 DAI。在这种情况下,稳定币 DAI 就是资产。
分配收益的一种低效方法是按比例将 DAI 分发给公司的每个持有人。但这会非常昂贵。
同样,如果我们要在智能合约中更新每个人的余额,那么成本也会很昂贵。
相反,这是工作流程与 ERC4626 一起工作的方式。
假设您和
9位朋友聚在一起,每人向ERC4626保险库存入10 DAI(总计100 DAI)。您会获得一份股份。到目前为止一切顺利。现在您的公司又赚了
10 DAI,因此保险库内的总DAI现在为110 DAI当您将您的份额换回您的那部分
DAI时,您拿回的不是10 DAI,而是11 DAI。现在保险库里有
99 DAI,但有 9 个人可以分享。如果他们每人提取,每人将获得11 DAI。
请注意这是多么高效。当有人进行交易时,不是逐个更新每个人的股份,而是只有股份的总供应量和合约中的资产数量发生变化。
ERC4626 不局限于这种方式使用。你可以使用任意数学公式来确定股份和资产之间的关系。例如,你可以说每次有人提取资产时,他们还必须支付某种税款,这取决于区块时间戳或类似的东西。
接口详解
自然,用户希望知道 ERC4626 使用了哪种资产以及合约拥有多少资产,因此 ERC4626 规范中有两个solidity函数用于此。
asset() 函数返回用于 Vault 的底层代币的地址。如果底层资产是 DAI,那么该函数将返回 DAI 的 ERC20 合约地址。
totalAssets() 函数用于查询该合约中用于 Vault 的代币总量,调用该函数将返回保险库“管理”(拥有)的资产总额,即 ERC4626 合约拥有的 ERC20 代币数量
/** @dev See {IERC4626-asset}. */
function asset() public view virtual returns (address) {
return address(_asset);
}
/** @dev See {IERC4626-totalAssets}. */
function totalAssets() public view virtual returns (uint256) {
return IERC20(asset()).balanceOf(address(this));
}
存入资产,获取股份:deposit() 和 mint()
// EIP: Mints a calculated number of vault shares to receiver by depositing an exact number of underlying asset tokens, specified by user.
function deposit(uint256 assets, address receiver) public virtual override returns (uint256)
// EIP: Mints exact number of vault shares to receiver, as specified by user, by calculating number of required shares of underlying asset.
function mint(uint256 shares, address receiver) public virtual override returns (uint256)
用户存入的是资产,拿回的是份额,那么这两个功能到底有什么区别呢?
- deposit(),指定要投入多少资产,然后该函数将计算要向您发送多少股份。
- 指定您想要交易的资产,合约会计算您获得多少股份。
- mint(),指定所需的股份数,然后该函数将计算要从您那里转移多少
ERC20资产。- 当然,如果您没有足够的资产转入合同,交易将会撤销。
- 指定想要多少股份,合约会计算从您那里拿走多少资产
预测在理想情况下您存入资产后,将获得多少股份, previewDeposit 它将资产作为参数并返回在理想条件下(无滑点或费用)您将获得的股票数量。
/** @dev See {IERC4626-previewDeposit}. */
function previewDeposit(uint256 assets) public view virtual returns (uint256) {
return _convertToShares(assets, Math.Rounding.Floor);
}
预测在理想情况下获得预期的股份,需要存入的 ERC20 数量, previewMint 它将资份额作为参数并返回在理想条件下(无滑点或费用)您需要存入的 ERC20 代币数量。
/** @dev See {IERC4626-previewMint}. */
function previewMint(uint256 shares) public view virtual returns (uint256) {
return _convertToAssets(shares, Math.Rounding.Ceil);
}
预测在理想情况下退款预期份额,将获得多少资产, previewRedeem 它将份额作为参数并返回在理想条件下(无滑点或费用)您将获得的 ERC20 数量。
/** @dev See {IERC4626-previewRedeem}. */
function previewRedeem(uint256 shares) public view virtual returns (uint256) {
return _convertToAssets(shares, Math.Rounding.Floor);
}
预测在理想情况下获得预期的 ERC20 代币数量,需要退回的份额数量, previewWithdraw 它将资份额作为参数并返回在理想条件下(无滑点或费用)您需要存入的 ERC20 代币数量。
/** @dev See {IERC4626-previewWithdraw}. */
function previewWithdraw(uint256 assets) public view virtual returns (uint256) {
return _convertToShares(assets, Math.Rounding.Ceil);
}
mint、deposit、redeem 和 withdraw 函数有第二个参数“receiver”,用于接收来自 ERC4626 的股票或资产的账户不是的情况 msg.sender 。
这意味着我可以将资产存入账户,并指定 ERC4626 合约给你股票。
滑点
任何代币兑换交换协议都存在一个问题,即用户可能无法取回他们期望的资产数量。
例如,对于自动做市商来说,大额交易可能会耗尽流动性并导致价格大幅波动。
另一个问题是交易被抢先交易或遭遇夹层攻击。在上面的例子中,我们假设 ERC4626 合约无论供应量如何,都保持资产和股票之间的一对一关系,但 ERC4626 标准并未规定定价算法应如何工作。
例如,假设我们将发行的股票数量设为存入资产的平方根的函数。在这种情况下,谁先存入,谁就能获得更多的股票。这可能会鼓励投机取巧的交易者抢先存入订单,并迫使下一位买家为相同数量的股票支付更多的资产。
对此的防御很简单:与 ERC4626 交互的合约应该测量其在存款期间收到的股份数量(以及取款期间的资产数量),如果在一定的滑点容忍度内没有收到预期的数量,则应恢复。
这是处理滑动问题的标准设计模式,防御有三种:
如果收到的金额不在滑点容忍范围内(前面已描述),则撤销
部署者应该向池中存入足够多的资产,这样进行通胀攻击的成本就会太高
向金库添加“虚拟流动性”,以便定价就像池子里部署了足够的资产一样。`
虚拟流动性
在计算存款人收到的股份数量时,总供应量会被人为地夸大(按照程序员在 中指定的比率 _decimalsOffset())。
让我们来看一个例子。提醒一下,上面的变量的含义如下:
- totalSupply() = 已发行股票总数
- totalAssets()= ERC4626 持有资产余额
- 资产 = 用户存入的资产数量
shares_received = assets_deposited * totalSupply() / totalAssets();
假设我们有以下数字:
assets_deposited= 1,000
totalSupply()= 1,000
totalAssets()= 999,999(公式加 1,因此我们将这样设置以使数字好看)
在这种情况下,用户将获得的份额是1000 * 1000 / 1000000 = 1。
这显然是非常脆弱的,如果攻击者抢先押注 1000 股并存入资产,那么受害者将得到 1000 * 1000 / (1000000+1000) = 0,因为在整数除法中,100 万除以大于 100 万的数字是零。
function _convertToShares(uint256 assets, Math.Rounding rounding) internal view virtual returns (uint256) {
return assets.mulDiv(totalSupply() + 10 ** _decimalsOffset(), totalAssets() + 1, rounding);
}
虚拟流动性如何解决这个问题?使用上面的代码,我们将其设置 _decimalOffset() = 3,这样就会 totalSupply() 将 1,000 添加到其中。
实际上,我们将分子放大了 1,000 倍。这迫使攻击者捐款 1,000 倍,从而打消了他们进行攻击的念头。
引用
完整继承 ERC4626 的实现代码:
// SPDX-License-Identifier: MIT
pragma solidity 0.8.20;
import "@openzeppelin/contracts/token/ERC20/extensions/ERC4626.sol";
import "@openzeppelin/contracts/token/ERC20/IERC20.sol";
import "@openzeppelin/contracts/token/ERC20/ERC20.sol";
contract MyVault is ERC4626 {
constructor(
IERC20 asserts,
string memory name,
string memory symbol
) ERC4626(asserts) ERC20(name, symbol) {}
}
闪电贷
闪电贷是智能合约之间的借贷,必须在同一笔交易中偿还。本文介绍了 ERC3156 闪电贷规范以及闪电贷出方和借款方可能遭受黑客攻击的方式。最后提供了建议的安全练习。
以下是一个极其简单的闪电贷示例。

如果借款人不偿还贷款,则带有“闪付未还”信息的要求声明将导致整个交易撤销。
只有合约才能与闪电贷合作
EOA 钱包无法调用 flashloan() 函数来获取闪电贷,然后在单笔交易中将代币转回。与闪电贷的集成需要单独的智能合约。
闪电贷无需抵押
如果闪电贷能够得到妥善实施,那么就不存在贷款无法偿还的风险,因为一个 revert 或失败的 require 语句都会导致交易失败,代币就不会转移。
闪电贷有何用途?
套利
闪电贷最常见的用例是进行套利交易。
例如,如果以太币在一个池子里的交易价格为 1,200 美元,而在另一个 DeFi 应用程序中的交易价格为 1,300 美元,那么最好在第一个池子里购买以太币,然后在第二个池子里卖掉,赚取100美元的利润。但是,你首先需要钱来购买以太币。闪电贷是理想的解决方案,因为你不需要闲置1,200美元。你可以借入1,200美元的以太币,以 1,300美元的价格卖掉,然后偿还1,200美元,为自己保留100美元的利润(减去费用)。
再融资贷款
对于常规的 DeFi 贷款,它们通常需要某种形式的抵押品。例如,如果您借入 10,000 美元的稳定币,则需要存入 15,000 美元的以太币作为抵押品。
如果你的稳定币贷款利率为 5%,而你想用另一个利率为 4% 的贷款智能合约进行再融资,你需要
用稳定币偿还 10,000 美元
提取 15,000 美元的以太币抵押品
将 15,000 美元的以太币抵押品存入另一个协议
以较低的利率再次借入 10,000 美元的稳定币
如果您将 10,000 美元用于其他应用程序,那么这将有问题。使用闪电贷,您可以执行步骤 1-4,而无需使用任何自己的稳定币。
交换抵押品
在上面的例子中,借款人使用 15,000 美元的以太币作为抵押品。但假设该协议使用 wBTC(包装比特币)提供较低的抵押率?借款人可以使用闪电贷和上面概述的类似步骤来换出抵押品而不是本金。
清算借款人
在 DeFi 贷款的背景下,如果抵押品跌破某个阈值,那么抵押品就会被清算——强制出售以支付贷款成本。
在上面的例子中,如果以太币的价值跌至
12,000美元,那么协议可能会允许某人以11,500美元的价格购买以太币,前提是他们先偿还10,000美元的贷款。清算人可以使用闪电贷来偿还
10,000美元的稳定币贷款,并用11,500美元的价格购入以太币。然后他们会在另一个交易所将其出售以获得稳定币,然后偿还闪电贷。
在单笔交易中构建杠杆循环
通过使用借贷协议,人们可以实现杠杆多头和空头。
例如,要杠杆做多 ETH,用户可以将 ETH 作为抵押品存入借贷池,借入稳定币,然后将稳定币换成 ETH,然后将 ETH 存入借贷池并不断重复该过程。 抵押品和借入 ETH 的总规模将大于原始金额,从而使借款人能够更多地参与 ETH 的价格。
要利用杠杆做空 ETH,用户可以将稳定币存入借贷池,借入 ETH,将 ETH 换成稳定币,然后将稳定币存入借贷池并不断重复该过程。现在用户有大量 ETH 债务,如果 ETH 价格下跌,偿还起来会更容易。
以这种方式可以借入的资产总额为
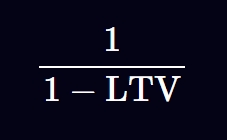
LTV 是协议将接受的最大贷款价值比。
例如,如果协议要求存入价值 1000 美元的稳定币才能借入 800 美元的 ETH,那么 LTV 就是 800/1000 = 0.8
你可以
使用闪电贷借入价值 5,000 美元的稳定币
将稳定币兑换为价值 5,000美元的 ETH
将 ETH 放入借贷池作为抵押品
从借贷池借入价值 4,000美元的稳定币
用他们从借贷池中借入的 4,000美元稳定币加上他们自己的 1,000美元稳定币,偿还闪电贷。
现在用户拥有价值 5,000美元的 ETH 作为抵押品
也就是说,用户可以用 1000美元的存款敞口投资价值 5000美元的 ETH 。
破解智能合约
闪电贷最出名的可能是被黑帽黑客用来利用协议。
闪电贷的主要攻击媒介是价格操纵和治理(投票)操纵。在防御不足的 DeFi 应用程序上使用,闪电贷允许攻击者大量购买资产以提高其价格,或获取大量投票代币以推动治理提案。
ERC3156 闪电贷 协议
ERC3156 旨在标准化闪电贷的接口
ERC3156 Borrower
标准第一点是借款人需要实现的接口,如下所示,借款人只需要实现一个函数即可:
// SPDX-License-Identifier: MIT
// OpenZeppelin Contracts (last updated v5.1.0) (interfaces/IERC3156FlashBorrower.sol)
pragma solidity ^0.8.20;
/**
* @dev Interface of the ERC-3156 FlashBorrower, as defined in
* https://eips.ethereum.org/EIPS/eip-3156[ERC-3156].
*/
interface IERC3156FlashBorrower {
/**
* @dev Receive a flash loan.
* @param initiator The initiator of the loan.
* @param token The loan currency.
* @param amount The amount of tokens lent.
* @param fee The additional amount of tokens to repay.
* @param data Arbitrary data structure, intended to contain user-defined parameters.
* @return The keccak256 hash of "ERC3156FlashBorrower.onFlashLoan"
*/
function onFlashLoan(
address initiator,
address token,
uint256 amount,
uint256 fee,
bytes calldata data
) external returns (bytes32);
}
initiator
构造借贷交易的地址,应该就是本合约的地址,应该再合约内部执行校验。
onFlashLoan() 因为该函数是 external 修饰,任何人都可以调用它,因此需要保证该函数不会被恶意调用。
如果不判断
initiator == address(this)的话任何地址可以直接调用 lender 合约的 flashloan() 函数
将该
borrower作为 receiver 参数
Flashloan()将会在每次被调用的时候,收入borrower合约的手续费最终榨干
borrower的余额
令牌
这是您要借入的 ERC20 代币的地址。提供闪电贷的合约通常会持有多个可以闪电贷出的代币。ERC3156 闪电贷标准不支持闪电贷出原生 Ether,但这可以通过闪电贷出 WETH 并让借款人解开 WETH 来实现。由于借款合约不一定是调用闪电贷出者的合约,因此可能需要告知借款合约正在闪电贷出哪种代币。
费用
费用是需要支付多少代币作为借贷费用。它以绝对金额表示,而不是百分比。
数据
如果您的闪电贷接收合约没有硬编码为在接收闪电贷时采取特定操作,则您可以使用 data 参数来参数化其行为。例如,如果您的合约是套利交易池,那么您可以指定与哪些池进行交易。
返回值
调用最终应该返回 keccak256("ERC3156FlashBorrower.onFlashLoan")
ERC3156 Borrower 实施方案
这已从 ERC3156 规范中的代码进行了修改,以使代码片段更小。请注意,此合约仍然完全信任闪电借出方。如果闪电借出方以某种方式受到损害,则可以通过向其提供虚假数据来利用以下合约
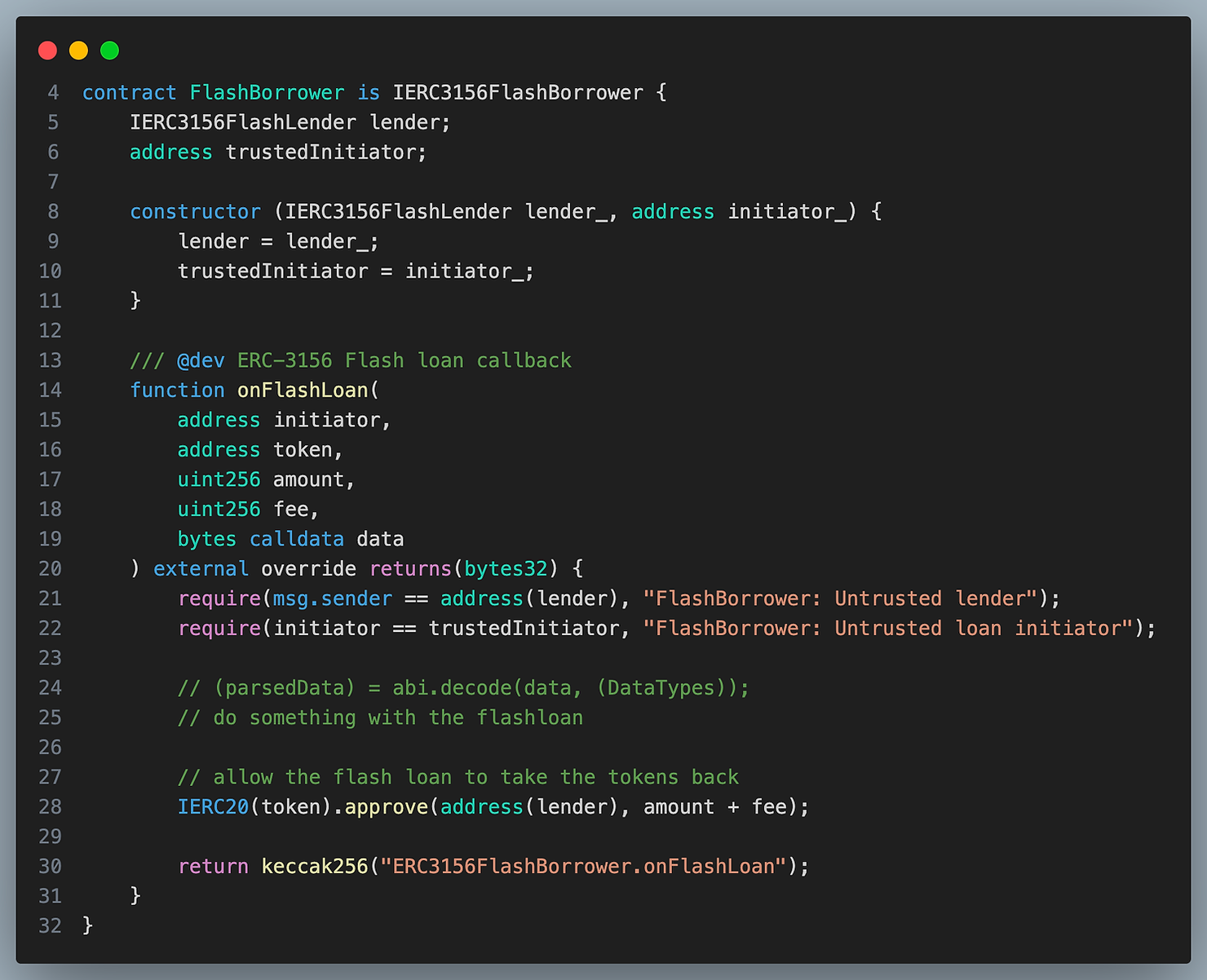
ERC3156 Lender
标准规范
// SPDX-License-Identifier: MIT
// OpenZeppelin Contracts (last updated v5.1.0) (interfaces/IERC3156FlashLender.sol)
pragma solidity ^0.8.20;
import {IERC3156FlashBorrower} from "./IERC3156FlashBorrower.sol";
/**
* @dev Interface of the ERC-3156 FlashLender, as defined in
* https://eips.ethereum.org/EIPS/eip-3156[ERC-3156].
*/
interface IERC3156FlashLender {
/**
* @dev The amount of currency available to be lended.
* @param token The loan currency.
* @return The amount of `token` that can be borrowed.
*/
function maxFlashLoan(address token) external view returns (uint256);
/**
* @dev The fee to be charged for a given loan.
* @param token The loan currency.
* @param amount The amount of tokens lent.
* @return The amount of `token` to be charged for the loan, on top of the returned principal.
*/
function flashFee(address token, uint256 amount) external view returns (uint256);
/**
* @dev Initiate a flash loan.
* @param receiver The receiver of the tokens in the loan, and the receiver of the callback.
* @param token The loan currency.
* @param amount The amount of tokens lent.
* @param data Arbitrary data structure, intended to contain user-defined parameters.
*/
function flashLoan(
IERC3156FlashBorrower receiver,
address token,
uint256 amount,
bytes calldata data
) external returns (bool);
}
该 flashLoan() 函数需要完成几个重要的操作:
有人可能会 flashLoan() 使用闪电贷合约不支持的代币进行调用。应检查这一点。
有人可能会 flashLoan() 跟注金额大于 maxFlashLoan。 这也应该检查
data 只是转发给 caller 执行。
更重要的是,flashLoan() 必须将代币转给接收者,然后再转回。
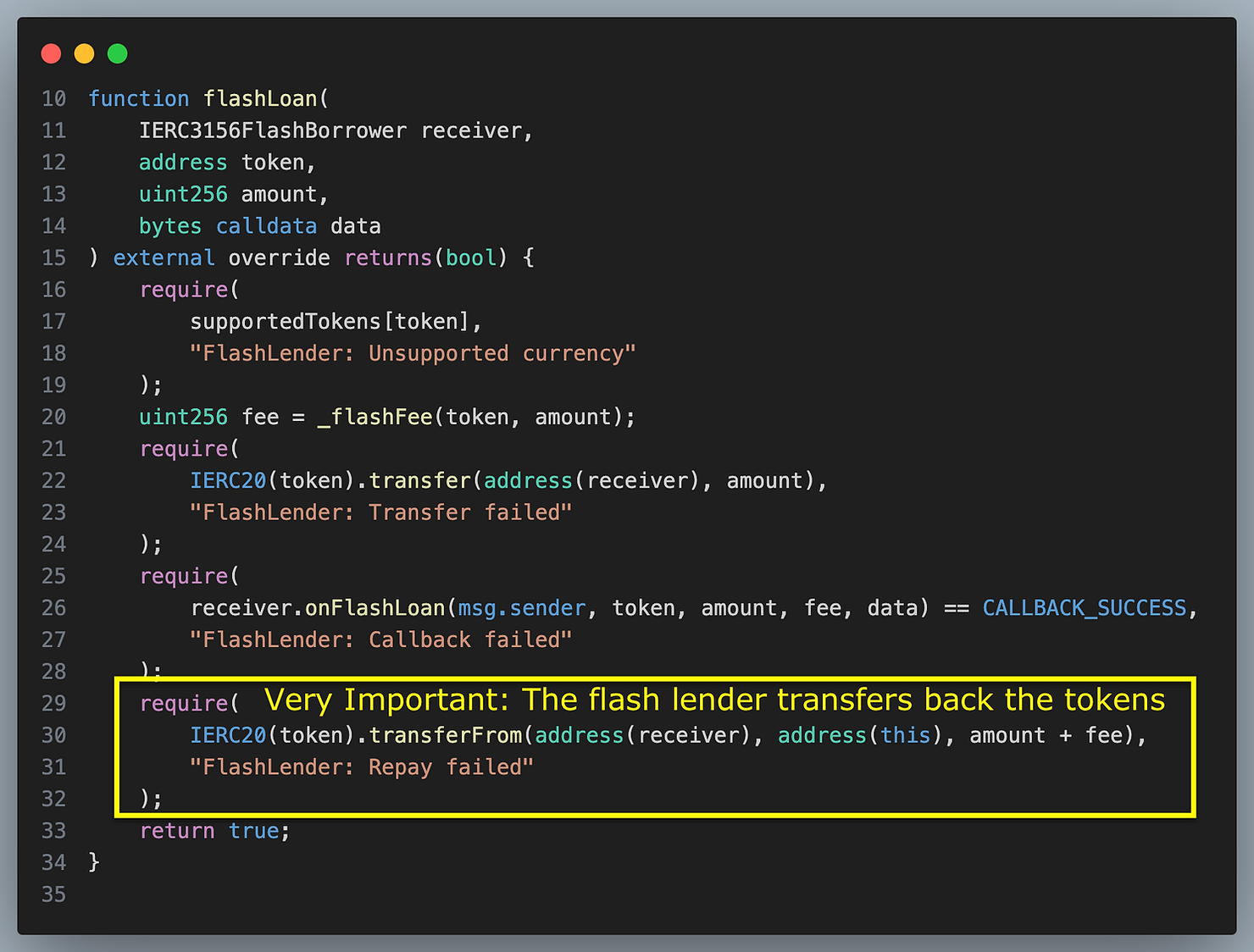
请注意,参考实现假设 ERC20 代币在成功时返回 true,但并非所有代币都如此,因此如果使用不兼容的 ERC20 代币,请使用 SafeTransfer 库。
安全注意事项
Borrower的访问控制和输入验证
Borrower 贷款合约必须有控制措施,只允许 lender 借款合约调用 onFlashLoan()
否则,其余参与者也可以调用 onFlashLoan() 并导致意外行为。
此外,再lender 借款合约中,任何人都可以调用 flashloan()函数,任意指定 Borrower 贷款合约并传递任意数据。为了确保数据不是恶意的,闪电贷接收方合约应该只允许一组有限的调用者地址。
重入锁非常重要
ERC3156 从定义上来说不能遵循检查效果模式来防止重入。它必须通知借款人它已经收到了代币(进行外部调用),然后将代币转回。因此,nonReentrant 应该在合约中添加锁定。
将借出代币转回
Lender 借款合约应该在确认Borrower贷款地址收到代币并执行一系列逻辑后,将代币转回借款合约
贷方将代币从借方转回,借方并不会主动将代币转回。
在使用 balanceOf(address(this)) 进行判断代币是否回流的时候,这对于避免“侧入”很重要,即借方以贷方的身份将钱存入协议。现在,资金池看到其余额已恢复到以前的水平,但借方突然变成了拥有大量存款的贷方。
UniswapV2 的闪电贷在贷款结束后不会将代币转回。但是,它使用重入锁来确保借款人不能像贷款人一样将贷款存回协议来“偿还贷款”。
确保onFlashLoan调用的交易发起者是 borrower合约地址
Lender闪电贷款人地址被硬编码为仅调用接收方的 onFlashLoan() 函数而不调用其他函数。
如果借款人有办法指定闪电贷款人将调用哪个函数,那么闪电贷款就可以被操纵,将其持有的其他代币转移(通过调用ERC20.transfer)或批准将其代币余额转移到恶意地址。
因为这样的操作需要明确调用 ERC20transfer 或 approve,所以如果闪电贷出者只能调用,这种情况就不会发生 onFlashLoan()。
使用 token.balanceOf(address(this)) 可以进行操作
在上面的实现中,我们没有使用 balanceOf(address(this)) 来确定最大闪电贷规模。
其他人可以直接将代币转移到合约中,从而干扰逻辑,从而改变这一点。
我们知道闪电贷已偿还的方式是因为贷方将贷款金额 + 费用转回。
有效的方法来 balanceOf(address(this)) 检查还款情况,但这必须与重入检查相结合,以避免将贷款作为押金偿还。
为什么闪电借款人需要返回 keccak256(“ERC3156FlashBorrower.onFlashLoan”);
这处理了 Borrower 合约不存在 onFlashLoan() 函数,仅仅在 fallback() 中执行批准闪电贷出合约的情况。有人可以反复以该合约为接收者发起闪电贷。然后会发生以下情况:
受害合约获得闪电贷
受害者合约被调用onFlashLoan(),但是仅触发 fallback 函数。
闪电贷出方从借款方提取代币+手续费
如果此操作循环发生,则具有 fallback() 功能的受害合约将被耗尽。 EOA 钱包也可能发生同样的情况,因为使用 onFlashLoan 调用钱包地址不会 revert。
仅检查函数 onFlashLoan 是否 revert 是不够的。闪电借出方还会检查返回值 keccack256("ERC3156FlashBorrower.onFlashLoan") 是否已返还,以便了解借款人是否打算借入代币并偿还费用。
交易市场简介
中心化交易所(CEX)如何工作
首先一个运行在以太坊(Ethereum)上的去中心化交易所(DEX)。
DEX 的设计模式非常复杂多样,因此我们先来考虑中心化交易所的设计。中心化交易所(CEX)的核心为订单簿(order book),它存储了用户的所有买单和卖单。订单簿中的每一笔订单都包含了订单成交的价格以及成交数量。
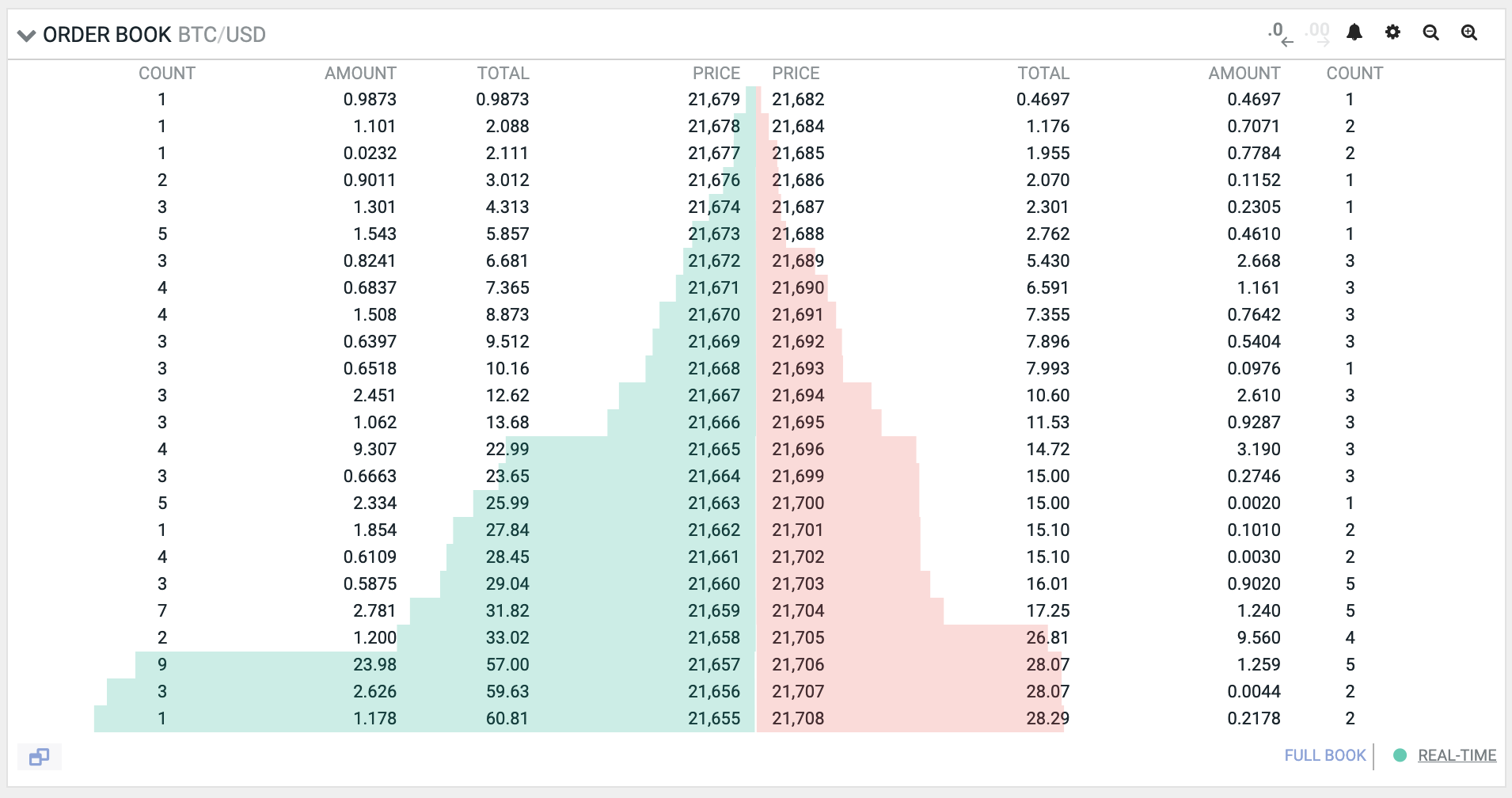
交易能够正常进行的保障是流动性(liquidity),也即整个市场中所有可用的资产数目。
假设你希望购买一个衣柜但是没有人售卖,即为没有流动性;如果你希望卖出一个衣柜但是没有人愿意购买,即为市场有流动性但是没有买方。没有流动性,就无法在市场中进行买卖。
在 CEX 中,流动性存放在订单簿里。如果某个用户提交了一个卖单,他就为市场提供了流动性;如果某人提交了一个买单,他希望市场有流动性,否则交易就无法进行。
如果市场缺乏流动性,但是交易者仍然希望进行交易,那么就需要做市商(market maker)。做市商是向市场提供流动性的、拥有大量各种资产的公司或个人。通过提供流动性,做市商能够从交易中获取利润。
去中心化交易所(DEX)如何工作
毫无疑问,去中心化的交易也需要流动性,并且也需要做市商向市场提供多种资产的流动性。然而,在 DEX 中这个过程无法被中心化地处理,我们需要一种去中心化的做市商方案。相关解决方案非常多样化,而本书将主要关注 Uniswap 提供的方案。
自动做市商(AMM)
链上交易市场的历史 一文提到了一种称作自动做市商(Automated Market Maker)的思路。正如其名,这种算法能够自动化完成像做市商一样的工作。更进一步,这种算法是去中心化且无需许可的,也即:
- 没有被任何单个中心化机构控制
- 所有资产并不存储在同一地方
- 任何人在任何地点都能使用
什么是自动做市商AMM?
一个 AMM 是一套定义如何管理流动性的智能合约。每个单独的交易对(例如 ETH/USDC)都是一个单独的智能合约,它存储了 ETH 和 Token 的资产并且撮合交易。在这个合约中,我们可以将 ETH 兑换成 USDC 或者将 USDC 兑换成 ETH。
在 AMM 中,一个核心概念为池子(pooling):每个合约都是一个存储流动性的池子,允许不同的用户(包括其他合约)在其中进行某种方式的交易。AMM 中有两种角色,*流动性提供者(LP)*以及交易者(trader);这两方通过流动性池进行交互,而交互的方式由合约进行规定且不可更改。
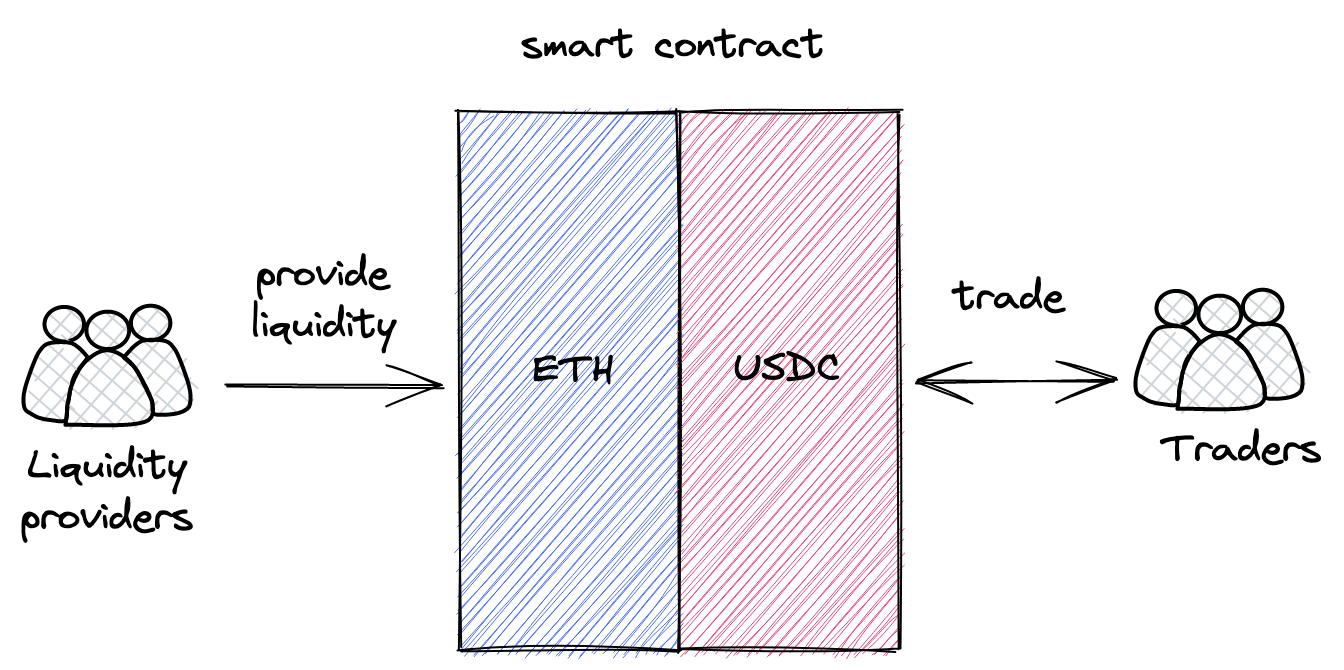
这种交易方法与 CEX 的关键区别在于: 智能合约是完全自动化并且不受任何人控制的。没有经理,没有系统管理员,没有特权用户,一切都没有。这里只有 LP 和交易者,任何人都可以担任这两种角色(也可以同时),并且所有的算法都是公开的、程序规定的、不可更改的。
恒定函数做市商 (Constant Function Market Makers)
本章节主要讲述了 Uniswap 白皮书中的内容. 理解其中的数学原理能帮助你更好地构建像 Uniswap 这样的应用
正如我们在上一节中提到的那样,AMM 的构建有许多不同的方法。我们将主要关注与构建一种特定的 AMM:恒定函数做市商(有时也被称为恒定乘积做市商)。尽管名字听起来很复杂,但是它的核心数学原理只是一个非常简单的公式:
$$x * y = k$$
仅此而已,这就是 AMM.
$x$ 和 $y$ 是池子合约所拥有的两种资产的数目。$k$ 是它们的乘积,我们暂时不考虑它的实际值等于多少。
为什么只有两种资产x和y? 每个 Uniswap 的池子仅包含两种 资产。我们使用 x 和 y 来表示一个池子中的两种资产,其中 x 代表第一个 token,y 代表第二个 token。两种 token 的顺序(暂时)并不重要。
恒定函数做市商的原理是:在每次 swap 交易后,k 必须保持增加或不变。当用户进行交易,他们通常将一种类型的 token 放入池子(也即他们打算卖出的 token ),并且将另一种类型的 token 移出池子(也即打算购买的 token)。这笔交易会改变池子中两种资产的数量,而上述原理表示,两种资产数目的乘积必须保持不变。我们之后还会在本书中看到许多次这个原理,这就是 Uniswap 的核心机制。
AMM 自动做市商合约内部持有交易对,允许交易对代币之间互相兑换,需要注意的是每次交易兑换都会收取相应的手续费,因此,每笔交易都会推高 k 值:
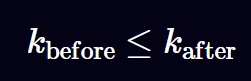
展开上面的方程,我们得到下面的等效方程:
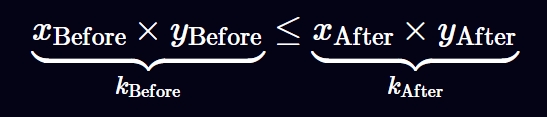
下面我们来看一个更加具体的例子:
- 起始价格为
50(10 ETH = 500 OMG), - 我们卖出
1个ETH,手续费收取 3 % - 如果我们仅以现货价格计算,计算能够获得的
OMG
- 往池子中注入的ETH数量为:
1 *(1-3%) - 注入 ETH 后,池子的ETH代币数量为:
10 + 1*(1-3%) - 10 * 500 <= (10 + 1*(1-3%))* (500 - dy)
- dy <= 44.21,交易实际发生的价格是
44.21
- 交易完成后:
- 交易池子中新增
1 ETH, 总量为10 + 1 = 11 ETH - 交易池子中减少
44.21 OMG,总量为500 - 44.21 = 455.79 OMG - 兑换后后池子总流动性为:
11 * 455.79 = 5013.69 > 5000
因此,由于收续费的原因,每次兑换都会推高总流动性的值,早期提供流动性代币的用户就会获利
交易函数
现在我们知道了什么是池子以及交易的原理,接下来我们写一下交易发生时的公式:
(x + r $\Delta x$)(y - $\Delta y$) >= k, r表示手续费
- 一个池子包含一定数量的
token0($x$) 和一定数量的token1($y$) - 当我们用
token0购买token1的时候,一些token0被放入池子 ($\Delta x$) - 这个池子将给我们一定数量的
token1作为交换 ($\Delta y$) - 池子也会从我们给出的
token0中收取一定数量的手续费 ($r$) - 池子中
token0的数量发生了变化 ($x + r \Delta x$),token1的数量也发生了变化 ($y - \Delta y$) - 二者的乘积保持 >= $k$
我们使用 token0 和 token1 这样的表述,是为了与代码保持一致。现在,两个 token 的顺序并不重要。
简单来说,我们给了池子一定数量的 token0,然后获得了一定数量的 token1。这个池子的工作就是按照一个合理的价格,给予我们正确数量的 token1。我们可以得出以下结论:池子决定了交易的价格。
价格
池子里 token 的价格是如何计算的?
由于 Uniswap 不同的池子对应不同的智能合约,同一个池子里的两种 token 互为计价标准进行定价。例如:在一个 ETH/USDC 的池子里,ETH 的价格用 USDC 作为标定,而 USDC 的价格用 ETH 作为标定。假设一个 ETH 的价格是1000 USDC,那么一个 USDC 的价格就是 0.001 ETH。每一个池子都是如此,无论 token 是否为稳定币(例如,ETH/BTC 池)
在现实世界中,价格是根据供求关系来决定的,对于 AMM 当然也是如此,现在,我们先不考虑需求方,只关注供给方。
池子中 token 的价格是由 token 的供给量决定的,也即池子中拥有该 token 的资产数目。token 的价格公式如下:
$$P_x = \frac{y}{x}, \quad P_y=\frac{x}{y}$$
其中 $P_x$ 和 $P_y$ 是一个 token 相对于另一个 token 的价格
这个价格被称作 现货价格/现价, 它反映了当前的市场价。然而,交易实际成交的价格却并不是这个价格。现在我们再重新把需求方纳入考虑:
根据供求关系,需求越高,价格越高,这也是我们应当在去中心化交易中满足的性质。我们希望当需求很高的时候价格会升高,并且我们能够用池子里的资产数量来衡量需求:你希望从池子中获取某个token的数量越多,价格变动就越剧烈。我们再重新考虑上面这个公式:
(x + r $\Delta x$)(y - $\Delta y$) = xy
从这个公式中,我们能够推导出关于 $\Delta x$ 和 $\Delta y$ 的式子,这也意味着我们能够通过交易付出的 token 数目来计算出获得的 token 数目,反之亦然:
$$\Delta y = \frac{y r \Delta x}{x + r \Delta x}$$ $$\Delta x = \frac{x \Delta y}{r(y - \Delta y)}$$
这些公式就能够让我们重新计算价格。我们能够从 $\Delta y$ 公式中求出获得 token 数量(当我们希望卖出 token 的数量为定值),并且从 $\Delta x$ 的公式中求出需要提供的 token 数量(当我们购买 token 的数量为定值)。注意到,这里的公式是资产之间的关系,同时也把交易的数量(第一个公式中的 $\Delta x$ 和第二个公式中的 $\Delta y$)加入了计算。这是同时考虑了供求双方的价格函数。事实上,我们甚至并不需要去计算价格!(因为我们直接计算出了交易的结果)
下面是从交易函数推导出上述价格函数的过程: $$(x + r\Delta x)(y - \Delta y) = xy$$
$$y - \Delta y = \frac{xy}{x + r\Delta x}$$
$$-\Delta y = \frac{xy}{x + r\Delta x} - y$$
$$-\Delta y = \frac{xy - y({x + r\Delta x})}{x + r\Delta x}$$
$$-\Delta y = \frac{xy - xy - y r \Delta x}{x + r\Delta x}$$
$$-\Delta y = \frac{- y r \Delta x}{x + r\Delta x}$$
$$\Delta y = \frac{y r \Delta x}{x + r\Delta x}$$ 以及: $$(x + r\Delta x)(y - \Delta y) = xy$$
$$x + r\Delta x = \frac{xy}{y - \Delta y}$$
$$r\Delta x = \frac{xy}{y - \Delta y} - x$$
$$r\Delta x = \frac{xy - x(y - \Delta y)}{y - \Delta y}$$
$$r\Delta x = \frac{xy - xy + x \Delta y}{y - \Delta y}$$
$$r\Delta x = \frac{x \Delta y}{y - \Delta y}$$
$$\Delta x = \frac{x \Delta y}{r(y - \Delta y)}$$
曲线
上面的数学计算可能有些抽象和枯燥,下面我们来把恒定乘积函数进行可视化来更好地理解其工作原理
恒定成绩函数的图像为二次双曲线:

横纵轴分别表示池子中两种代币的数量。每一笔交易的起始点都是曲线上与当前两种代币比例相对应的点。为了计算交易获得的 token 数量,我们需要找到曲线上的一个新的点,其横坐标值为 $x+\Delta x$,也即池子中现在 token0 的数量加上我们卖出的数量。y 轴上的变化量就是我们将会获得的 token1 的数量。
下面我们来看一个更加具体的例子:
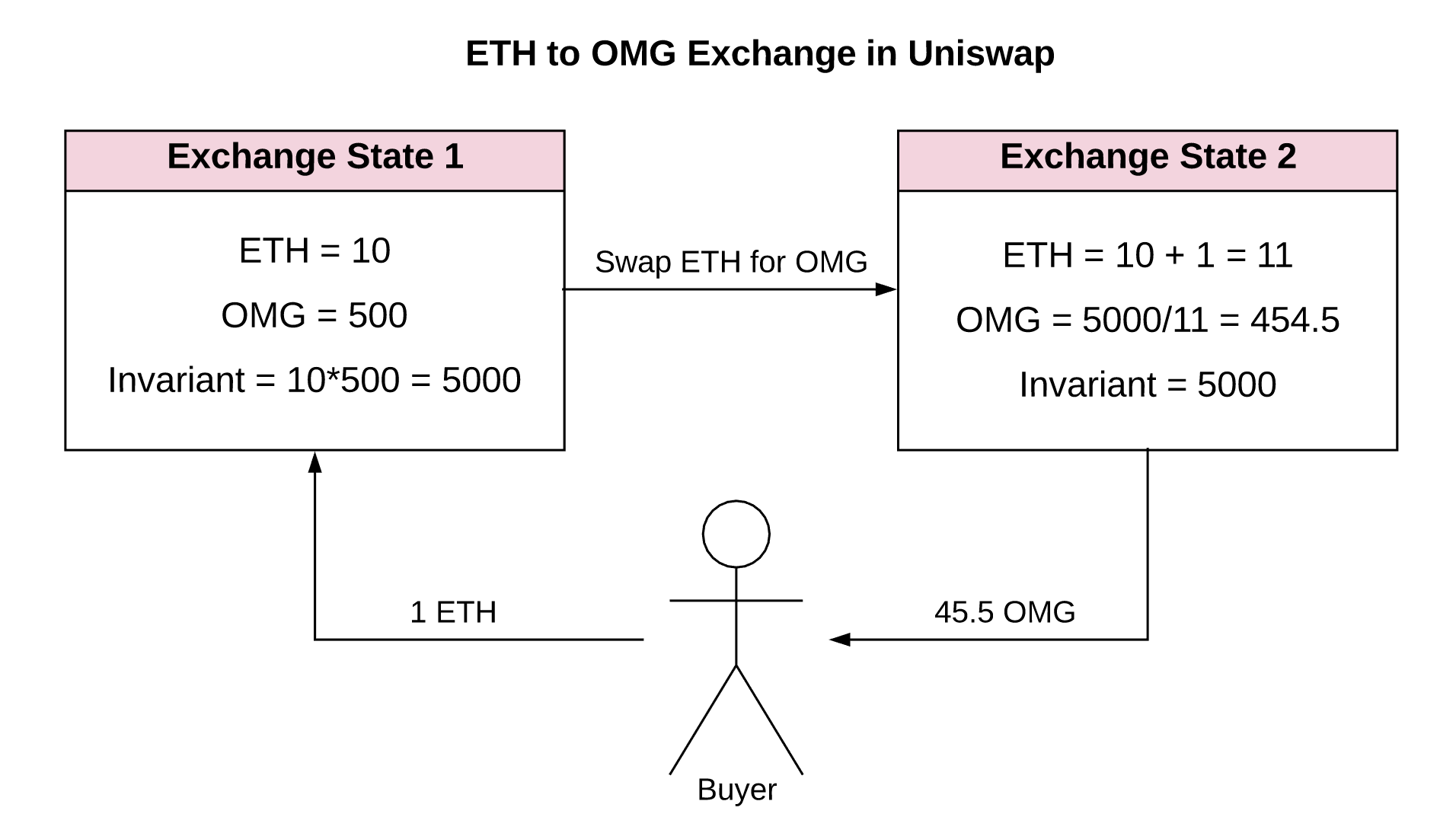
- 紫色的线是公式代表的双曲线,横纵坐标轴代表池子中代币资产的数目(注意到在一开始,两种代币的数量相等)
- 起始价格为
50(1 ETH = 50 OMG) - 我们卖出
1个ETH,如果我们仅以现货价格计算,我们希望获得50个OMG。 - 然而,交易实际发生的价格是
45.5,所以我们仅仅获得了45.5个OMG!
这个例子来源于the Desmos chart,作者是Dan Robinson,
Uniswap 的创始人之一。 为了能够更直观地理解它是如何工作的,你可以尝试自己构建不同的场景并且在图上画出来。试一试不同的资产数目,观察当 $\Delta x$ 远小于 $x$ 时获得代币的数量。
一个很传奇的故事是,Uniswap 就是在 Desmos 中发明出来的.
你或许在想,为什么要用这样的一个曲线?这个曲线看起来好像是在惩罚大额交易者。事实上,的确就是如此,并且这也是一个非常好的性质!供求关系告诉我们,当需求很高的时候(假设供给保持不变),价格也同样很高;当需求低的时候,价格也仍然很低。这正是市场的工作原理。并且很神奇地是,这样一个恒定乘积函数恰好实现了这个机制!需求就是你希望购买 token 的数量,而供给就是池子中的资产。当你希望购买的数量占池子的一个很大比例,价格就会比你购买小数量时更高。这样一个简单的公式,恰恰保证了这么一个强大的机制。
尽管 Uniswap 并不计算交易价格,我们仍然能够从曲线上看到它。事实上,在一笔交易中我们有很多个价格:
- 在交易前,有一个现货价格。这个价格等于池子中两种资产的比例,$y/x$ 或者 $x/y$,取决于你交易的方向。这个价格也是起始点切线的斜率。
- 在交易后,有一个新的现货价格,在曲线上另一个不同的点。这个价格是新的点的切线斜率。
- 这个交易的实际发生价格,是连接新旧点的这条线的斜率。
这就是 UniswapV1/V2 里用到的全部数学!
价格操纵
去中心化借贷
借贷存在两方:lender 和 borrower, lender 借出资产,borrower 提供质押物品借出所需资产
比如 lender 借出 10ETH,那么要求 borrower 质押价值 15ETH 的代币, 核心在于如何确定 borrower 提供的质押物的价值
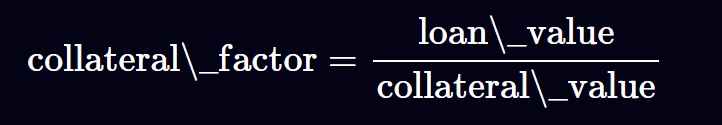
在去中心的借贷网络中,lender 由智能合约充当,数据只能在链上交互,无法和链下真实环境的数据进行交互,因此专门存在和链下数据交互的服务:Oracle语言机
oracle 预言机表现为链上智能合约,通过抛出事件和定时上传数据的方式保持链下通讯,按照数据源-通常分为:
- 链下中心化预言机
- 链下去中心化预言机
- 预言机合约的价格数据源于链下,数据由多方管控
- 预言机合约需要保证数据的快速迭代更新,因此,更新价格的函数权限,通常由
multi-sig控制数,确保数据源的多样性 - Examples:Maker
- 链上中心化预言机
- 链上去中心化预言机
- 预言机合约的价格数据源于链上,通常从
DEX中获取实时价格 - 任何人都可以更新预言机合约中的实时价格数据(存在机制保障价格不会过度浮动)
- 预言机合约的价格数据源于链上,通常从
- 常量预言机
- 预言机合约数据存储价格常量,通常作为稳定币的价格锚点
问题分析
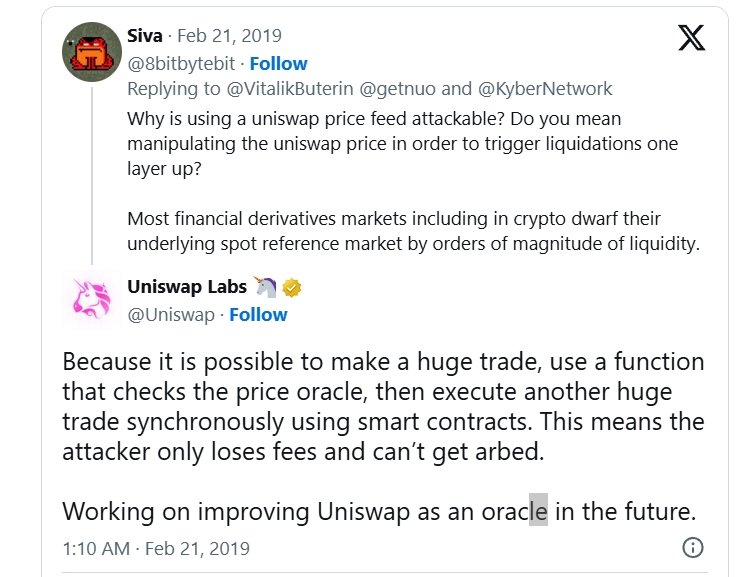
基于公式 (x + r $\Delta x$)(y - $\Delta y$) = xy 的 AMM 在遇到大额兑换单的时候,会猛然提高交易对中 token1 的价值,造成获利(三明治夹子原理)
解决方案
- 使用链上去中心化预言机获取价格的话,需要制定价格区间滑点,防止价格过度波动
Reference
https://www.rareskills.io/post/defi-liquidations-collateral
https://samczsun.com/taking-undercollateralized-loans-for-fun-and-for-profit/
Uniswap V1
- 仅支持创建
ETH-Token的交易对 - 同个交易池中只能进行
ETH/Token的兑换 - 不同
Token的兑换,需要不同交易池的参与
@public
def createExchange(token: address) -> address:
assert token != ZERO_ADDRESS
assert self.exchangeTemplate != ZERO_ADDRESS
// 当前Token未创建过交易池
assert self.token_to_exchange[token] == ZERO_ADDRESS
// 创建交易池
exchange: address = create_with_code_of(self.exchangeTemplate)
// 记录交易对合约地址
Exchange(exchange).setup(token)
self.token_to_exchange[token] = exchange
self.exchange_to_token[exchange] = token
token_id: uint256 = self.tokenCount + 1
self.tokenCount = token_id
self.id_to_token[token_id] = token
log.NewExchange(token, exchange)
return exchange
Solidity
- 兑换池和
Token绑定, 池子和Token双向映射 - 相同的代币只能创建一个池子
- 采用
new关键字create新的池子合约
contract Factory {
mapping(address => address) tokenToExchange;
mapping(address => address) exchange_to_token;
function createExchange(address _token) public returns (address) {
require(_token != address(0), "Invalid token address");
require(
tokenToExchange[_token] == address(0),
"Exchange already registered."
);
Exchange exchange = new Exchange(_token);
tokenToExchange[_token] = address(exchange);
exchange_to_token[address(exchange)] = _token;
return address(exchange);
}
function getExchange(address _token) public view returns (address) {
return tokenToExchange[_token];
}
function getToken(address exchange) public view returns (address) {
return exchange_to_token[exchange];
}
}
Uniswap V1
背景介绍
UniswapV1 pool只允许创建Token/ETH交易对- 流动性代币实际就是
ERC20代币,支持转账 - 交易池支持直接的
Token/ETH计算兑换 Token/Token之间的兑换需要不同的交易池参与,以ETH为锚点执行兑换
- 流动性代币实际就是
Exchange
任何人通过提供 ETH/ERC20 代币提供流动性,流动性代币在提供流动性时 mint,在退款时 burn
增加流动性
- public: [addLiquidity(min_liquidity: uint256, max_tokens: uint256, deadline: timestamp)]
- 初次添加流动性:
ETH/Token直接作为交易对存储在池子ETH余额就是当前池子的流动性代币数量
- 非初次添加流动性:
- 以用户提供的
ETH为锚点,计算应该提供的相匹配的Token数量和mint出来的流动性代币数量 - 用户自定义的滑点控制交易,确保
Token数量不会超限 - 确保最终流动性代币的数量不会过低
- 以用户提供的
@public
@payable
def addLiquidity(min_liquidity: uint256, max_tokens: uint256, deadline: timestamp) -> uint256:
assert deadline > block.timestamp and (max_tokens > 0 and msg.value > 0)
total_liquidity: uint256 = self.totalSupply
if total_liquidity > 0:
// 允许用户自定义滑点,确保最终获得的流动性在滑点范围内
assert min_liquidity > 0
// 当前池子交易对中的ETH数量
eth_reserve: uint256(wei) = self.balance - msg.value
// 当前池子交易对中的Token数量
token_reserve: uint256 = self.token.balanceOf(self)
// 按照当前交易提供的 ETH 数量 和池子余额来计算应该添加的Token数量,数值向上取整
// 要求匹配的Token 数量小于用户自定义的Token最大值
token_amount: uint256 = msg.value * token_reserve / eth_reserve + 1
// 按照当前交易提供的 ETH数量 和目前池子中的流动性代币数量来计算最终获得的流动性,数值向下取整
// 要求最终流动性的值大于用户期望的最小值
liquidity_minted: uint256 = msg.value * total_liquidity / eth_reserve
assert max_tokens >= token_amount and liquidity_minted >= min_liquidity
// mint 流动性代币
self.balances[msg.sender] += liquidity_minted
self.totalSupply = total_liquidity + liquidity_minted
// 将Token代币添加到流动池
assert self.token.transferFrom(msg.sender, self, token_amount)
// 抛出事件
log.AddLiquidity(msg.sender, msg.value, token_amount)
log.Transfer(ZERO_ADDRESS, msg.sender, liquidity_minted)
return liquidity_minted
else:
// 初次添加流动性
// 判断当前工厂合约、Token合约的合法性
// 初次添加流动性,要求最少的ETH数量为 1 GWEI
assert (self.factory != ZERO_ADDRESS and self.token != ZERO_ADDRESS) and msg.value >= 1000000000
// 判断交易池的合约地址,只能添加当前池子Token代币
assert self.factory.getExchange(self.token) == self
// 初次添加流动性时,将全部代币转入流动性池
token_amount: uint256 = max_tokens
// 初次添加流动性时,将ETH转账额作为Token的初始交易对。
// ETH 初次额度就是当前交易池的流动性
initial_liquidity: uint256 = as_unitless_number(self.balance)
self.totalSupply = initial_liquidity
// 将流动性代币 mint 到交易发送地址
self.balances[msg.sender] = initial_liquidity
// 将Token代币添加到交易池
assert self.token.transferFrom(msg.sender, self, token_amount)
// 抛出事件
log.AddLiquidity(msg.sender, msg.value, token_amount)
log.Transfer(ZERO_ADDRESS, msg.sender, initial_liquidity)
return initial_liquidity
移除流动性
- public: [removeLiquidity(amount: uint256, min_eth: uint256(wei), min_tokens: uint256, deadline: timestamp)]
- 移除流动性
- 以用户提供的流动性代币数量为锚点,计算应该退还的
ETH和Token数量 - 用户自定义滑点,确保退换的
ETH 和 Token满足用户期望
- 以用户提供的流动性代币数量为锚点,计算应该退还的
@public
def removeLiquidity(amount: uint256, min_eth: uint256(wei), min_tokens: uint256, deadline: timestamp) -> (uint256(wei), uint256):
assert (amount > 0 and deadline > block.timestamp) and (min_eth > 0 and min_tokens > 0)
total_liquidity: uint256 = self.totalSupply
assert total_liquidity > 0
// 交易池中Token的总数量
token_reserve: uint256 = self.token.balanceOf(self)
// 根据移除的流动性代币数量占据总流动性的比例,计算池子中应该退回的ETH数量
eth_amount: uint256(wei) = amount * self.balance / total_liquidity
// 根据移除的流动性代币数量占据总流动性的比例,计算池子中应该退回的Token数量
token_amount: uint256 = amount * token_reserve / total_liquidity
//根据用户自定义的滑点,确保退换的ETH 和 Token在可接受的范围内
assert eth_amount >= min_eth and token_amount >= min_tokens
// 去除流动性
self.balances[msg.sender] -= amount
self.totalSupply = total_liquidity - amount
// 退还 ETH
send(msg.sender, eth_amount)
// 退还Token代币
assert self.token.transfer(msg.sender, token_amount)
// 抛出事件
log.RemoveLiquidity(msg.sender, eth_amount, token_amount)
log.Transfer(msg.sender, ZERO_ADDRESS, amount)
return eth_amount, token_amount
根据交易池输入计算输出
$$\Delta y = \frac{y r \Delta x}{x + r \Delta x}$$
UniswapV1 交易会抽取0.3%的手续费,作为提供流动性的奖励(计算恒定乘积的时候扣除手续费,但是交易池整体的余额增加,导致整体的乘积上涨,每笔交易都会让恒定乘积上涨。)
private: [getInputPrice(input_amount: uint256, input_reserve: uint256, output_reserve: uint256)]
@private
@constant
def getInputPrice(input_amount: uint256, input_reserve: uint256, output_reserve: uint256) -> uint256:
assert input_reserve > 0 and output_reserve > 0
// 输入的资产需要扣除一部分手续费
input_amount_with_fee: uint256 = input_amount * 997
numerator: uint256 = input_amount_with_fee * output_reserve
denominator: uint256 = (input_reserve * 1000) + input_amount_with_fee
return numerator / denominator
根据交易池输出反推输入
$$\Delta x = \frac{x \Delta y}{r(y - \Delta y)}$$
private: [getOutputPrice(output_amount: uint256, input_reserve: uint256, output_reserve: uint256)]
@private
@constant
def getOutputPrice(output_amount: uint256, input_reserve: uint256, output_reserve: uint256) -> uint256:
assert input_reserve > 0 and output_reserve > 0
numerator: uint256 = input_reserve * output_amount * 1000
denominator: uint256 = (output_reserve - output_amount) * 997
return numerator / denominator + 1
多个交易池兑换Token
用户进行 Token-Token 的 Swap,根据不同交易池的 ETH 锚定数量
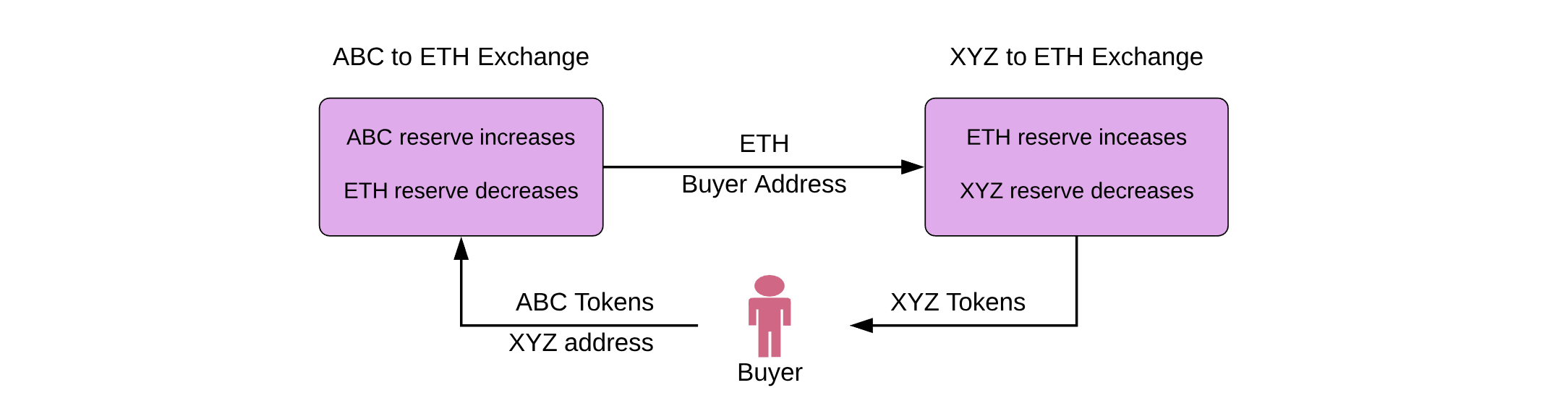
@public
def tokenToEthTransferOutput(eth_bought: uint256(wei), max_tokens: uint256, deadline: timestamp, recipient: address) -> uint256:
assert recipient != self and recipient != ZERO_ADDRESS
return self.tokenToEthOutput(eth_bought, max_tokens, deadline, msg.sender, recipient)
@private
def tokenToTokenInput(tokens_sold: uint256, min_tokens_bought: uint256, min_eth_bought: uint256(wei), deadline: timestamp, buyer: address, recipient: address, exchange_addr: address) -> uint256:
assert (deadline >= block.timestamp and tokens_sold > 0) and (min_tokens_bought > 0 and min_eth_bought > 0)
assert exchange_addr != self and exchange_addr != ZERO_ADDRESS
token_reserve: uint256 = self.token.balanceOf(self)
// 通过输入计算预期输出
// 卖出TokenA,计算预期的ETH数量
eth_bought: uint256 = self.getInputPrice(tokens_sold, token_reserve, as_unitless_number(self.balance))
wei_bought: uint256(wei) = as_wei_value(eth_bought, 'wei')
assert wei_bought >= min_eth_bought
assert self.token.transferFrom(buyer, self, tokens_sold)
// 根据卖出的ETH,购入TokenB
tokens_bought: uint256 = Exchange(exchange_addr).ethToTokenTransferInput(min_tokens_bought, deadline, recipient, value=wei_bought)
log.EthPurchase(buyer, tokens_sold, wei_bought)
return tokens_bought
Reference
https://hackmd.io/C-DvwDSfSxuh-Gd4WKE_ig
https://github.com/Uniswap/v1-contracts/blob/master/contracts/uniswap_exchange.vy
UniswapV1 In Solidity
Factory工厂合约
pragma solidity ^0.8.0;
contract Factory {
mapping(address => address) tokenToExchange;
mapping(address => address) exchange_to_token;
function createExchange(address _token) public returns (address) {
require(_token != address(0), "Invalid token address");
require(
tokenToExchange[_token] == address(0),
"Exchange already registered."
);
Exchange exchange = new Exchange(_token);
tokenToExchange[_token] = address(exchange);
exchange_to_token[address(exchange)] = _token;
return address(exchange);
}
function getExchange(address _token) public view returns (address) {
return tokenToExchange[_token];
}
function getToken(address exchange) public view returns (address) {
return exchange_to_token[exchange];
}
}
Exchange
pragma solidity ^0.8.0;
import "@openzeppelin/contracts/token/ERC20/IERC20.sol";
import "@openzeppelin/contracts/token/ERC20/ERC20.sol";
interface IExchange {
function ethToTokenSwap(uint256 _minTokens, address recipient)
external
payable;
function ethToTokenTransfer(uint256 _minTokens, address _recipient)
external
payable;
}
interface IFactory {
function getExchange(address _tokenAddress) external returns (address);
function getToken(address exchange) external returns (address);
}
contract Exchange is ERC20 {
address public tokenAddress;
address public factoryAddress;
constructor(address _token) ERC20("Uniswap-V1", "UNI1") {
require(_token != address(0), "invalid token address");
tokenAddress = _token;
factoryAddress = msg.sender;
}
function addLiquidity(
uint256 min_liquidity,
uint256 max_tokens,
uint256 deadline
) public payable {
require(deadline > block.timestamp);
require(msg.value > 0 && max_tokens > 0);
uint256 total_liquidity = totalSupply();
IERC20 token = IERC20(tokenAddress);
if (total_liquidity == 0) {
require(
factoryAddress != address(0) &&
tokenAddress != address(0) &&
msg.value > 1 gwei
);
address exceptedExchange = IFactory(factoryAddress).getExchange(
tokenAddress
);
require(exceptedExchange == address(this));
token.transferFrom(msg.sender, address(this), max_tokens);
uint256 liquidity = address(this).balance;
_mint(msg.sender, liquidity);
} else {
require(min_liquidity > 0);
uint256 ethReserve = address(this).balance - msg.value;
uint256 tokenReserve = getReserve();
uint256 _minTokenAmount = (msg.value * tokenReserve) /
ethReserve +
1; //向上取整
uint256 liquidity = (totalSupply() * msg.value) / ethReserve;
require(
max_tokens >= _minTokenAmount && liquidity >= min_liquidity,
"Insufficient token for liquidity"
);
token.transferFrom(msg.sender, address(this), _minTokenAmount);
_mint(msg.sender, liquidity);
}
}
function removeLiquidity(
uint256 amount,
uint256 min_eth,
uint256 min_tokens,
uint256 deadline
) public returns (uint256, uint256) {
require(amount > 0, "Invalid amount");
require(deadline > block.timestamp);
uint256 ethAmount = (amount * address(this).balance) / totalSupply();
uint256 tokenAmount = (amount * getReserve()) / totalSupply();
require(ethAmount >= min_eth && tokenAmount >= min_tokens);
_burn(msg.sender, amount);
IERC20(tokenAddress).transfer(msg.sender, tokenAmount);
payable(msg.sender).transfer(ethAmount);
return (ethAmount, tokenAmount);
}
function getReserve() public view returns (uint256) {
return IERC20(tokenAddress).balanceOf(address(this));
}
// Swap fee: 3%
// 通过存入的资产计算能够兑换到的资产数量
function getInputPrice(
uint256 input_amount,
uint256 inReserve,
uint256 outReserve
) public pure returns (uint256) {
require(inReserve > 0 && outReserve > 0);
uint256 inputAmountWithFee = input_amount * 997;
uint256 numerator = outReserve * inputAmountWithFee;
uint256 denominator = inReserve * 1000 + inputAmountWithFee;
return numerator / denominator;
}
// 通过卖出资产计算能够兑换到的资产数量
function getOutputPrice(
uint256 output_amount,
uint256 inReserve,
uint256 outReserve
) public pure returns (uint256) {
require(inReserve > 0 && outReserve > 0);
uint256 numerator = inReserve * output_amount * 1000;
uint256 denominator = 997 * (outReserve - output_amount);
return numerator / denominator + 1;
}
function getTokenAmount(uint256 _ethSold) public view returns (uint256) {
require(_ethSold > 0, "Invalid Amount");
return getInputPrice(_ethSold, address(this).balance, getReserve());
}
function getEthAmount(uint256 _tokenSold) public view returns (uint256) {
require(_tokenSold > 0, "Invalid Amount");
return getInputPrice(_tokenSold, getReserve(), address(this).balance);
}
function ethToTokenSwap(uint256 _minToken, address recipient)
public
payable
{
uint256 tokenAmount = getInputPrice(
msg.value,
address(this).balance - msg.value,
getReserve()
);
require(tokenAmount >= _minToken, "Insufficient token amount");
IERC20 token = IERC20(tokenAddress);
token.transfer(recipient, tokenAmount);
}
function tokenToEthSwap(uint256 _minEth, uint256 _tokenSold) public {
uint256 ethAmount = getEthAmount(_tokenSold);
require(ethAmount >= _minEth, "Insufficient eth amount");
IERC20(tokenAddress).transferFrom(
msg.sender,
address(this),
_tokenSold
);
payable(msg.sender).transfer(ethAmount);
}
function tokenToTokenSwap(
uint256 tokens_sold,
uint256 min_tokens_bought,
uint256 min_eth_bought,
uint256 _minBoughtTokenAmount,
address _anotherToken,
address recipient
) public {
address exchangeAddress = IFactory(factoryAddress).getExchange(
_anotherToken
);
require(exchangeAddress != address(0), "This token has no exchange.");
uint256 tokenReserve = getReserve();
uint256 ethBought = getInputPrice(
tokens_sold,
tokenReserve,
address(this).balance
);
require(ethBought >= min_eth_bought);
IERC20(tokenAddress).transferFrom(
msg.sender,
address(this),
tokens_sold
);
IExchange(exchangeAddress).ethToTokenSwap{value: ethBought}(
_minBoughtTokenAmount,
recipient
);
}
}
Tokens
pragma solidity ^0.8.0;
contract Token is ERC20 {
constructor(
string memory name,
string memory symbol,
uint256 initialSupply
) ERC20(name, symbol) {
_mint(msg.sender, initialSupply);
}
}
UniswapV2 架构
Uniswap 是一款 DeFi 应用,允许交易者以无需信任的方式将一种代币兑换成另一种代币。
它是早期的自动交易做市商之一。
自动化做市商是订单簿的替代品,我们假设读者已经熟悉它。
恒定函数做市商 (Constant Function Market Makers)
一个自动做市商在池子(智能合约)中持有两种代币(代币 X 和代币 Y)。
它允许任何人从池子中取出代币 X,但必须存入一定数量的代币 Y,以使池子中的资产“总额”不会减少,我们认为“总额”是两种资产金额的乘积
同时使用代币兑换另一种代币,需要付出一定手续费,因此 (x + r $\Delta x$)(y - $\Delta y$) = xy
xy <= x’y’ ,其中 xy表示兑换前的代币数量乘积,x’y’表示兑换完成后的代币数量乘积
这保证了资产池的资产持有量只能保持不变或增加。大多数资产池都会收取某种费用。余额的乘积不仅应该增加,而且应该至少增加一定数额以抵消费用。
资产由流动性提供者提供给资金池,流动性提供者会收到所谓的 LP 代币来代表其在资金池中的份额。流动性提供者余额的跟踪方式与ERC 4626 的工作方式类似。
- 自动做市商
AMM和ERC4626之间的区别在于,ERC4626仅支持一种资产,而AMM有两种代币
AMM 优势
价格预言机
AMM 基于公式 x * y = k 运行交易池,通过内部代币的数量决定兑换价格
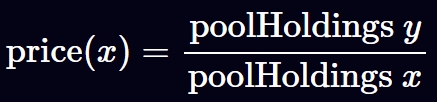
价格总是跟内部代币的数量相关,当单一交易池的代币价格脱锚后,其它 DEX 可以通过套利平衡每个交易池的价格
DEX 的代币价格总是和池子中的代币数量相关,因此可以作为链上代币价格的语言机。
但是,DEX 的价格容易受到链上交易的影响,flash_loan 的大量代币的涌入/涌出 会造成代币瞬时的巨额波动,因此使用 AMM 去中心化交易池子作为价格 oracle 需要谨慎考虑价格的波动性
比订单薄更节省gas
订单簿需要大量的记账工作。AMM 只需要持有两个代币并按照简单的规则进行转移,这使得它们实施起来更有效率。
AMM 劣势
自动化做市商有两个主要缺点:1)价格总是变动;2)流动性提供者的无常损失。
价格波动
即使是小额订单也会影响 AMM 中的价格
如果您下单购买 100 股 Apple 股票,您的订单不会导致价格变动,因为有数千股股票可以按照您指定的价格出售。自动做市商则不会出现这种情况。每笔交易,无论多小,都会影响价格。
AMM DEX 中任意交易都会引起兑换价格的波动,买入或卖出订单通常会比订单簿模型遇到更多的滑点,而交换机制会引发三明治攻击。
MEV
在 AMM 中,三明治攻击基本上是不可避免的
由于每笔订单都会影响价格,MEV(最大可提取价值)交易者会等待足够大的买单,然后在受害者的订单之前下达买单,并在受害者的订单之后下达卖单。领先的买单会推高原始交易者的价格,从而导致他们的执行情况更差。这被称为三明治攻击,因为受害者的交易被“夹”在攻击者之间。
1)攻击者的首次购买(抢先交易):为受害者推高价格
2)受害者的购买:进一步推高价格
3)攻击者的卖出:卖出首次购买的股票并获利
无常损失
无常损失表示在池子币价下跌时造成的损失,因为在 AMM 等去中心化的交易所中,流动性提供者自动成为代币对的买方和卖方,一旦有人发起交易,就会改变池子币价。
无常损失的公式为:
(Value_pool - Value_hold)/Value_hold * 100%
比如,在1ETH=10U的背景下,ETH 涨到 1 ETH = 1000U 时的无常损失为:
- 正常持有:
- 原本价值(
1ETH+10U = 10U+10U = 20U) - ETH上涨后的价值(
1ETH+10U = 1000U+10U = 1010U) - 利润为(
1010U-20u=990U)
- 原本价值(
- 用户创建
DEXDEX中一共有 (1ETH,10U) 的代币对,此时ETH/U的价格为1ETH=10U- 由于不停有人购入
ETH,最终ETH上涨至1000U,此时池子剩余 (0.1ETH,100U) - 上涨后,
DEX创建者的剩余代币的价值为(0.1ETH+100U = 0.1*1000U+100U = 100U + 100U = 200U) - 利润为 (
200U-20U=180U)
- 此时的无常损失率为 (
990-180/990*100% = 81.82%)
Uniswap V2 的架构
UniswapV2 的架构出奇地简单。其核心是 UniswapV2Pair 合约,该合约持有两个 ERC20 代币,交易者可以互换,或者流动性提供者可以为其提供流动性。
如果所需的 UniswapV2Pair 合约不存在,则可以从 UniswapV2Factory 合约中无需许可地创建一个新的合约。
UniswapV2Pair 合约也是 ERC20 代币,代币表示流动性份额,类似于 ERC4626 的工作方式。
虽然高级交易者或智能合约可以直接与货币对合约进行交互,但大多数用户还是会通过路由器合约与货币对进行交互,路由器合约具有多种便利功能,例如可以在一次交易中在货币对之间进行交易,如果货币对不存在,则创建一个“合成”货币对。
工厂合约,用于创建池子:https://github.com/Uniswap/v2-core/blob/master/contracts/UniswapV2Factory.sol
Pair 交易池合约: https://github.com/Uniswap/v2-core/blob/master/contracts/UniswapV2Pair.sol
Route: https://github.com/Uniswap/v2-periphery/tree/master/contracts
找到交易对
智能合约不是访问从代币对到池地址的映射,而是通过预测 create2 地址作为代币地址和工厂地址的函数来计算池的地址。
由于没有存储访问,因此这非常节省 gas。下面是 UniswapV2Library 提供的用于计算 Pair 合约地址的辅助函数。
function pairFor(
address factory,
address tokenA,
address tokenB
) public pure returns (address pair) {
require(tokenA != tokenB, "UniswapV2: IDENTICAL_ADDRESSES");
(address token0, address token1) = tokenA < tokenB
? (tokenA, tokenB)
: (tokenB, tokenA);
require(token0 != address(0), "UniswapV2: ZERO_ADDRESS");
bytes memory bytecode = getPairCodes();
pair = address(
uint256(
keccak256(
abi.encodePacked(
hex"ff",
factory,
keccak256(abi.encodePacked(token0, token1)),
keccak256(bytecode) // init code hash
)
)
)
);
}
每个交易对不使用代理模式
EIP1167 最小代理模式用于创建类似合约的集合,那么为什么不在这里使用它呢?
虽然部署成本更低,但由于 delegatecall ,每笔交易将额外增加 2,600 gas 。
由于池子旨在频繁使用,部署节省的成本最终会在几百笔交易后消失,因此值得将池子部署为新合约。
Reference
https://www.rareskills.io/uniswap-v2-book
https://www.rareskills.io/post/eip-1167-minimal-proxy-standard-with-initialization-clone-pattern
https://www.rareskills.io/post/uniswap-v2-tutorial
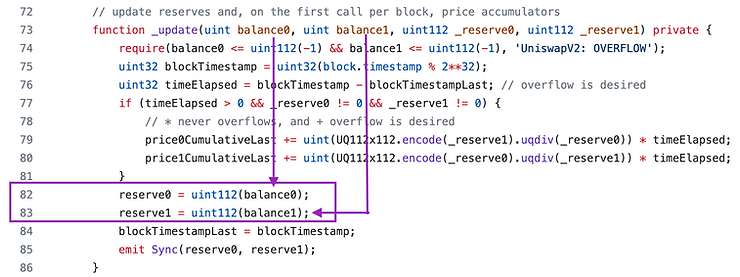
Swap
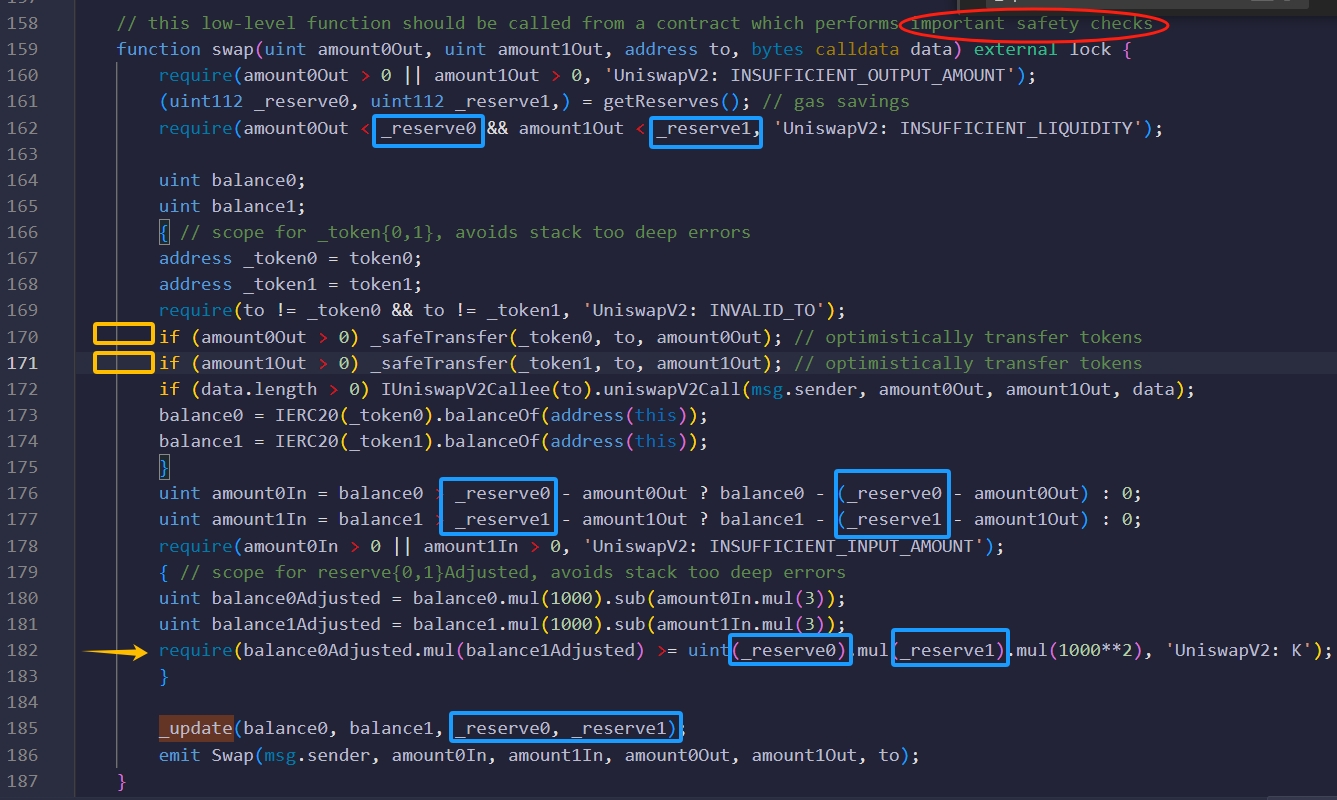
- 在第
170-171行(用黄色框表示),该函数直接转出交易者在函数参数中请求的代币数量。- 函数内部没有转入代币的地方。
swap代码中不存在代币转入的地方,但这并不意味着我们可以直接调用swap并提取我们想要的所有代币!
- 我们之所以可以立即移除代币,是为了可以进行闪电贷。
- 当然,第
182行的require语句(橙色箭头)将要求我们连本带利地偿还闪电贷。
- 当然,第
- 在该函数的顶部,有一条注释,指出该函数应从另一个实施重要安全检查的智能合约调用。
- 这意味着该函数缺少安全检查(红色下划线)
- 变量 _
reserve0和 _reserve1(蓝色下划线)在第161行、第176-177行、第182行被读取,但是在本函数中没有被写入。 - 第
182行(橙色箭头)并不严格检查X × Y = K。它检查balance1Adjusted × balance2Adjusted ≥ K。- 这是唯一执行“有趣”操作的
require语句。 - 其他
require语句检查值是否不为零,或者您是否没有将代币发送到它们自己的合约地址。
- 这是唯一执行“有趣”操作的
balance0和balance1直接使用ERC20 balanceOf从pair合约的实际余额中读取- 第
172行(黄色框下方)仅当数据非空时才执行,否则不执行
利用这些观察结果,我们将逐一理解该函数的一个特征。
闪电借贷
用户不必使用兑换功能来交易代币,它可以纯粹用作闪电贷。

借款合约只需请求他们希望借入的代币数量(A),无需抵押,然后它们将被转移到合约(B)。
函数调用时需要提供的数据作为函数参数(C)传入,然后传递给实现 IUniswapV2Callee。
uniswapV2Call 函数必须偿还闪电贷和费用,否则交易将被撤销。
交换需要使用智能合约
Uniswap V2 “衡量”发送的代币数量的方式在第 176 行和 177 行完成,如下方黄色框标记。
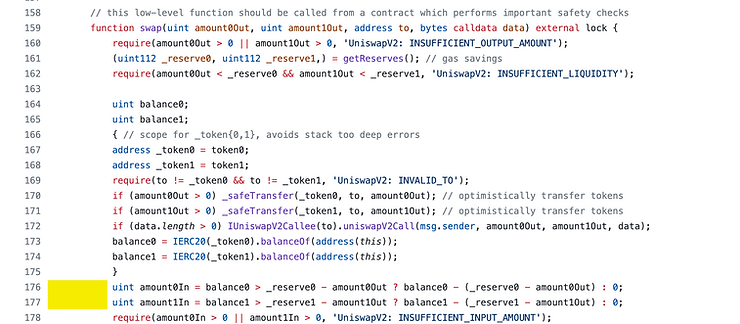
请记住,_reserve0 和 _reserve1 不会在此函数内更新。它们反映的是作为交换的一部分发送新代币集之前的合约余额。
对于该对中的两个标记,可能会发生以下两种情况之一:
- 该池中某种代币的数量净增加。
- 该池中某种代币的数量净减少(或没有变化)。
代码通过以下逻辑确定发生了哪种情况:
currentContractbalanceX > _reserveX - _amountXOut
// alternatively
currentContractBalanceX > previousContractBalanceX - _amountXOut
如果测量到净减少量,三元运算符将返回零,否则它将测量代币的净收益。
amountXIn = balanceX - (_reserveX - amountXOut)
// alternatively
amountXIn = currentContractBalanceX - (previousContractBalanceX - amountXOut)
由于第 162 行的 require 语句,所以情况总是 _reserveX > amountXOut。
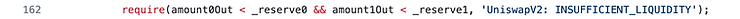
一些例子。
- 假设我们之前的余额是
10,amountOut = 0,currentBalance = 12。- 满足:
currentContractBalanceX > previousContractBalanceX - _amountXOut => 12 > 10-0 amountXIn = 12 -(10-0) = 2,用户存入了2个代币。
- 满足:
- 假设我们之前的余额为
10,amountOut = 7,currentBalance = 3。- 不满足:
currentContractBalanceX > previousContractBalanceX - _amountXOut => 3 > 10-7 - 这意味着
amountXIn = 0,用户存入了0个代币。
- 不满足:
- 假设我们之前的余额是
10,amountOut = 7,currentBalance =2。- 不满足:
currentContractBalanceX > previousContractBalanceX - _amountXOut => 2 > 10-7 - 这意味着
amountXIn = 0,用户存入了0个代币。
- 不满足:
- 假设我们之前的余额是
10,amountOut = 6,currentBalance = 18- 满足:
currentContractBalanceX > previousContractBalanceX - _amountXOut => 18 > 10-6 - 这意味着
amountXIn = 18-(10-6) = 14,用户存入了14个代币。 - 那么用户“借”了
6个代币,但偿还了14个代币。
- 满足:
结论:如果代币有净收益,则 amount0In 和 amount1In 将反映净收益,
如果代币有净亏损,则 amount0In 和 amount1In 将为零。
平衡 XY = K
现在我们知道用户发送了多少个 Token,让我们看看如何强制 XY >= K

Uniswap V2 每次交换收取 0.3% 的硬编码费用,这就是我们看到数字 1000 和 3 的原因
费用会计
但我们不仅希望 K 变得更大,还希望它至少增大到强制执行 0.3% 费用的量。
具体来说,0.3% 的费用适用于我们的交易规模,而不是资金池的规模。
它仅适用于流入的代币,而不适用于流出的代币。以下是一些示例:
假设我们放入 1000 个 token0,取出 1000 个 token1,我们需要为 token0 支付 3 的费用,而为 token1 则无需支付费用。
假设我们借了 1000 个 token0,但没有借 token1。我们将不得不再投入 1000 个 token0,并且需要为此支付 0.3% 的费用——3 个 token0。
请注意,如果我们快速借入其中一种代币,其费用与以相同金额交换该代币的费用相同。您需要为存入的代币支付费用,而不是为取出的代币支付费用。但如果您不存入代币,则无法借入或交换。

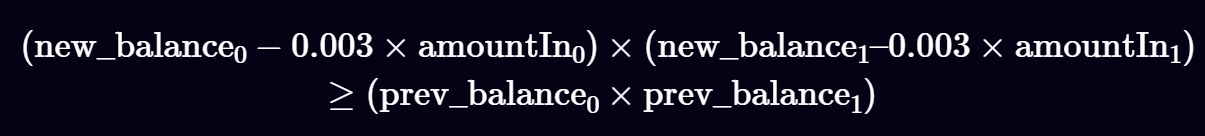
也就是说,新的余额必须增加 0.3%。在代码中,公式通过将每个项乘以 1,000 来缩放,因为 Solidity 没有浮点数,但数学公式显示了代码试图完成的任务。
更新储备
现在交易已完成,那么“先前余额”必须替换为当前余额。这发生在 swap() 末尾对 _update() 函数的调用中。
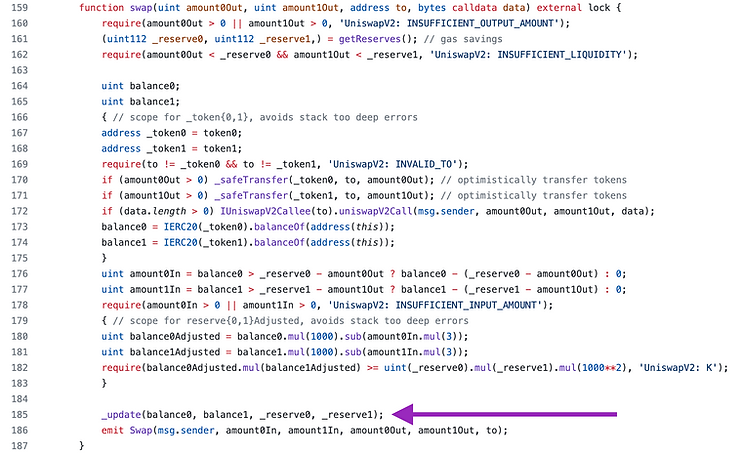
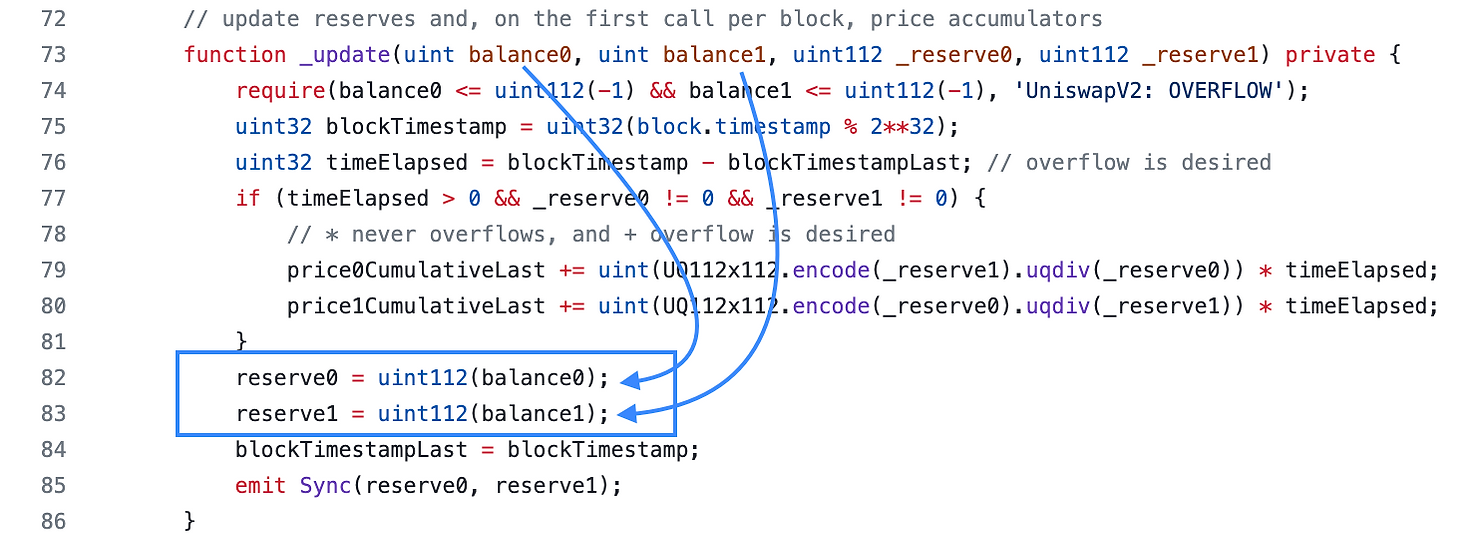
_update() 函数
这里有很多逻辑来处理 TWAP 预言机,但我们现在只关心第 82 行和第 83 行,其中存储变量 reserve0 和 reserve1 被更新以反映更改后的余额。参数 _reserve0 和 _reserve1 用于更新预言机,但它们不会被存储。
安全检查
有两件事可能会出错:
amountIn 不是强制最优的,因此用户可能会为交换支付过多的费用
AmountOut 不具备灵活性,因为它是作为参数提供的。如果 amountIn 相对于 amountOut 不够,交易将撤销,gas 将被浪费。
如果有人抢先交易(有意或无意),并将池中的资产比例改变到不利的方向,就会发生这些情况。
Reference
https://www.rareskills.io/post/uniswap-v2-swap-function
流动性
Uniswap V2 铸币和销毁功能详解
UniswapV2 的生命周期是从第一次添加流动性铸造 LP 代币(提供流动性,即向池中提供代币)开始,然后其他人添加流动性,进行交换,然后最终流动性提供者烧毁他们的 LP 代币来赎回池代币。
事实证明,反向研究这些功能更容易——销毁、铸造流动性、然后铸造初始流动性。
那么我们就从 Burn 开始吧。
Uniswap V2 销毁
在销毁流动性代币之前,池中需要有流动性,所以我们做出这样的假设。我们假设系统中有两种代币:token0,token1。
我们在下面注释了刻录功能,我们将解释那些不太明显的部分
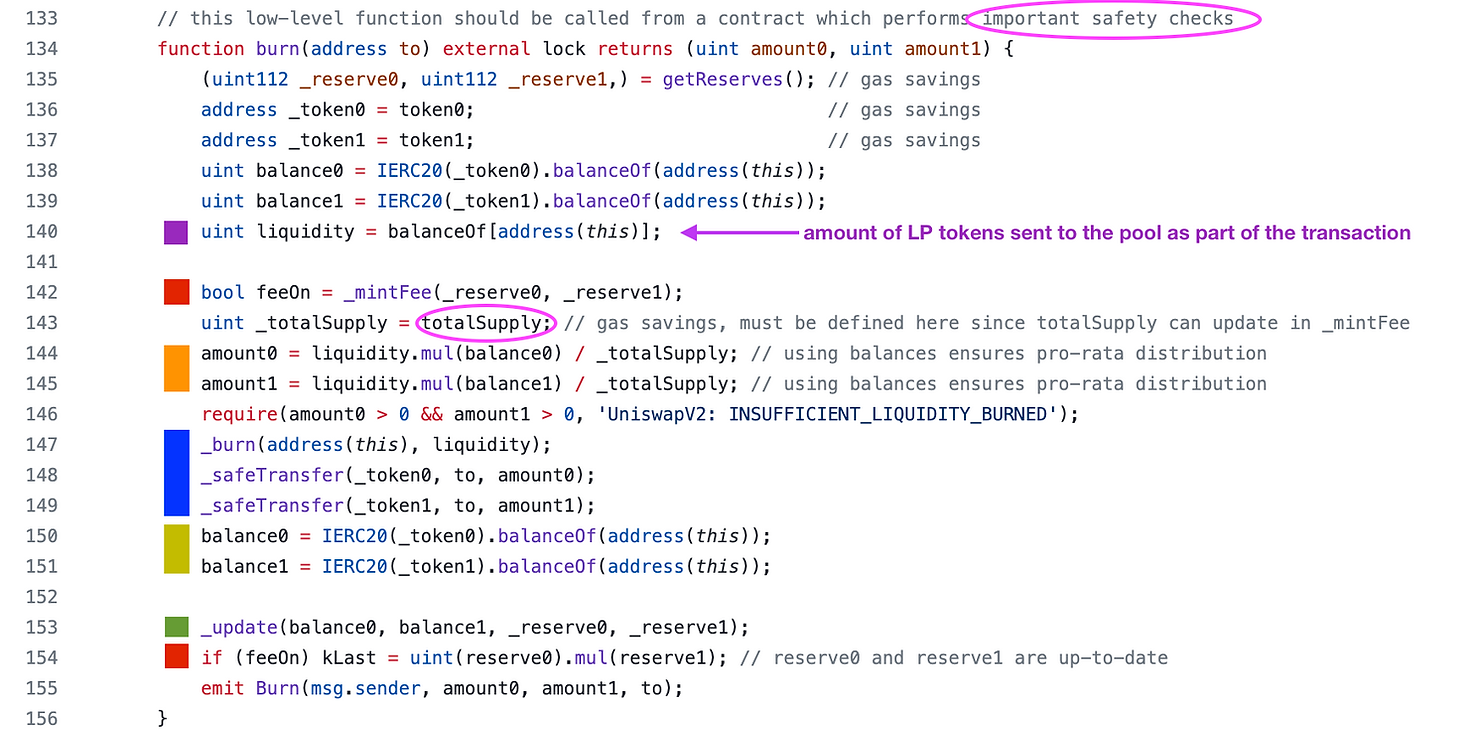
- 在第
140行(紫色框)中,流动性由池合约拥有的LP代币数量来衡量。- 假设销毁者在调用销毁之前发送了
LP代币,但建议将其作为一笔交易的一部分。 - 如果将它们作为两笔交易发送,其他人可能会销毁您的 LP 代币并消除您的流动性!
- 用户发送给合约的
LP将被销毁。 - 一般来说,我们可以假设平时,合约的
LP代币余额为零,因为如果LP代币只是放在配对合约中,有人会销毁它们并免费索取其中的一部分token0
- 假设销毁者在调用销毁之前发送了
- 第
144行至第145行的橙色框是计算LP提供者将收回的金额的地方。Liquidity / totalSupply是他们在 LP 代币总供应量中所占的销毁份额。- 基于
Burn的LP份额,计算应该赎回的(token0,token1)的数量 - 如果流动性代币的总供应量为
1,000,而他们销毁了100 个 LP代币,那么他们将占据(100/1000 = 10%)的 LP 代币
147到149行的蓝色框是LP代币实际被烧毁的地方,并把(token0,token1)发送给给流动性燃烧者。150-151行的黄色框计算新的余额变量,因此_update()的调用可以更新_reserve变量。除了更新TWAP之外,该_update函数还只是更新_reserve变量
安全检查
假设池中有等量的 token0 和 token1。
这意味着销毁者在销毁 LP 代币时希望收到等量的代币。
但是,销毁交易签署交易和确认之间,池中 token 的数量可能会发生变化,uniswapV2 使用 BalanceOf 查询每种代币的在池中的余额。
如果销毁者的确认逻辑依赖于接收特定数量),那么如果收到的或略少于预期数量的话,该逻辑可能会崩溃。
销毁 LP 时,合约必须准备好接收少于或低于预期的金额
当资金池不空时创造流动性
这是 mint 流动性函数。
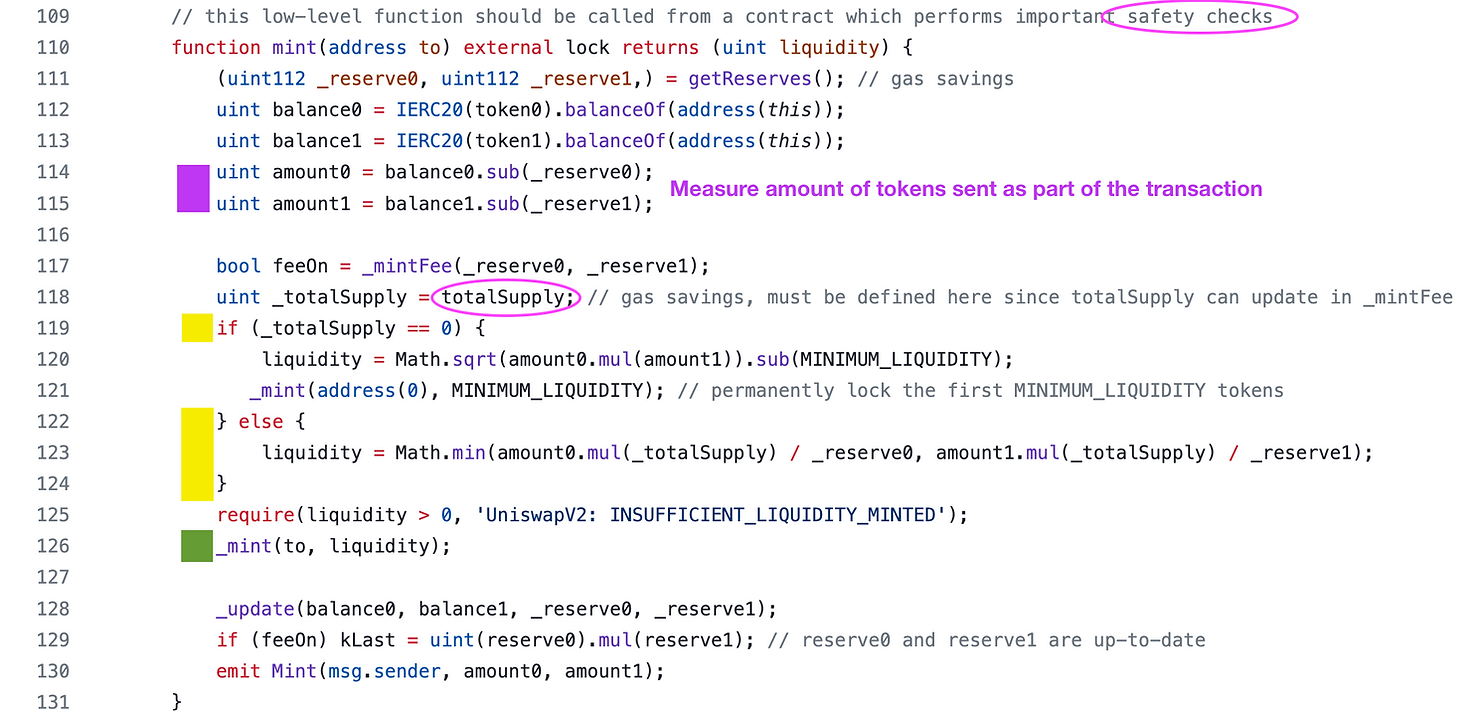
如果池子非空的,即流动性代币的总供应量大于零,在第 126 行(绿色框)中铸造给他们的流动性是两个值中较小的一个。
liquidity = Math.min(amount0.mul(_totalSupply) / _reserve0, amount1.mul(_totalSupply) / _reserve1);
这行代码测量的比例是 amount0 / _reserve0 ——按 totalSupplyLP 代币的比例缩放。
假设池子中有 10token0 和 10 token1。
如果用户提供 10token0 和 0 token1,他们将获得最小值 (10/10, 0/10) 并获得零流动性代币!
如果我们取两个比率中的最大值?
假设池中目前有 100 个token0 和 1 个 token1,LP 代币的供应量为 1。假设两种代币的总价值(以美元计)为 200
那么有人可以再提供一个 Token1 ,按照最大值将会 mint Max(0/10,1/1) = 1 个 LP 代币
此时,池子的总流动性代币是 1 + 1 = 2,用户的流动性代币是 1,池子的总价值为 300
这意味着用户拥有 50% 的 LP 代币供应量,但是只需存入 100 美元即可。这显然是从其他 LP 提供商那里窃取的。
供给比率安全检查
用户可能会尝试遵守代币比率,但如果另一笔交易在他们之前执行并将余额更改为更大的 token0,token1 ,那么他们将获得比预期更少的流动性代币。
TotalSupply 安全检查
就像烧毁的情况一样,totalSupplyLP 代币的数量可能会随时发生变化,因此必须实施一些滑点保护。
首次添加流动性问题
与任何 LP 池一样,Uniswap V2 需要防御“通货膨胀攻击”。
Uniswap V2 的防御方法是先销毁 MINIMUM_LIQUIDITY = 10**3 的流动性代币 ,以确保没有人拥有全部 LP 代币供应并可以轻松操纵价格。
更有趣的问题是,为什么 UniswapV2 要对所供应的代币的乘积取平方根来计算要铸造的 LP 数量。
if (_totalSupply == 0) {
liquidity = Math.sqrt(amount0.mul(amount1)).sub(MINIMUM_LIQUIDITY);
_mint(address(0), MINIMUM_LIQUIDITY); // permanently lock the first MINIMUM_LIQUIDITY tokens
}
白皮书的理由如下:
Uniswap v2 initially mints shares equal to the geometric mean of the amounts, liquidity = sqrt(xy). This formula ensures that the value of a liquidity pool share at any time is essentially independent of the ratio at which liquidity was initially deposited… The above formula ensures that a liquidity pool share will never be worth less than the geometric mean of the reserves in that pool.
上述公式确保流动性池份额的价值永远不会低于该池中储备的几何平均值,这部分份额永远不会被burn,同时池子中永远都会预留一部分 (token0,token1)
获得某种直觉的最佳方法之一是插入价值观并观察会发生什么,所以让我们这样做吧。
示例:流动性翻倍
假设我们没有用平方根函数来衡量流动性:
一开始池子里有 10 个token0,10 个token1
后来,池子里有 20 个token0,20 个token1。
直观地看,流动性是翻了两倍还是翻了四倍?
因为如果我们不开平方,流动性将从 100(10×10)开始,最终达到 400(20×20)
但是,流动性并没有翻四倍。在流动性增长后,每个代币的流动性“深度”翻了一番,而不是翻了四倍。
Reference
https://www.rareskills.io/post/uniswap-v2-mint-and-burn
Uniswap 协议手续费
Uniswap V2 如何计算 mintFee
UniswapV2 的设计目标是将 1/6 的 swapFee 转入 Uniswap Protocal
由于 swapFeeRatio = 0.3%,其 1/6 = 0.05%,因此每笔 swap 交易手续费的 0.05% 将计入协议。
在交换期间收取协议费用效率低下
Uniswap 协议每笔 swap 交易收取 0.05% 的费用是低效的,因为这需要额外的代币转移。
转移 ERC20 代币需要存储更新,因此转移到协议收益地址的成本会高得多。
因此,当流动性提供者调用 burn 或 mint 时,才会计算累积的费用。 因此可以节省 gas。为了收取费用 mintFee,合约会计算自上次发生以来收取的费用金额,并向受益人地址铸造足够的 LP 代币,以使受益人有权获得 1/6 的费用。
流动性是池中代币余额乘积的平方根 liquidity = Math.sqrt(amount0.mul(amount1))
计算 mintFee 假设
为了实现这一点,Uniswap V2 依赖于以下两个不变量:
- 如果
mint()和burn()没有被调用,那么池的流动性只会增加- 多次
mint期间的swap,会增加池子的流动性。 - 每笔兑换,都会增加池子的 (token0,token1) 的代币数量
- 多次
- 流动性的增加纯粹是由于兑换手续费(或捐赠)
mintFee 计算示例
假设在
T1时,流动性池子中存在10 个 token0和10 个 token1。经过大量兑换交易,新的池余额为 40个token0 和 40个token1
此时,流动性从
10增加到40
我们希望铸造足够多的流动性代币,即 mintFee,以便协议受益人能够收到资金池全部 swapFee 的 1/6。
推导铸币费公式
在启动协议手续费的前提下,以原始流动性为起点,池子中添加了 T2-T1 时间区间的兑换手续费,我们使用以下符号:
-
s: 流动性代币基准。在T2时刻,铸造给流动性提供商的流动性代币的数量 -
$\eta$: 流动性代币基准。在
T2时刻,池子应该为协议铸造的流动性代币的数量,它应该足以赎回1/6的利润流动性 -
$\rho_{1}$: 流动性基准。在
T1时刻,池子的原始流动性Math.sqrt(_reserve0.mul(_reserve0)) -
$\rho_{2}$: 流动性基准。在
T2时刻,经过一段时间的swap手续费的积累,池子的新流动性值Math.sqrt(reserve0.mul(reserve0)) -
d: 流动性基准。 经过原始流动性和T2-T1时间区间的兑换手续费,流动性提供商获取的流动性 -
p: 流动性基准。经过T2-T1时间区间的兑换手续费, 池子应该为协议提供的流动性,它应该是时间区间内全部利润流动性的1/6
下图解答了 ,就流动性的变化而言: $\frac{s}{\eta}$ = $\frac{d}{p}$

_mintFee()Uniswap V2 的代码
考虑到这一推导,UniswapV2 _mintFee 函数的大部分内容应该是不言自明的。以下是一些符号上的变化:
T2时刻的流动性 $\rho_{2}$ 是rootKT1时刻的流动性 $\rho_{1}$ 是kLastT2时刻的流动代币数量s是totalSupply
// if fee is on, mint liquidity equivalent to 1/6th of the growth in sqrt(k)
function _mintFee(uint112 _reserve0, uint112 _reserve1) private returns (bool feeOn) {
address feeTo = IUniswapV2Factory(factory).feeTo();
feeOn = feeTo != address(0);
uint _kLast = kLast; // gas savings
if (feeOn) {
if (_kLast != 0) {
uint rootK = Math.sqrt(uint(_reserve0).mul(_reserve1));
uint rootKLast = Math.sqrt(_kLast);
if (rootK > rootKLast) {
uint numerator = totalSupply.mul(rootK.sub(rootKLast));
uint denominator = rootK.mul(5).add(rootKLast);
uint liquidity = numerator / denominator;
if (liquidity > 0) _mint(feeTo, liquidity);
}
}
} else if (_kLast != 0) {
kLast = 0;
}
}
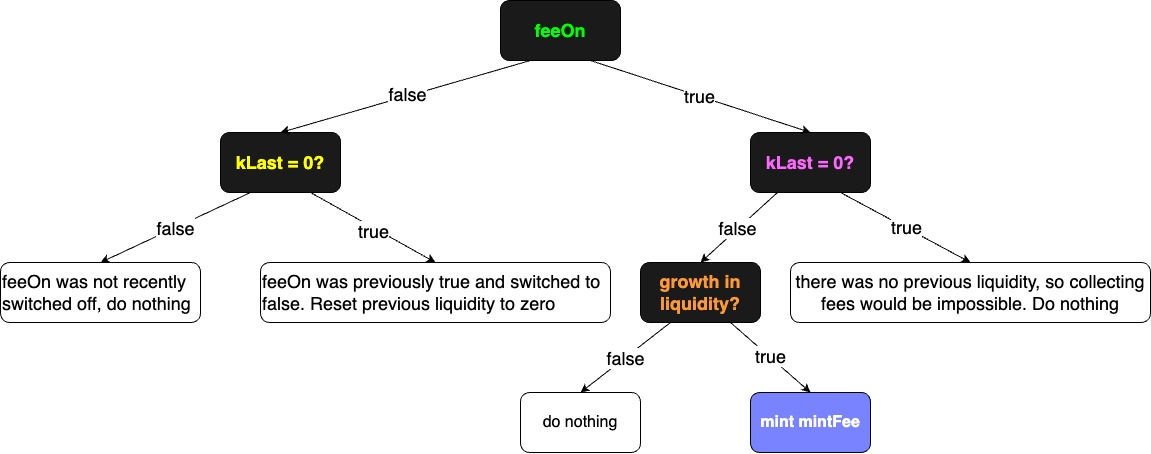
-
feeOn = false,不会为协议铸造流动性代币 -
feeOn = false,非零的kLast值置 零,不用在每次mint/burn时更新kLast的值 -
feeOn = true,但流动性没有增长,期间没有swap手续费的积累,不会为协议铸造流动性代币 -
feeOn = true, 并且存在流动性增长(期间有swap手续费的积累),因此会为协议铸造流动性代币
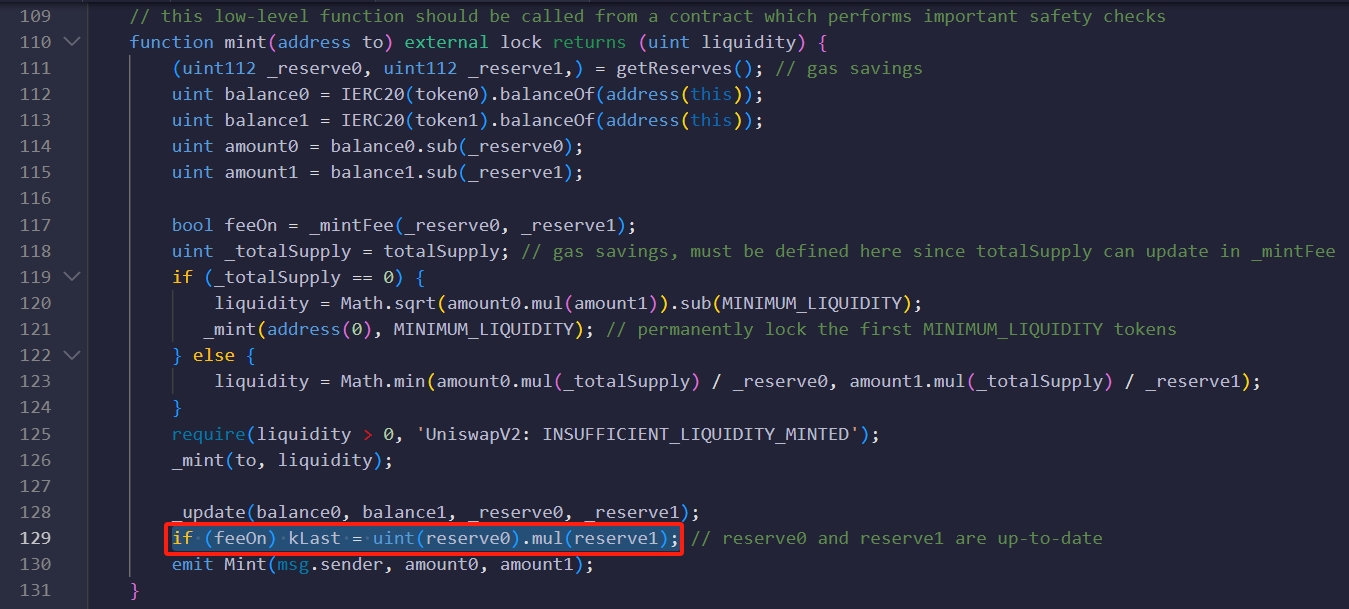
Where klast gets updated
在 mint/burn 引起的 流动性代币 totalSupply 变化的函数中,会进行 kLast 的更新。将 kLast 更新为当前行为的流动性。
Reference
https://www.rareskills.io/post/uniswap-v2-mintfee
TWAP Oracle 预言机
Uniswap 中的“价格”到底是什么?
在一个池子中(1 Ether, 2000 USDC),价格是一个比率,所以它们需要用具有小数点的数据类型来存储(Solidity 类型默认情况下没有小数点)。
也就是说,我们说以太坊是 1 Ether = 2000 USDC,而 1 USDC = 0.0005 Ether(这是忽略两种资产的小数)。
Uniswap 使用小数点两边精度为 112 位的定点数,总共占用 224 位,当与 32 位数字打包时,它会占用一个槽。
Oracle 定义
计算机科学术语中的预言机是“真相之源”, 价格预言机是价格的来源。
Uniswap 在持有两种资产时具有隐含价格,其他智能合约可以将其用作价格预言机。
预言机的目标用户是其他智能合约,因为其他智能合约可以轻松地与 Uniswap 通信以确定价格,但是仅采用余额比率来获取当前价格并不安全。
TWAP 背后的动机
测量池中资产的瞬时快照为闪电贷攻击留下了机会。也就是说,有人可以利用闪电贷进行巨额交易,导致价格暂时大幅波动,然后利用另一个使用该价格做出决策的智能合约。
Uniswap V2 预言机通过两种方式防御此问题:
- 它为价格消费者(通常是智能合约)提供了一种机制,可以取一个时间段(由用户决定)的价格平均值。这意味着攻击者必须在几个区块内不断操纵价格,这比使用闪电贷要昂贵得多。
- 它不会将当前余额纳入预言机计算中
如果池子资产流动性不强,或者取平均值的时间窗口不够大,那么资源充足的攻击者仍然可以在足够长的时间里抬高价格(或压低价格),以操纵测量时的平均价格。
TWAP 的工作原理
TWAP(时间加权平均价格)根据价格在某个水平保持的时间来计算价格权重。
- 在过去一天中,某项资产的价格在前
12小时内为10美元,在后12小时内为11美元。- 时间加权平均价格:(10 * 12 + 11 * 12) / (12 + 12) = 10.5
- 在过去一天中,资产价格在前
23小时内为10美元,在最近1个小时内为11美元。- 时间加权平均价格: (10 * 23 + 11 * 1) / (23 + 1) = 10.0417
一般来说,计算时间加权平均价格的公式为:
TWAP = $\frac{P_{1}T_{1} + P_{2}T_{2} + … + P_{n}T_{n}}{\sum_{i = 1}^{n}T_{i}}$
此处的 T 是持续时间, 表示价格在该水平保持了多长时间。
Uniswap V2 _update更新价格

Uniswap 在每次流动性发生变化时(mint/burn、swap、sync),它都会记录新的价格以及之前的价格持续了多长时间。
变量 price0Cumulativelast 和 price1CumulativeLast 是公开的,因此感兴趣的一方需要对它们进行快照。
限制时间窗口
显然,我们一般对矿池成立以来的平均价格不感兴趣。我们只想回顾一段时间(1 小时、1 天等)。
以下是 TWAP 公式。
AllTWAP = $\frac{P_{1}T_{1} + P_{2}T_{2} + P_{3}T_{3} + P_{4}T_{4} + P_{5}T_{5} + P_{6}T_{6}}{\sum_{i = 1}^{6}T_{i}} $
price0Cumulativelast = $P_{1}T_{1} + P_{2}T_{2} + P_{3}T_{3} + P_{4}T_{4} + P_{5}T_{5} + P_{6}T_{6}$
如果我们只对 T4 以来的价格感兴趣,那么我们需要执行以下操作
TWAPFromT4 = $\frac{P_{4}T_{4} + P_{5}T_{5} + P_{6}T_{6}}{\sum_{i = 4}^{6}T_{i}}$
price0CumulativelastToT3 = $P_{1}T_{1} + P_{2}T_{2} + P_{3}T_{3}$
price0CumulativelastFromT4 = price0Cumulativelast - price0CumulativelastToT3 = $P_{4}T_{4} + P_{5}T_{5} + P_{6}T_{6}$
我们在 $T_{3}$ 结束时快照价格,我们得到了值 price0CumulativelastToT3
我们在 $T_{6}$ 结束时快照价格,我们得到了值 price0Cumulativelast
price0Cumulativelast - price0CumulativelastToT3 就会得到最近窗口的累计价格。如果我们将其除以最近窗口的持续时间$T_{4} + T_{5} + T_{6}$,则得到近期窗口的 TWAP 价格。
价格累计
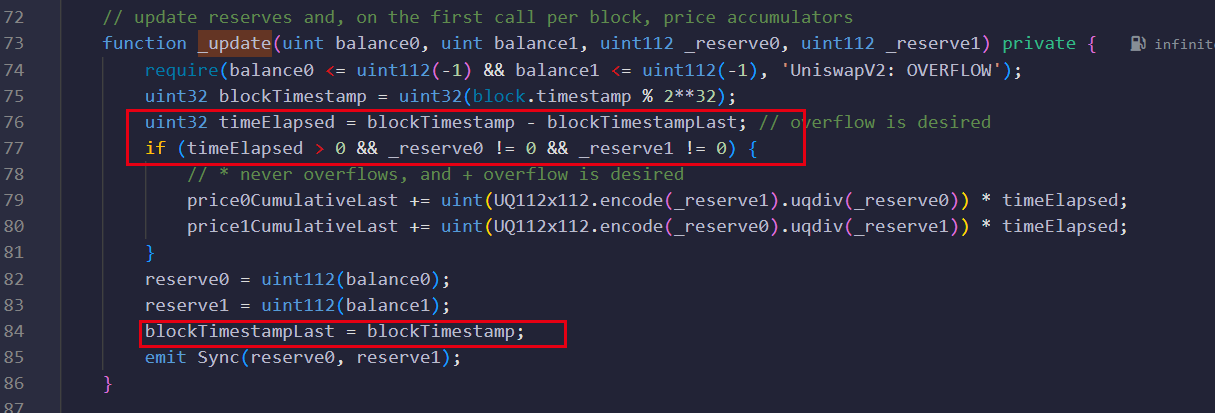
UniswapV2 只会计算并累积每个区块中涉及流动性变化的首个交易的价格,防止因为 MEV 或 FlashLoan 引起的价格过度变动
Solidity 中仅计算最近 1 小时的 TWAP
如果我们想要 1 小时的 TWAP,我们需要预计从现在起 1 小时后需要对累加器进行快照。
因此,我们需要访问公共变量 price0CumulativeLast 和公共函数 getReserves() 来获取上次更新时间,并对这些值进行快照。
function getReserves() public view returns (uint112 _reserve0, uint112 _reserve1, uint32 _blockTimestampLast) {
_reserve0 = reserve0;
_reserve1 = reserve1;
_blockTimestampLast = blockTimestampLast;
}
至少 1 小时后,我们可以调用并从 Uniswap V2 中获取最新的 price0CumulativeLast 值
以下代码为了说明目的而尽可能简单,不建议用于生产。
pragma solidity ^0.8.0;
import "@uniswap/v2-core/contracts/interfaces/IUniswapV2Pair.sol";
library UQ112x112 {
uint224 constant Q112 = 2**112;
// encode a uint112 as a UQ112x112
function encode(uint112 y) internal pure returns (uint224 z) {
z = uint224(y) * Q112; // never overflows
}
// divide a UQ112x112 by a uint112, returning a UQ112x112
function uqdiv(uint224 x, uint112 y) internal pure returns (uint224 z) {
z = x / uint224(y);
}
}
contract OneHourOracle {
using UQ112x112 for uint224; // requires importing UQ112x112
uint256 public snapshotPrice0Cumulative;
uint32 lastSnapshotTime;
function getTimeElapsed() internal view returns (uint32 t) {
unchecked {
t = uint32(block.timestamp % 2**32) - lastSnapshotTime;
}
}
function snapshot(IUniswapV2Pair uniswapV2pair) public {
require(getTimeElapsed() >= 1 hours, "snapshot is not stale");
// we don't use the reserves, just need the last timestamp update
(, , lastSnapshotTime) = uniswapV2pair.getReserves();
snapshotPrice0Cumulative = uniswapV2pair.price0CumulativeLast();
}
function getOneHourPrice(IUniswapV2Pair uniswapV2pair)
public
view
returns (uint256 twapPrice)
{
require(getTimeElapsed() >= 1 hours, "snapshot not old enough");
require(getTimeElapsed() < 3 hours, "price is too stale");
uint256 recentPriceCumul = uniswapV2pair.price0CumulativeLast();
uint256 timeElapsed = getTimeElapsed() - lastSnapshotTime;
unchecked {
twapPrice =
(recentPriceCumul - snapshotPrice0Cumulative) /
timeElapsed;
}
}
}
如果上次快照是三个小时前拍摄的怎么办?
如果与之交互的对在过去三个小时内没有交互,则上述合约将无法快照。
解决方案是让预言机在执行快照时调用 sync 函数,因为这将在内部调用。
// force reserves to match balances
function sync() external lock {
_update(IERC20(token0).balanceOf(address(this)), IERC20(token1).balanceOf(address(this)), reserve0, reserve1);
}
Reference
https://www.rareskills.io/post/twap-uniswap-v2
UniswapV2Library
UniswapV2库
Uniswap V2 库简化了一些与配对合约的交互,并被路由合约大量使用。
它包含八个不改变状态的函数。它们对于从智能合约集成 Uniswap V2 也很方便。
根据交易池输入计算输出 getAmountOut()
$$\Delta y = \frac{y r \Delta x}{x + r \Delta x}$$
UniswapV2 交易会抽取0.3%的手续费,作为提供流动性的奖励(计算恒定乘积的时候扣除手续费,但是交易池整体的余额增加,导致整体的乘积上涨,每笔交易都会让恒定乘积上涨。)
// given an input amount of an asset and pair reserves, returns the maximum output amount of the other asset
function getAmountOut(uint amountIn, uint reserveIn, uint reserveOut) internal pure returns (uint amountOut) {
require(amountIn > 0, 'UniswapV2Library: INSUFFICIENT_INPUT_AMOUNT');
require(reserveIn > 0 && reserveOut > 0, 'UniswapV2Library: INSUFFICIENT_LIQUIDITY');
uint amountInWithFee = amountIn.mul(997);
uint numerator = amountInWithFee.mul(reserveOut);
uint denominator = reserveIn.mul(1000).add(amountInWithFee);
amountOut = numerator / denominator;
}
根据交易池输出反推输入 getAmountIn()
$$\Delta x = \frac{x \Delta y}{r(y - \Delta y)}$$
// given an output amount of an asset and pair reserves, returns a required input amount of the other asset
function getAmountIn(uint amountOut, uint reserveIn, uint reserveOut) internal pure returns (uint amountIn) {
require(amountOut > 0, 'UniswapV2Library: INSUFFICIENT_OUTPUT_AMOUNT');
require(reserveIn > 0 && reserveOut > 0, 'UniswapV2Library: INSUFFICIENT_LIQUIDITY');
uint numerator = reserveIn.mul(amountOut).mul(1000);
uint denominator = reserveOut.sub(amountOut).mul(997);
amountIn = (numerator / denominator).add(1);
}
多个池子间连续兑换 getAmountsOut()
如果交易者提供一系列对: (A,B),(B,C),(C,D),预测输入 A 代币后输出的 D 代币数量
在 (A,B) 池中,将 A 代币作为输入,预估 B 代币的输出数量
在(B,C) 中,将 B 代币作为输入,预估 C 代币的输出数量
在(C,D) 中,将 C 代币作为输入,预估 D 代币的输出数量
// performs chained getAmountOut calculations on any number of pairs
function getAmountsOut(address factory, uint amountIn, address[] memory path) internal view returns (uint[] memory amounts) {
require(path.length >= 2, 'UniswapV2Library: INVALID_PATH');
amounts = new uint[](path.length);
amounts[0] = amountIn;
for (uint i; i < path.length - 1; i++) {
(uint reserveIn, uint reserveOut) = getReserves(factory, path[i], path[i + 1]);
amounts[i + 1] = getAmountOut(amounts[i], reserveIn, reserveOut);
}
}
多个池子间连续兑换 getAmountsIn()
如果交易者提供一系列对: (A,B),(B,C),(C,D),想要得到 D 代币,计算预估需要输入 A 代币的数量
在 (C,D) 池中,将 D 代币作为输出,预估 C 代币的输入数量
在(B,C) 中,将 C 代币作为输出,预估 B 代币的输入数量
在(A,B) 中,将 B 代币作为输出,预估 A 代币的输入数量
// performs chained getAmountIn calculations on any number of pairs
function getAmountsIn(address factory, uint amountOut, address[] memory path) internal view returns (uint[] memory amounts) {
require(path.length >= 2, 'UniswapV2Library: INVALID_PATH');
amounts = new uint[](path.length);
amounts[amounts.length - 1] = amountOut;
for (uint i = path.length - 1; i > 0; i--) {
(uint reserveIn, uint reserveOut) = getReserves(factory, path[i - 1], path[i]);
amounts[i - 1] = getAmountIn(amounts[i], reserveIn, reserveOut);
}
}
获取池子函数 pairFor 和 sortTokens
// returns sorted token addresses, used to handle return values from pairs sorted in this order
function sortTokens(address tokenA, address tokenB) internal pure returns (address token0, address token1) {
require(tokenA != tokenB, 'UniswapV2Library: IDENTICAL_ADDRESSES');
(token0, token1) = tokenA < tokenB ? (tokenA, tokenB) : (tokenB, tokenA);
require(token0 != address(0), 'UniswapV2Library: ZERO_ADDRESS');
}
// calculates the CREATE2 address for a pair without making any external calls
function pairFor(address factory, address tokenA, address tokenB) internal pure returns (address pair) {
(address token0, address token1) = sortTokens(tokenA, tokenB);
pair = address(uint(keccak256(abi.encodePacked(
hex'ff',
factory,
keccak256(abi.encodePacked(token0, token1)),
hex'96e8ac4277198ff8b6f785478aa9a39f403cb768dd02cbee326c3e7da348845f' // init code hash
))));
}
// fetches and sorts the reserves for a pair
function getReserves(address factory, address tokenA, address tokenB) internal view returns (uint reserveA, uint reserveB) {
(address token0,) = sortTokens(tokenA, tokenB);
(uint reserve0, uint reserve1,) = IUniswapV2Pair(pairFor(factory, tokenA, tokenB)).getReserves();
(reserveA, reserveB) = tokenA == token0 ? (reserve0, reserve1) : (reserve1, reserve0);
}
quote()
以当前价格为锚点,计算在特定价格的场景下,A 代币可以购买得到的 B 代币数量
// given some amount of an asset and pair reserves, returns an equivalent amount of the other asset
function quote(uint amountA, uint reserveA, uint reserveB) internal pure returns (uint amountB) {
require(amountA > 0, 'UniswapV2Library: INSUFFICIENT_AMOUNT');
require(reserveA > 0 && reserveB > 0, 'UniswapV2Library: INSUFFICIENT_LIQUIDITY');
amountB = amountA.mul(reserveB) / reserveA;
}
Reference
- https://www.rareskills.io/post/uniswap-v2-library
- https://github.com/Uniswap/v2-periphery/blob/master/contracts/libraries/UniswapV2Library.sol
UniswapV2 Routes
路由器合约为用户提供智能合约,用于
- 安全地铸造和销毁
LP代币(增加和减少流动性) - 安全地交换配对代币
- 通过与包装的
Ether (WETH) ERC20合约集成,增加了交换Ether的能力。 - 添加了核心合约中省略的与滑点相关的安全检查。
- 增加了对转移代币费用的支持。
uniswapRouter02 是 Router01 的附加功能,用于支持转账代币手续费。
SwapTokens-swapExactTokensForTokens
通过输入固定的代币,预估输出的代币数量
amountIn: 输入的源代币数量amountOutMin: 最小的代币输出数量,如果预估值小于该值,兑换报错回滚address[] calldata path: 代币地址数组,用于表示兑换路径to:接收输出代币的钱包地址deadline:交易完成的最晚时间
function swapExactTokensForTokens(
uint amountIn,
uint amountOutMin,
address[] calldata path,
address to,
uint deadline
) external override ensure(deadline) returns (uint[] memory amounts) {
amounts = UniswapV2Library.getAmountsOut(factory, amountIn, path);
require(amounts[amounts.length - 1] >= amountOutMin, 'UniswapV2Router: INSUFFICIENT_OUTPUT_AMOUNT');
TransferHelper.safeTransferFrom(path[0], msg.sender, UniswapV2Library.pairFor(factory, path[0], path[1]), amounts[0]);
_swap(amounts, path, to);
}
如果用户只交换两个代币,那么他们将向这些函数提供一个 address[] calldata path 数组 [address(tokenIn), address(tokenOut)]
如果他们跨池跳跃,他们将指定 [address(tokenIn), address(intermediateToken), …, address(tokenOut)]
SwapTokens-swapTokensForExactTokens
通过固定的代币输出数量,预估需要输入的源头代币数量
amountOut: 输出的目标代币数量amountInMax: 最大的代币输入数量,如果预估值大于该值,兑换报错回滚address[] calldata path: 代币地址数组,用于表示兑换路径to:接收输出代币的钱包地址deadline:交易完成的最晚时间
function swapTokensForExactTokens(
uint amountOut,
uint amountInMax,
address[] calldata path,
address to,
uint deadline
) external override ensure(deadline) returns (uint[] memory amounts) {
amounts = UniswapV2Library.getAmountsIn(factory, amountOut, path);
require(amounts[0] <= amountInMax, 'UniswapV2Router: EXCESSIVE_INPUT_AMOUNT');
TransferHelper.safeTransferFrom(path[0], msg.sender, UniswapV2Library.pairFor(factory, path[0], path[1]), amounts[0]);
_swap(amounts, path, to);
}
例如,假设想以 25 token0 swap 50 token1。
如果这是当前状态下的准确价格,则在交易确认之前价格变动将无法容忍,从而导致交易撤销。
因此,我们将最低价格指定为 49.5 token1,隐含地保留 1% 的滑点容忍度
兑换函数
先授权再兑换
大多数使用 EOA 的用户可能会选择使用精确输入功能,因为他们需要有一个批准步骤,如果他们需要输入超过他们批准的内容,交易就会失败
_swap() 函数
通过地址链路计算出每个池子的预估输出,作为 amounts 数组输入 _swap 函数
// requires the initial amount to have already been sent to the first pair
function _swap(uint[] memory amounts, address[] memory path, address _to) private {
for (uint i; i < path.length - 1; i++) {
(address input, address output) = (path[i], path[i + 1]);
(address token0,) = UniswapV2Library.sortTokens(input, output);
uint amountOut = amounts[i + 1];
(uint amount0Out, uint amount1Out) = input == token0 ? (uint(0), amountOut) : (amountOut, uint(0));
address to = i < path.length - 2 ? UniswapV2Library.pairFor(factory, output, path[i + 2]) : _to;
IUniswapV2Pair(UniswapV2Library.pairFor(factory, input, output)).swap(amount0Out, amount1Out, to, new bytes(0));
}
}
_addLiquidity()函数
还记得增加流动性的安全检查吗?
具体来说,我们要确保存入的两种代币的比例与该对当前的代币比例完全相同,否则我们铸造的 LP 代币数量就是我们提供的代币数量和该对余额之间的两个比率中较差的一个
然而,当流动性提供者试图增加流动性时和交易确认时,该比率可能会发生变化。
为了防止这种情况发生,流动性提供者必须提供(作为参数)他们希望为 token0 , token1 存入的最低余额(amountAMin和amountBMin)。
_addLiquidity 将获取 amountADesired 并计算符合该比率的正确 tokenB 数量。
如果此数量高于 amountBDesired(流动性提供者发送的 B 数量),则它将按照 amountBDesired 去计算 A 的最佳数量
function _addLiquidity(
address tokenA,
address tokenB,
uint amountADesired,
uint amountBDesired,
uint amountAMin,
uint amountBMin
) private returns (uint amountA, uint amountB) {
// create the pair if it doesn't exist yet
if (IUniswapV2Factory(factory).getPair(tokenA, tokenB) == address(0)) {
IUniswapV2Factory(factory).createPair(tokenA, tokenB);
}
(uint reserveA, uint reserveB) = UniswapV2Library.getReserves(factory, tokenA, tokenB);
if (reserveA == 0 && reserveB == 0) {
(amountA, amountB) = (amountADesired, amountBDesired);
} else {
uint amountBOptimal = UniswapV2Library.quote(amountADesired, reserveA, reserveB);
if (amountBOptimal <= amountBDesired) {
require(amountBOptimal >= amountBMin, 'UniswapV2Router: INSUFFICIENT_B_AMOUNT');
(amountA, amountB) = (amountADesired, amountBOptimal);
} else {
uint amountAOptimal = UniswapV2Library.quote(amountBDesired, reserveB, reserveA);
assert(amountAOptimal <= amountADesired);
require(amountAOptimal >= amountAMin, 'UniswapV2Router: INSUFFICIENT_A_AMOUNT');
(amountA, amountB) = (amountAOptimal, amountBDesired);
}
}
}
addLiquidity() 和 addLiquidityEth()
首先使用上面的方法计算最佳比率,_addLiquidity 然后将资产转移到池子,然后在池子中调用 mint。
唯一的区别是 addLiquidityEth 函数会先将 Ether 包装成 WETH。
消除流动性 removeLiquidity()
移除流动性调用销毁,但使用参数 amountAMin和amountBMin作为安全检查,以确保流动性提供者取回他们预期的代币数量。
function removeLiquidity(
address tokenA,
address tokenB,
uint liquidity,
uint amountAMin,
uint amountBMin,
address to,
uint deadline
) public override ensure(deadline) returns (uint amountA, uint amountB) {
address pair = UniswapV2Library.pairFor(factory, tokenA, tokenB);
IUniswapV2Pair(pair).transferFrom(msg.sender, pair, liquidity); // send liquidity to pair
(uint amount0, uint amount1) = IUniswapV2Pair(pair).burn(to);
(address token0,) = UniswapV2Library.sortTokens(tokenA, tokenB);
(amountA, amountB) = tokenA == token0 ? (amount0, amount1) : (amount1, amount0);
require(amountA >= amountAMin, 'UniswapV2Router: INSUFFICIENT_A_AMOUNT');
require(amountB >= amountBMin, 'UniswapV2Router: INSUFFICIENT_B_AMOUNT');
}
直接带着授权签名 add / remove Liquidity
UniswapV2 的 LP 代币是 ERC20 许可代币。该函数 removeLiquidityWithPermit() 接收签名以在一次交易中批准和销毁。
如果其中一个代币是 WETH,流动性提供者将使用 removeLiquidityETHWithPermit()
function removeLiquidityWithPermit(
address tokenA,
address tokenB,
uint liquidity,
uint amountAMin,
uint amountBMin,
address to,
uint deadline,
bool approveMax, uint8 v, bytes32 r, bytes32 s
) external override returns (uint amountA, uint amountB) {
address pair = UniswapV2Library.pairFor(factory, tokenA, tokenB);
uint value = approveMax ? uint(-1) : liquidity;
IUniswapV2Pair(pair).permit(msg.sender, address(this), value, deadline, v, r, s);
(amountA, amountB) = removeLiquidity(tokenA, tokenB, liquidity, amountAMin, amountBMin, to, deadline);
}
安全机制
切勿设置 amountMin = 0, amountMax = type(uint).max, 这会破坏针对价格滑点和夹层攻击的保护。
Router 合约提供了一种面向用户的机制,用于在多个池中交换具有滑点保护的代币,并增加了对交易 ETH 和转账费代币的支持。
Reference
https://www.rareskills.io/post/uniswap-v2-router
https://github.com/Uniswap/v2-periphery/blob/master/contracts/UniswapV2Router01.sol
Uniswap V3简介
本章节主要讲述了 Uniswap V3白皮书中的内容。同样,假设你没有理解本章的所有概念也没有关系,我们在后面章节直接看代码可能会更清晰。
为了更好地理解 UniswapV3 的创新之处在哪里,我们首先来看 UniswapV2 的缺点有哪些。
UniswapV2 使用 AMM 机制实现了一个通用的交易市场。 ·然而,并不是所有的交易对都是一样的,交易对可以根据价格的波动性分为以下两类:
- 价格波动性中等或较高的代币对。大多数代币对都属于这一类,因为绝大多数代币并没有锚定(
pegged to)到某些东西,因此其价格随着市场波动而波动。 - 价格波动性低的代币对。这一类包含了有锚定的代币,主要为稳定币
:USDT/USDC,USDC/DAI,USDT/DAI等等。也包括ETH/stETH,ETH/rETH(一些wrapped ETH)等类型。
这些不同的代币对,对于流动性池的配置有不同的要求。最主要的区别在于,锚定代币对需要非常高的流动性来降低大额交易对其价格的影响。但是 USDC,USDT 的价格必须保持在1附近,无论我要买卖多大数目的代币。由于 UniswapV2 的通用 AMM 算法对于稳定币交易并没有很好的适配,所以在稳定币的交易中其他的 AMM(主要是Curve)更加流行。
导致这个问题出现的原因是,UniswapV2 池子的流动性是分布在无穷区域上的——池子允许在任何价格的交易发生,从 0 到正无穷 ${+ \infty}$:
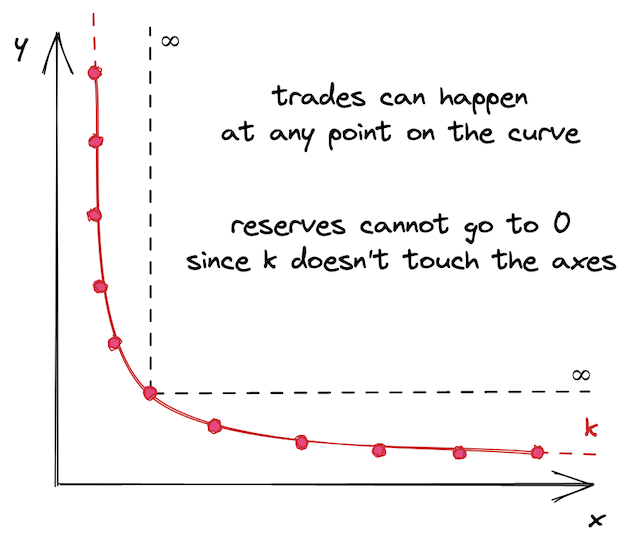
这听起来好像不是一个坏事,但事实上它导致了资产利用效率的不足。一个资产的历史价格通常是在某个区间内的,不管这个区间是大还是小。
比如,ETH 的历史价格大致在 1990 ~2100 这个区间(数据来源 CoinMarketCap)。
在今天(2025年3月),1 个 ETH 的现货价格是 1991 ,没有人会愿意用 5000 购买一个 ETH,所以在这个价格上提供流动性是毫无用处的。因此,在远离当前价格区间的、永远不会达到的某个点上提供流动性是毫无意义的。
集中流动性-提高资金利用率
UniswapV3 引入了 集中流动性(concentrated liquidity) 的概念:
LP 可以选择他们希望在哪个价格区间提供流动性。
这个机制通过将更多的流动性提供在一个相对狭窄的价格区间,来大大提高资产利用效率;
这也使 Uniswap 的使用场景更加多样化:它现在可以对于不同价格波动性的池子进行不同的配置。
这就是 V3 相对于 V2 的主要提升点。
简单地来说,一个 UniswapV3 的交易对由许多个 UniswapV2 的交易对构成。
V2 与 V3 的区别是:
- 在
V3中,一个交易对有许多的价格区间,而每个价格区间内都有一定数量的资产。从零到正无穷的整个价格区间被划分成了许多个小的价格区间,每一个区间中都有一定数量的流动性。 - 而更关键的点在于,在每个小的价格区间中,工作机制与 UniswapV2 完全一样。这也是为什么我们说一个
UniswapV3的池子就是许多个V2的池子。
下面,我们来对这种机制进行可视化。我们并不是重新选择一个有限的曲线,而是我们把它在价格 $a$ 与价格 $b$ 之间的部分截取出来,把它们当作是是曲线的边界。更进一步,我们把曲线进行平移使得边界点落在坐标轴上,于是得到了下图:
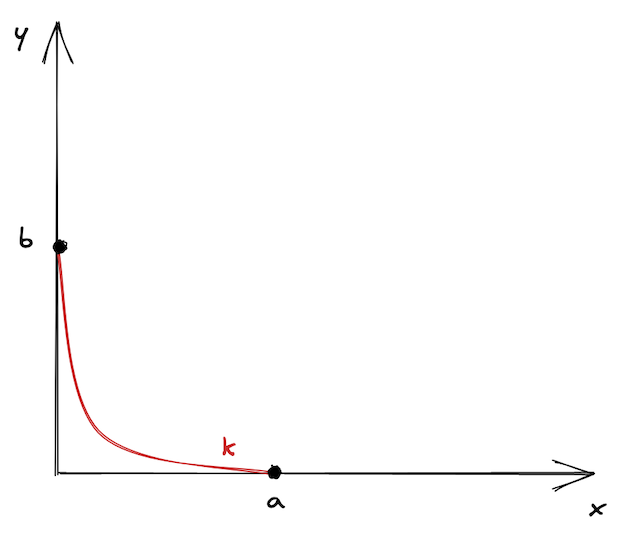
它看起来或许有点单调, 因此 UniswapV3 有许多的价格区间——这样它们就不会感到孤单了 🙂
正如我们在前一章中讲到的那样,交易 token 使得价格在曲线上移动,而价格区间限制了价格点的移动。当价格移动到曲线的一端时,我们说这个池子被耗尽了:其中一种代币的资产变成了 0,无法再购买这种代币(当然,仅仅指在这个价格区间内)。
假设起始价格在上图中曲线的中间一点。为了到达点 $a$,我们需要购买池子里所有的 $y$ 来使得池子里的 $x$ 最大化;为了到达点 $b$,我们需要买光池子里的 $x$ 从而使 $y$ 最大化。在这两个点,池子里都只剩一种 token。
一个有趣的事实:根据这个原理,可以利用V3的价格区间来挂限价单。
如果当前价格区间池子被耗尽将会发生什么?价格点会滑动到下一个价格区间。如果下一个价格区间不存在,这笔交易就会以部分成交而结束——我们将在本书后面的部分看到其如何实现。
下面一图展示了 USDC/ETH 池子的流动性分布:
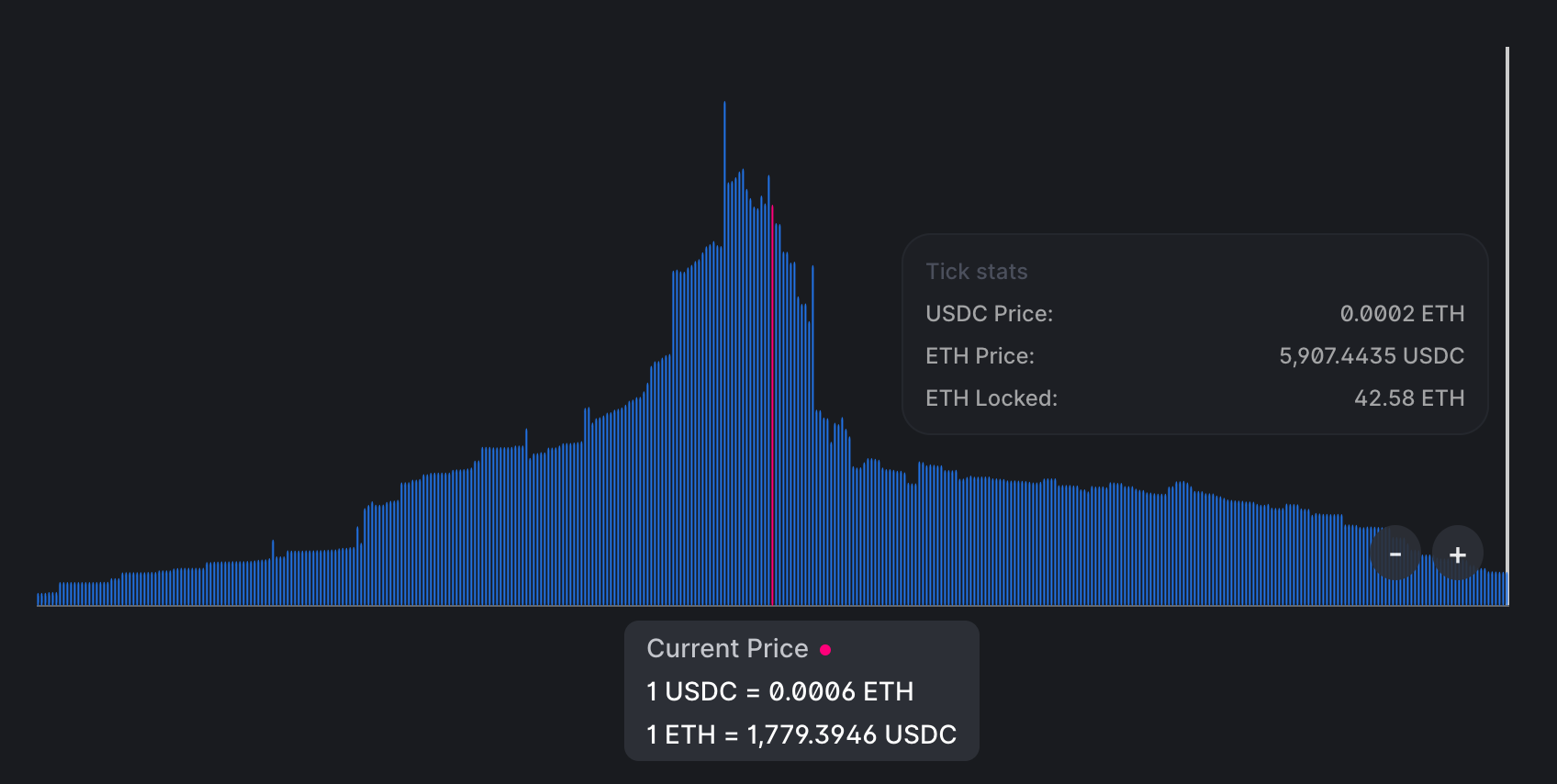
可以看到,大量流动性集中在现价的附近,而较远的价格区间中的流动性较少——
这是因为 LP 更希望提高它们的资产利用效率。当然,整个区间也不是无穷的,在图片右侧也显示了其上界。
Uniswap V3 的数学原理
在数学原理上,V3 是基于 V2 的:它们使用了相同的底层公式,但实际上 V3 使用的是增强版。
为了处理价格区间之间的转换,简化流动性管理,以及避免取整出现问题,V3 使用了下面这些新的标识:
$$L = \sqrt{xy}$$
$$\sqrt{P} = \sqrt{\frac{y}{x}}$$
$L$ 被称作 流动性数量。池子中的流动性是两种 token 资产数量的组合。我们知道,按照公式,两种代币数量乘积为 $k$,因此我们可以用 $\sqrt{xy}$ 来衡量池子流动性。$L$ 实际上是 $x$ 和 $y$ 的几何平均数。
$y/x$ 是 token0 相对于 token1 的价格。由于池子里两种代币的价格互为倒数,我们在计算中仅使用其中一个( Uniswap V3使用的是 $y/x$)。token1 相对于 token0 的价格即为 $\frac{1}{y/x}=\frac{x}{y}$。类似地, $\frac{1}{\sqrt{P}} = \frac{1}{\sqrt{y/x}} = \sqrt{\frac{x}{y}}$.
我们使用 $\sqrt{P}$ 而不是 $P$ 有两个原因:
-
平方根计算并不精确并且会引入取整的问题。因此,更简单的方法是我们干脆就在合约中存平方根的结果,而不是在合约中计算它。(合约中并不存储 $x$ 和 $y$ )
-
$\sqrt{P}$ 与 $L$ 之间有一个有趣的关系:$L$ 也表示了输出数量的变化与 $\sqrt{P}$ 的变化之间的关系:
$L = \frac{\Delta y}{\Delta\sqrt{P}}$
证明: $L = \frac{\Delta y}{\Delta\sqrt{P}}$
$$\sqrt{xy} = \frac{y_1 - y_0}{\sqrt{P_1} - \sqrt{P_0}}$$
$$\sqrt{xy} (\sqrt{P_1} - \sqrt{P_0}) = y_1 - y_0$$
$$\sqrt{xy} (\sqrt{\frac{y_1}{x_1}} - \sqrt{\frac{y_0}{x_0}}) = y_1 - y_0$$
$$\sqrt{y_1^2} - \sqrt{y_0^2} = y_1 - y_0$$
$$y_1 - y_0 = y_1 - y_0$$
(译者注:第四步到第五步,$\sqrt{xy} = \sqrt{x_0y_0} = \sqrt{x_1y_1}$ )
价格
同样,我们并不需要计算准确的价格——我们可以直接计算获得的 token 数量。并且,由于我们在合约中并不存储 $x$ 和 $y$,我们将仅通过 $L$ 和 $\sqrt{P}$ 进行计算。
根据上文中的公式,我们能得到 $\Delta y$:
$$\Delta y = \Delta \sqrt{P} L$$
见上述证明中的第三步。
正如上面所说,双方的价格互为倒数。因此,$\Delta x$ 的公式为:
$$\Delta x = \Delta \frac{1}{\sqrt{P}} L$$
$L$ 和 $\sqrt{P}$ 让我们不再需要存储和更新池子资产数量。并且,我们也并不需要每次都重新计算 $\sqrt{P}$ 因为我们从上述公式可以得到 $\Delta \sqrt{P}$。
Ticks
正如我们前面说到的,V2 中的无穷价格区间在 V3 中被分成了更小的价格区间,每个区间都由上下界端点进行限制。为了进行这些边界的协调,V3 引入了 ticks。
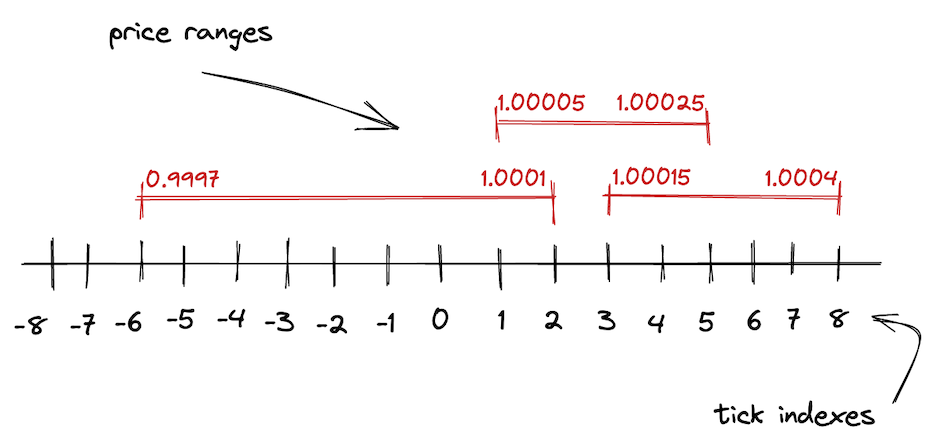
在 V3,整个价格区间由离散的、均匀分布的 ticks 进行标定。每个 tick 有一个 index 和对应的价格:
$$p(i) = 1.0001^i$$
$p(i)$ 即为 tick $i$ 的价格. 使用 1.0001 的幂次作为标定有一个很好的性质:两个相邻 tick 之间的差距为 0.01% 或者一个基点。
基点 (1% 的百分之一,或者 0.01%,或者 0.0001)是在金融中用来衡量百分比的一个单位。你可能在央行宣布对于利率的调整中听过基点这个名词。
正如我们之前讨论的,UniswapV3 存储的是 $\sqrt{P}$ 而不是 $P$。所以这个公式实际上是:
$$\sqrt{p(i)} = \sqrt{1.0001}^i = 1.0001 ^{\frac{i}{2}}$$
我们得到的值大概是这样:$\sqrt{p(0)} = 1$, $\sqrt{p(1)} = \sqrt{1.0001} \approx 1.00005$, $\sqrt{p(-1)} \approx 0.99995$.
Ticks 可以为正也可以为负,并且显然它不是无穷的。
V3 把$\sqrt{P}$ 存储为一个 Q64.96 类型的定点数,使用 64 位作为整数部分,使用 96 位作为小数部分。因此,价格的取值范围是 $[2^{-128}, 2^{128}]$,ticks 的取值范围是:
$$[log_{1.0001}2^{-128}, log_{1.0001}{2^{128}}] = [-887272, 887272]$$
如果希望对于 Uniswap V3 的数学原理有更深的理解,推荐这篇技术文章,作者为 Atis Elsts
开发环境
本书中,我们会搭建两个应用:
- 链上:一套部署在以太坊上的智能合约
- 链下:一个与智能合约交互的前端应用
尽管本书把前端应用作为其中一部分,但这不是我们的主要关注点。我们搭建前端仅仅为了展示智能合约是如何集成到前端应用中的。因为,前端部分是选读内容,但在本书代码仓库中也提供了这部分的代码。
以太坊简介
以太坊是一个允许任何人在上面运行应用的区块链。它与一个传统云服务的主要区别在于:
- 维持这个应用不需要付费,部署应用需要付费;
- 应用代码是不可变的,在其部署后你没有办法再进行修改;
- 用户调用你的应用需要花费 gas(手续费);
为了更好地理解这些区别,我们来看一下以太坊的构成。
以太坊的核心(其他区块链也是同理)是一个数据库。这个数据库中最有价值的数据是账户状态。以太坊中的每个账户包含一个地址,以及以下数据:
- 余额:账户的以太坊(ether)余额
- 代码:部署在这个地址上的智能合约的字节码
- 存储:智能合约存储数据的空间
- nonce:一个用来防止重放攻击的整数序号
(译者注:Ethereum 和 ether 的中文译名均为以太坊,读者注意区分。Ethereum 指的是这条区块链,ether 指的是该链上的原生代币 ETH)
以太坊的主要任务是安全地维护这些数据,防止它们被未经授权的操作更改。
同时,以太坊也是一个网络,网络中的每个计算机都独立地构建和维持这些状态。网络的主要目标是能够去中心化地访问数据库:没有任何单个权威机构可以单方面修改任何数据。这是通过叫做共识的机制来实现的,即网络中节点遵守的一系列规则。如果有节点违反了规则,它将会被从这个网络中排除。
有趣的是,区块链也可以使用 MySQL!只是可能会存在一定的性能问题。以太坊中使用的是 LevelDB,一个高效的 KV 数据库。
每个以太坊节点运行 EVM,以太坊虚拟机。虚拟机是一个能够执行其他程序的程序,EVM 则是执行智能合约程序的程序。用户通过交易(transactions)与合约交互,除了能够简单的发送 ether,交易也能够调用智能合约,需要传输的数据包括:
- 一个合约函数的签名
- 函数参数
交易被打包进区块,区块被矿工挖出。网络中的每个节点都可以验证每一个区块中的每一笔交易。
某种意义上来说,智能合约与 JSON APIs 有一定类似,区别就是你调用的是智能合约函数。与 API 的后端类似,智能合约也执行程序逻辑,并且也可能更改智能合约中存储的数据。而与 API 不同的是,你需要发送一笔交易来改变区块链的状态,并且你需要为每一笔交易付费。
最后,以太坊节点也实现了一套 JSON-RPC API。我们可以通过这个 API 与节点进行交互:获取账户余额、估算 gas 费、获取区块和交易、发送交易、执行不上链的智能合约调用(仅能读数据)。在这里你可以获得一个可用节点的列表。
交易也是通过这个 API 发送的, 参见 eth_sendTransaction.
本地开发环境
我们将要搭建智能合约并且在以太坊上运行它们,这意味着我们需要一个节点。在本地测试和运行合约也需要一个节点。曾经这使得智能合约开发十分麻烦,因为在一个真实节点上运行大量的测试会十分缓慢。不过现在已经有了很多快速简洁的解决方案。例如 Truffle 和 Hardhat。不过这些工具的问题在于我们需要用 JavaScript 来写测试以及与区块链的交互,这是因为 Truffle 和 Hardhat 都运行了一个本地节点,并且使用 JavaScript 的 Web3 库来与节点交互。
我们将会选择一个新的框架,Foundry。
Foundry
Foundry 是一套用于以太坊应用开发的工具包。我们将会使用以下这些工具:
Forge 使智能合约开发更加容易。当使用 Forge 开发时,我们不需要运行一个本地节点来进行测试;Forge 会在其内置的 EVM 上运行测试:这大大加快了开发速度,让我们不再需要给节点发送交易和挖出区块。除此以外,Forge 还能够使用 Solidity 编写测试!Forge 也内置了一些机制方便我们模拟区块链的各种状态:修改某个账户余额,从其他地址执行合约,把合约部署在任意地址等等。
然而,我们仍然需要一个本地节点来部署合约。在这里我们将会使用 Anvil。前端应用可以使用 JavaScript 的库来与以太坊节点进行交互。
Ethers.js
Ethers.js 是一个与 Ethereum 交互的 JavaScript 库. 这是 Dapp 开发中使用的两个最流行的 JS 库之一(另一个是 web3.js)。这些库让我们可以使用 JSON-API 与以太坊节点交互,并且也有各种功能丰富的函数来帮助开发者更容易地开发应用。
MetaMask
MetaMask 是一个浏览器中的以太坊钱包。它是一个浏览器插件,可以安全地创建和存储私钥。Metamask 也是最常用的以太坊钱包应用,我们将使用它来与我们的本地运行的节点进行交互。
React
React 是前端开发中使用的一个著名的 JS 库. 本书并不要求会 React,我们将会提供一个模板。
准备开发环境
创建一个新的文件夹,并在其中运行 forge init :
$ mkdir uniswapv3clone
$ cd uniswapv3clone
$ forge init
如果你使用 Visual Studio Code 进行开发,可以在
forge init中加入--vscode这个flas:forge init --vscode。Forge 会在初始化时对于 VSCode 进行特别设置。
Forge会在 src, test, 和 script 创建样例合约,这些都可以删掉。
设置前端开发环境:
$ npx create-react-app ui
第一笔交易
在本章中,将会搭建一个流动性池合约,它能够接受用户的流动性并且在某个价格区间内做交易。
简单起见,我们仅在一个价格区间内提供流动性,并且仅允许单向的交易。
另外,为了更好地理解其中的数学原理,我们将手动计算其中用到的数学参数,暂不使用 Solidity 的数学库进行计算。
我们本章中要搭建的模型如下:
- 这是一个
ETH/USDC的池子合约。ETH是资产 $x$,USDC是资产 $y$; - 现货价格将被设置为一个
1 ETH, 5000 USDC; - 我们提供流动性的价格区间为一个ETH对
4545 - 5500 USDC; - 我们将会从池子中购买
ETH,并且保证价格在上述价格区间内。
模型的图像大致如下:
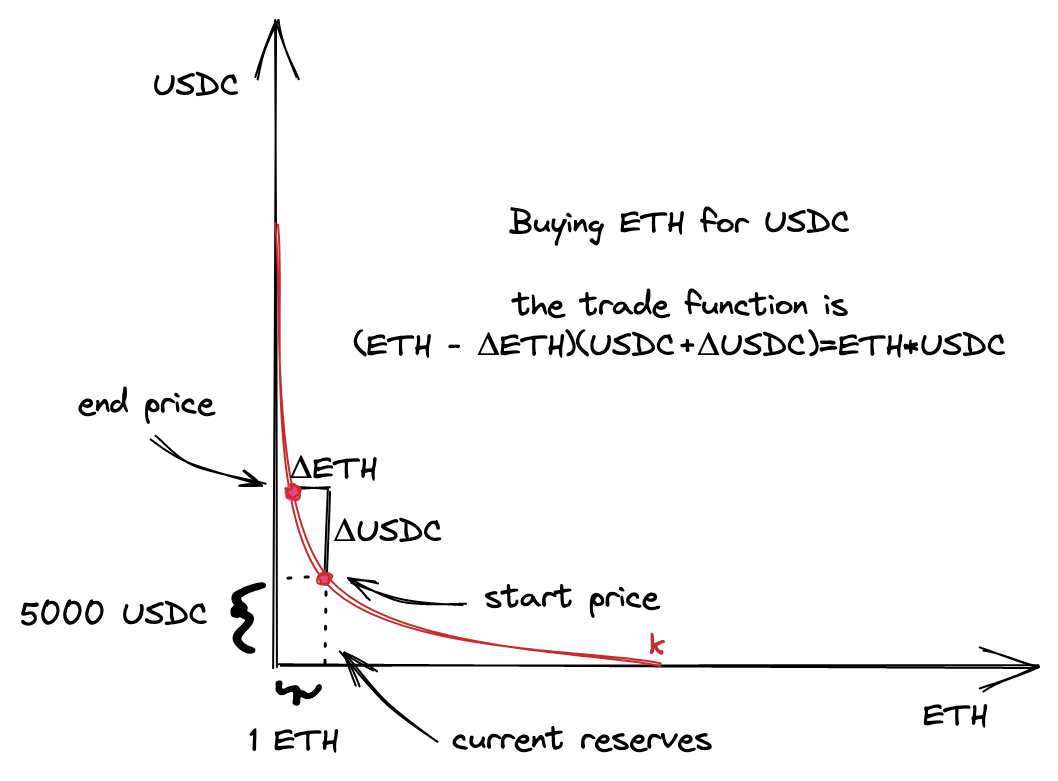
在开始代码部分之前,我们首先会手动计算模型中用到的所有数学参数。
简单起见,我将使用 Python 来进行计算而不是 Solidity,因为 Solidity 在数学计算上有很多细微之处需要考虑。
因此在这章,我们将会把所有的参数硬编码进池子合约里。这会让我们获得一个最小可用的产品。
完整的合约代码
计算流动性
没有流动性就无法进行交易。为了能够完成我们的第一笔交易,我们首先需要向池子中添加一些流动性。 而为了向池子合约添加流动性,我们需要知道:
- 一个价格区间,即
LP希望他的流动性仅在这个区间上提供和被利用; - 提供流动性的数量,也即提供的两种代币的数量,我们需要将它们转入池子合约。
在本节中,我们会手动计算上述变量的值;在后续章节中,我们会在合约中对此进行实现。
首先我们来考虑价格区间。
价格区间计算
回忆一下上一章所讲,在 UniswapV3 中,整个价格区间被划分成了 ticks:
每个 tick 对应一个价格,以及有一个下标。
在我们的第一个实现中,我们的现货价格设置为 1 ETH , 5000 USDC。
- 购买
ETH会移除池子中的一部分ETH,从而使得ETH价格变得高于5000 USDC - 提供流动性的用户希望在一个包含此价格的区间中提供流动性,并且要确保最终的价格落在这个区间内。(跨区间的交易将会在后续章节提到)。
我们需要找到 价格区间上下限分别对应的 tick:
- 对应现货价格的
tick(1 ETH , 5000 USDC) - 提供流动性的价格区间上下界对应的
tick
- 在这里,下限为
4545 USDC - 上限为
5500 USDC
从之前的章节中我们知道下述公式:
$$ P = \frac{y}{x} = (1.0001)^{i}$$
$$i = log_{1.0001} P(i)$$
由于我们把 ETH 作为资产 $x$,USDC 作为资产 $y$,每个 tick 对应的值为:
$$ P_c = \frac{5000}{1} = 5000$$
$$P_l = \frac{4545}{1} = 4545$$
$$P_u = \frac{5500}{1} = 5500$$
在这里,$P_c$ 代表现货价格,$P_l$ 代表区间下界,$P_u$ 代表区间上界。
接下来,我们可以计算价格对应的 ticks。使用下面公式:
- 现价 tick: $i_c = log_{1.0001} 5000 \approx 85176$
- 下界 tick: $i_l = log_{1.0001} 4545 \approx 84222$
- 上界 tick: $i_u = log_{1.0001} 5500 \approx 86129$
上述计算使用的是 Python:
import math def price_to_tick(p): return math.floor(math.log(p, 1.0001)) price_to_tick(5000) > 85176
价格区间的计算就是这样。
V3 把$\sqrt{P}$ 存储为一个 Q64.96 类型的定点数,使用 64 位作为整数部分,使用 96 位作为小数部分。因此,价格的取值范围是 $[2^{-128}, 2^{128}]$
在我们上面的计算中,价格按照浮点数形式计算。我们需要将价格的平方根转换成 Q64.96 格式,也非常简单:只需要将这个数乘以 $2^{96}$,即可得到:
$$\sqrt{P_c} = \sqrt{5000} * 2 ^{96} = 5602277097478614198912276234240$$
$$\sqrt{P_l} = \sqrt{4545} * 2 ^{96} = 5314786713428871004159001755648$$
$$\sqrt{P_u} = \sqrt{5500} * 2 ^{96} = 5875717789736564987741329162240$$
在 Python 中:
q96 = 2**96 def price_to_sqrtp(p): return int(math.sqrt(p) * q96) price_to_sqrtp(5000) > 5602277097478614198912276234240注意先进行乘法再取整,否则会损失精度
Token 数量计算
接下来,我们需要决定向池子中投入多少 token。
答案是:越多越好。数量并没有严格定义,我们质押的数目越多,购买同样数量的 ETH 就会使得价格的变动越小,防止离开我们的价格区间。
在开发和测试智能合约的过程中,我们可以获得任意数量的 token,所以钱不是问题。
为了实现我们的第一笔交易,我们将会在池子中质押 1 ETH , 5000 USDC
要记得池子中资产数量的比例决定了现货价格。所以假设我们希望像池子中投入更多的资产而保持现货价格不变,我们投入的资产也必须满足同样的比例,例如:2 ETH 和 10,000 USDC;10 ETH 和 50,000 USDC。
流动性数量计算
接下来,我们将基于我们质押 token 的数量计算流动性 $L$ 的值。
根据之前我们提到过的公式,流动性数量如下计算:
$$L = \sqrt{xy}$$
然而,上述公式是用于无穷价格区间曲线,但我们希望的是把流动性放在某个有界的价格区间,也即无穷曲线的一部分。 我们需要针对我们希望流动性存在的价格区间来计算对应的 $L$,因此可能需要一些更复杂的计算。
为了计算这个价格区间的 $L$,我们来回顾我们之前讨论过的一个有趣的点:
价格区间可以被耗尽。
我们可以将一个价格区间的某种 token 全部买走,使得该区间中只有另一种 token:
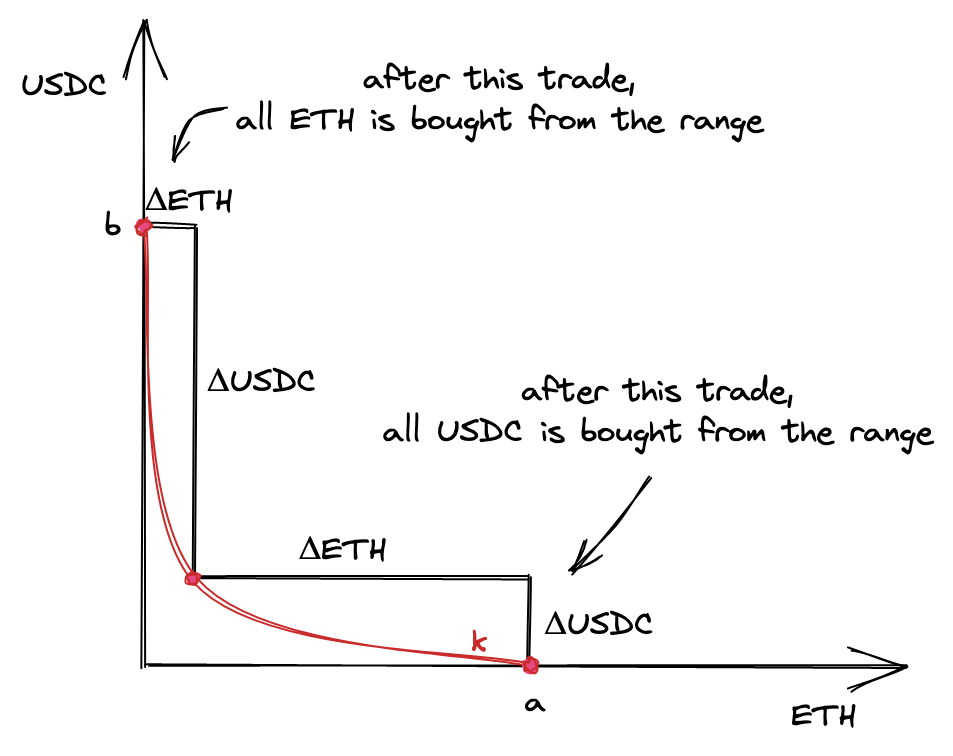
在上图中的两个边界点,区间流动性池中都只有一种 token:
在 $a$ 点池子里只有 ETH,在 $b$ 点只有 USDC。
也就是说,我们希望能够找到一个 $L$,使得价格能够移动到两个端点处。 我们需要足够的流动性来使得价格能够达到上下界,因此,我们会希望通过 $\Delta x$ 和 $\Delta y$ 的最大值来计算流动性。
现在我们来看一下边界点的价格。当从池子中购买 ETH 时,池子中的 ETH 减少,ETH 的价格会升高;
当从池子中使用 ETH 购买 USDC时,池子中的 ETH 数量会增加,同时 ETH 的价格会下跌。
由于价格为 $\frac{y}{x}$,所以 $a$ 点为价格最低点,$b$ 点为价格最高点。
事实上,按照公式,在这两个点的价格是没有定义的,因为池子中只有一种 token,但是我们在这里只需要理解,$b$ 点的价格高于起始价格,$a$ 点价格低于起始价格即可。
现在,我们将图中的曲线分为两部分:起始点左边和起始点右边。
我们将在两边分别计算出 $L$。
为什么会有两个?
这是因为,在交易过程中,价格会朝着某个方向移动:升高或降低。对于价格的移动,仅有一种 token 会起作用:
左半边由 token $x$ 随着价格升高不断减少,右半边由 token $y$ 随着价格升高也是不断减少
- 当
token x价格升高时,表示池子中的token x的数量减少,因此推高token x价格的交易大多应该是从池子中购买token x - 当
token x价格下降时,表示池子中的token x的数量增加,因此降低token x价格的交易大多应该是从池子中购买token y,往池子中注入更多的token x
因此,导致价格升到左半边顶点 b 的交易应该是通过用户不断购入 token x 提供,因此只通过 token x 数量计算出来
类似地,导致价格降到右半边低点 a 的交易应该是通过用户不断购入 token y 提供,因此只通过 token y 数量计算出来
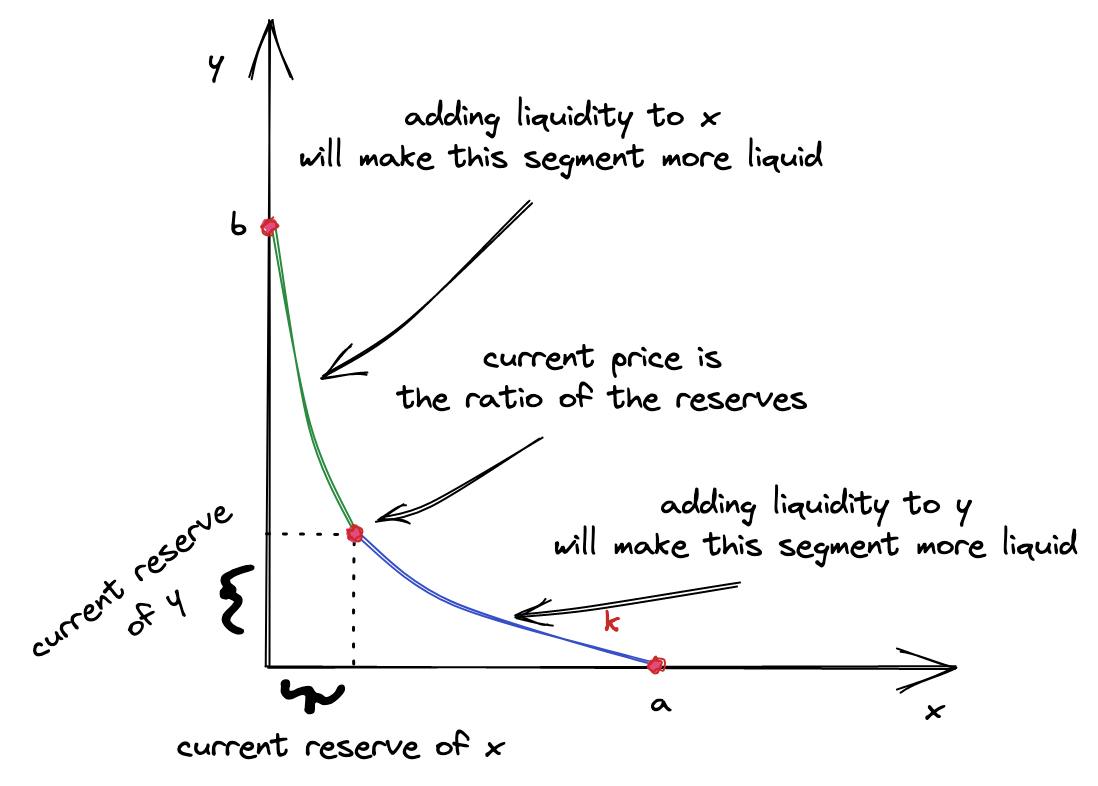
这也是为什么,我们会计算出两个不同的 $L$ 并选择其中一个。
选择哪个呢?
选择较小的值。因为较大的那个流动性包含了较小的流动性。我们希望流动性均匀分布在我们所提供的价格区间中,因此左右提供的流动性需要保持一致。如果我们选择较大的那个,用户所提供的某种 token 的数量可能会大于其指定的数量,来平衡两边的流动性。这的确理论上是可行的,但是会让整个智能合约变得更加复杂。
那么,较大的 $L$ 怎么办呢?实际上是没有用的。我们挑选小的那个 $L$,并且计算出这个 $L$ 对应的较大的 $L$ 那边 token 的数量——会比之前的要小。这样,两边的流动性就相同了,都等于较小值。
最后还需要说明的一个关键点是:新的流动性需要保证不改变现货价格。也即,它必须与现在两种资产的数量成比例。这也是为什么我们上面会计算出两个 $L$ ——因为仅考虑了一种资产,而没有保证比例。我们选择较小的那个 $L$ 来重新计算比例。
上面的说明有些绕,或许在后面实现代码的过程中我们会对此理解更清晰吧。现在我们来看公式。
回忆一下, $\Delta x$ 和 $\Delta y$ 的计算公式为:
$$\Delta x = \Delta \frac{1}{\sqrt{P}} L$$ $$\Delta y = \Delta \sqrt{P} L$$
我们把上述公式中的 $\Delta \sqrt{P}$ 相关部分展开:
$$\Delta x = (\frac{1}{\sqrt{P_c}} - \frac{1}{\sqrt{P_b}}) L$$ $$\Delta y = (\sqrt{P_c} - \sqrt{P_a}) L$$
$P_a$ 是 $a$ 点的价格,$P_b$ 是 $b$ 点的价格, $P_c$ 是现货价格。
我们接下来根据第一个公式推导出计算 $L$ 的公式:
$$\Delta x = (\frac{1}{\sqrt{P_c}} - \frac{1}{\sqrt{P_b}}) L$$ $$\Delta x = \frac{L}{\sqrt{P_c}} - \frac{L}{\sqrt{P_b}}$$ $$\Delta x = \frac{L(\sqrt{P_b} - \sqrt{P_c})}{\sqrt{P_b} \sqrt{P_c}}$$ $$L = \Delta x \frac{\sqrt{P_b} \sqrt{P_c}}{\sqrt{P_b} - \sqrt{P_c}}$$
从第二个公式推导: $$\Delta y = (\sqrt{P_c} - \sqrt{P_a}) L$$ $$L = \frac{\Delta y}{\sqrt{P_c} - \sqrt{P_a}}$$
这就是我们的两个 $L$ 的计算公式,跟别对应起始点两边的两段曲线:
$$L = \Delta x \frac{\sqrt{P_b} \sqrt{P_c}}{\sqrt{P_b} - \sqrt{P_c}}$$ $$L = \frac{\Delta y}{\sqrt{P_c} - \sqrt{P_a}}$$
接下来,我们把之前计算出的价格代入公式:
$$L = \Delta x \frac{\sqrt{P_b}\sqrt{P_c}}{\sqrt{P_b}-\sqrt{P_c}} = 1 ETH * \frac{\sqrt{5500} * \sqrt{5000}}{\sqrt{5500} - \sqrt{5000}}$$ 转换成 Q64.96 后得到:
$$L = 1519437308014769733632$$
对于另一个 $L$: $$L = \frac{\Delta y}{\sqrt{P_c}-\sqrt{P_a}} = \frac{5000USDC}{\sqrt{5000} - \sqrt{4500}}$$ $$L = 1517882343751509868544$$
两者中,我们选择小的那一个
Python 计算:
sqrtp_low = price_to_sqrtp(4545) sqrtp_cur = price_to_sqrtp(5000) sqrtp_upp = price_to_sqrtp(5500) def liquidity0(amount, pa, pb): if pa > pb: pa, pb = pb, pa return (amount * (pa * pb) / q96) / (pb - pa) def liquidity1(amount, pa, pb): if pa > pb: pa, pb = pb, pa return amount * q96 / (pb - pa) liq0 = liquidity0(amount_eth, sqrtp_cur, sqrtp_upp) liq1 = liquidity1(amount_usdc, sqrtp_cur, sqrtp_low) liq = int(min(liq0, liq1)) > 1517882343751509868544
重新计算 token 数量
尽管我们初始选择了我们想要质押的 token 数目,这个数目可能并不准确。
我们并不能在任何价格区间质押任何比例的 token 来获取流动性,因为流动性需要满足在价格区间的曲线上均匀分布。
因此,尽管用户选择了起始数量,合约会对它们重新计算,所以实际的数量会略有不同(至少会有取整的精度问题)
幸运的是,我们已经获得了对应的公式:
$$\Delta x = \frac{L(\sqrt{P_b} - \sqrt{P_c})}{\sqrt{P_b} \sqrt{P_c}}$$ $$\Delta y = L(\sqrt{P_c} - \sqrt{P_a})$$
在 Python 中:
def calc_amount0(liq, pa, pb): if pa > pb: pa, pb = pb, pa return int(liq * q96 * (pb - pa) / pa / pb) def calc_amount1(liq, pa, pb): if pa > pb: pa, pb = pb, pa return int(liq * (pb - pa) / q96) amount0 = calc_amount0(liq, sqrtp_upp, sqrtp_cur) amount1 = calc_amount1(liq, sqrtp_low, sqrtp_cur) (amount0, amount1) > (998976618347425408, 5000000000000000000000)正如上述计算结果,得到的数据基本等于我们想要提供的数量,不过 ETH 略少一点
Hint: 使用
cast --from-wei AMOUNT来把wei转换成ether, 示例:
cast --from-wei 998976618347425280输出0.998976618347425280.
提供流动性
池子合约
正如我们在简介中提到的,Uniswap 部署了多个池子合约,每一个负责一对 token 的交易。
Uniswap 的所有合约被分为以下两类:
- 核心合约(
core contracts) - 外部合约(
periphery contracts)
正如其名,核心合约实现了核心的逻辑。这些合约是最小的,对用户不友好的,底层的合约。 这些合约都只做一件事并且保证这件事尽可能地安全。
在 UniswapV3 中,核心合约包含以下两种:
- 池子(
Pool)合约,实现了去中心化交易的核心逻辑 - 工厂(
Factory)合约,作为池子合约的注册入口,使得部署池子合约更加简单。
我们将会从池子合约开始,这部分实现了 Uniswap 99% 的核心功能。
创建 src/UniswapV3Pool.sol:
pragma solidity ^0.8.14;
contract UniswapV3Pool {}
首先我们需要明确的是:
UniswapV3是基于ticks对应的价格区间创建的交易对池子- 每个池子都在自己的
ticks对应的价格区间内提供流动性 - 同样的
ticks价格区间,可能会存在多个池子在提供流动性
设计合约需要存储哪些数据:
- 存储
token交易对地址。这些地址是静态的,仅设置一次并且保持不变的(因此,这些变量需要被设置为immutable); - 每个池子合约包含了一系列的流动性位置,我们需要用一个
mapping来存储这些信息,key代表不同位置,value是包含这些位置相关的信息; - 存储池子
tick信息,标识当前池子提供流动性的价格区间; - 池子的
tick的范围是固定的,这些范围在合约中存为常数; - 需要存储池子流动性的总数 $L$;
- 跟踪现在的价格和对应的
tick,把他们存储在一个slot中来节省gas费, Solidity 变量在存储中的分布特点
总之,合约大概存储了以下这些信息:
// src/lib/Tick.sol
library Tick {
struct Info {
bool initialized;
uint128 liquidity;
}
...
}
// src/lib/Position.sol
library Position {
struct Info {
uint128 liquidity;
}
...
}
// src/UniswapV3Pool.sol
contract UniswapV3Pool {
using Tick for mapping(int24 => Tick.Info);
using Position for mapping(bytes32 => Position.Info);
using Position for Position.Info;
int24 internal constant MIN_TICK = -887272;
int24 internal constant MAX_TICK = -MIN_TICK;
// Pool tokens, immutable
address public immutable token0;
address public immutable token1;
// Packing variables that are read together
struct Slot0 {
// Current sqrt(P)
uint160 sqrtPriceX96;
// Current tick
int24 tick;
}
Slot0 public slot0;
// Amount of liquidity, L.
uint128 public liquidity;
// Ticks info
mapping(int24 => Tick.Info) public ticks;
// Positions info
mapping(bytes32 => Position.Info) public positions;
...
UniswapV3 有很多辅助的合约,Tick 和 Position 就是其中两个。
接下来,我们在 constructor 中初始化其中一些变量:
constructor(
address token0_,
address token1_,
//当前价格
uint160 sqrtPriceX96,
int24 tick // 当前价格所对应的 tick index
) {
token0 = token0_;
token1 = token1_;
slot0 = Slot0({sqrtPriceX96: sqrtPriceX96, tick: tick});
}
}
在构造函数中,初始化了不可变的 token 交易对地址、现在的价格和对应的 tick。
铸造(Minting)
在 UniswapV2 中,提供流动性被称作 铸造(mint),
因为 UniswapV2 的池子给予 LP-token 作为提供流动性的交换。
V3 没有这种行为,但是仍然保留了同样的名字,我们在这里也同样使用这个名字:
function mint(
address owner,
int24 lowerTick,
int24 upperTick,
uint128 amount
) external returns (uint256 amount0, uint256 amount1) {
...
mint 函数会包含以下参数:
token所有者的地址,来识别是谁提供的流动性;- 上限和下限价格对应的
tick,来设置价格区间的边界; - 希望提供的流动性的数量
简单描述一下铸造函数如何工作:
- 用户指定价格区间和流动性的数量;
- 合约更新
ticks和positions的mapping; - 合约计算出用户需要提供的
token数量(在本节我们用事先计算好的值);
- 获取
slot0中当前的价格和tick index - 根据提供的
tick区间值计算价格区间 - 根据当前价格和上下限价格,计算流动性值,取最小值
- 根据最小流动性值计算需要的
Tokens数量
- 合约从用户处获得
tokens,并且验证数量是否正确。
首先来检查 ticks:
if (
lowerTick >= upperTick ||
lowerTick < MIN_TICK ||
upperTick > MAX_TICK
) revert InvalidTickRange();
并且确保流动性的数量不为零:
if (amount == 0) revert ZeroLiquidity();
接下来,增加 tick 和 position 的信息:
ticks.update(lowerTick, amount);
ticks.update(upperTick, amount);
Position.Info storage position = positions.get(
owner,
lowerTick,
upperTick
);
position.update(amount);
ticks.update 函数如下所示:
// src/lib/Tick.sol
function update(
mapping(int24 => Tick.Info) storage self,
int24 tick,
uint128 liquidityDelta
) internal {
Tick.Info storage tickInfo = self[tick];
uint128 liquidityBefore = tickInfo.liquidity;
uint128 liquidityAfter = liquidityBefore + liquidityDelta;
if (liquidityBefore == 0) {
tickInfo.initialized = true;
}
tickInfo.liquidity = liquidityAfter;
}
它初始化一个流动性为 0 的 tick,并且在上面添加新的流动性。
正如上面所示,我们会在下限 tick 和上限 tick 处均调用此函数,流动性在两边都有添加。
position.update 函数如下所示:
// src/libs/Position.sol
function update(Info storage self, uint128 liquidityDelta) internal {
uint128 liquidityBefore = self.liquidity;
uint128 liquidityAfter = liquidityBefore + liquidityDelta;
self.liquidity = liquidityAfter;
}
与 tick 的函数类似,它也在特定的位置上添加流动性。其中的 get 函数如下:
// src/libs/Position.sol
function get(
mapping(bytes32 => Info) storage self,
address owner,
int24 lowerTick,
int24 upperTick
) internal view returns (Position.Info storage position) {
position = self[
keccak256(abi.encodePacked(owner, lowerTick, upperTick))
];
}
...
每个位置都由三个变量所确定:拥有流动性的地址,下限 tick,上限 tick 。
我们将这三个变量哈希来减少数据存储开销:哈希结果只有 32 字节,而三个变量分别存储需要 96 字节。
让我们继续完成 mint 函数。接下来我们需要计算用户需要质押 token 的数量,幸运的是,我们在上一章中已经用公式计算出了对应的数值。在这里我们会在代码中硬编码这些数据:
amount0 = 0.998976618347425280 ether;
amount1 = 5000 ether;
在后面的章节中,我们会把这里替换成真正的计算。
现在,我们可以从用户处获得 token 了。这部分是通过 callback 来实现的:
uint256 balance0Before;
uint256 balance1Before;
if (amount0 > 0) balance0Before = balance0();
if (amount1 > 0) balance1Before = balance1();
IUniswapV3MintCallback(msg.sender).uniswapV3MintCallback(
amount0,
amount1
);
if (amount0 > 0 && balance0Before + amount0 > balance0())
revert InsufficientInputAmount();
if (amount1 > 0 && balance1Before + amount1 > balance1())
revert InsufficientInputAmount();
首先,我们记录下现在的 token 余额。接下来我们调用caller的 uniswapV3MintCallback 方法。
预期调用者为合约地址,因为普通用户地址无法实现 callback 函数。使用 callback 函数看起来很不用户友好,但是这能够让合约计算 token 的数量——这非常关键,因为我们无法信任用户。
调用者需要实现 uniswapV3MintCallback 来将 token 转给池子合约。
调用 callback 函数后,我们会检查池子合约的对应余额是否发生变化,并且增量应该大于 amount0 和 amount1:这意味着调用者已经把 token 转到了池子。
function uniswapV3MintCallback(
uint256 amount0,
uint256 amount1,
bytes calldata data
) public {
UniswapV3Pool.CallbackData memory extra = abi.decode(
data,
(UniswapV3Pool.CallbackData)
);
ERC20(extra.token0).transferFrom(extra.payer, msg.sender, amount0);
ERC20(extra.token1).transferFrom(extra.payer, msg.sender, amount1);
}
最后,发出一个 Mint 事件:
emit Mint(msg.sender, owner, lowerTick, upperTick, amount, amount0, amount1);
第一笔交易
计算交易数量
- 计算过程中的流动性保持不变
- 需要根据当前流动性值和当前价格,根据输入的 tokens 数量计算目标价格
- 根据目标价格和当前价格,计算另一种代币的输入/输出数量
- 执行 swap 后,更新当前池子的兑换价格和 tick 位置
首先,需要知道如何计算交易出入的数量。
同样,我们在这小节中也会硬编码我们希望交易的 USDC 数额,这里我们选择 42 USDC swap ETH。
在决定了我们希望投入的资金量之后,需要计算我们会获得多少 ETH token。
在 UniswapV2 中,我们会使用当前池子的资产数量来计算,
但是在 V3 中我们有 $L$ 和 $\sqrt{P}$,
并且我们知道在交易过程中,$L$ 保持不变而只有 $\sqrt{P}$ 发生变化
(当在同一区间内进行交易时,V3 的表现和 V2 一致)。我们还知道如下公式:
$$L = \frac{\Delta y}{\Delta \sqrt{P}}$$
并且,在这里我们知道了$\Delta y$。它正是我们希望投入的 42 USDC。
因此,我们可以根据公式得出投入的 42 USDC 会对价格造成多少影响:
$$\Delta \sqrt{P} = \frac{\Delta y}{L}$$
在 V3 中,我们得到了我们交易导致的价格变动(回忆一下,交易使得现价沿着曲线移动)。
知道了目标价格(target price),合约可以计算出投入 USDC 的数量和输出 ETH 的数量。
注意,$\sqrt{P}$ 用 Q64.96 定点数表示
我们将数字代入上述公式:
$$\Delta \sqrt{P} = \frac{42 \enspace USDC}{1517882343751509868544} * 2^{96} = 2192253463713690532467206957$$
把差价加到现在的 $\sqrt{P}$,我们就能得到目标价格:
USDC 兑换 ETH 会减少池子中 ETH 的数量,因此 ETH 的价格会上涨
$$\sqrt{P_{target}} - \sqrt{P_{current}} = \Delta \sqrt{P}$$
$$\sqrt{P_{target}} = \sqrt{P_{current}} + \Delta \sqrt{P}$$
$$\sqrt{P_{target}} = 5602277097478614198912276234240 + 2192253463713690532467206957 = 5604469350942327889444743441197$$
在 Python 中进行相应计算:
amount_in = 42 * eth price_diff = (amount_in * q96) // liq price_next = sqrtp_cur + price_diff print("New price:", (price_next / q96) ** 2) print("New sqrtP:", price_next) print("New tick:", price_to_tick((price_next / q96) ** 2)) # New price: 5003.913912782393 # New sqrtP: 5604469350942327889444743441197 # New tick: 85184
知道了目标价格,我们就能计算出投入 USDC 的数量和获得 ETH 的数量:
$$\Delta x = \Delta \frac{L}{\sqrt{p}} / 2^{96} = L * (\frac{1}{\sqrt{p_b}} - \frac{1}{\sqrt{p_c}}) / 2 ^{96} = \frac{L(\sqrt{p_b}-\sqrt{p_c})}{\sqrt{p_b}\sqrt{p_c}} / 2 ^ {96}$$ $$\Delta y = L(\sqrt{p_b}-\sqrt{p_c}) / 2 ^{96} $$
用Python:
amount_in = calc_amount1(liq, price_next, sqrtp_cur) amount_out = calc_amount0(liq, price_next, sqrtp_cur) print("USDC in:", amount_in / eth) print("ETH out:", amount_out / eth) # USDC in: 42.0 # ETH out: 0.008396714242162444
我们使用另一个公式验证一下:
$$\Delta x = \Delta \frac{1}{\sqrt{P}} L$$
使用上述公式,在知道价格变动和流动性数量的情况下,我们能求出我们购买了多少 ETH,也即 $\Delta x$。一个需要注意的点是: $\Delta \frac{1}{\sqrt{P}}$ 不等于 $\frac{1}{\Delta \sqrt{P}}$!前者才是 ETH 价格的变动,并且能够用如下公式计算:
$$\Delta \frac{1}{\sqrt{P}} = \frac{1}{\sqrt{P_{target}}} - \frac{1}{\sqrt{P_{current}}}$$
我们知道了公式里面的所有数值,接下来将其带入即可(可能会在显示上有些问题):
$$\Delta \frac{1}{\sqrt{P}} = \frac{1}{5604469350942327889444743441197} - \frac{1}{5602277097478614198912276234240}$$
$$\Delta \frac{1}{\sqrt{P}} = -0.00000553186106731426$$
接下来计算 $\Delta x$:
$$\Delta x = -0.00000553186106731426 * 1517882343751509868544 = -8396714242162698 $$
即 0.008396714242162698 ETH,这与我们第一次算出来的数量非常接近!注意到这个结果是负数,因为我们是从池子中提出 ETH。
实现swap
交易在 swap 函数中实现:
function swap(address recipient)
public
returns (int256 amount0, int256 amount1)
{
此时,它仅仅接受一个 recipient 参数,即提出 token 的接收者。
首先,我们需要计算出目标价格和对应 tick,以及 token 的数量。
同样,我们将会在这里硬编码我们之前计算出来的值:
int24 nextTick = 85184;
uint160 nextPrice = 5604469350942327889444743441197;
amount0 = -0.008396714242162444 ether;
amount1 = 42 ether;
接下来,我们需要更新现在的 tick 和对应的 sqrtP:
(slot0.tick, slot0.sqrtPriceX96) = (nextTick, nextPrice);
然后,manager 合约把对应的 token 发送给 recipient 并且让调用者将需要的 token 转移到本合约:
IERC20(token0).transfer(recipient, uint256(-amount0));
uint256 balance1Before = balance1();
IUniswapV3SwapCallback(msg.sender).uniswapV3SwapCallback(
amount0,
amount1
);
if (balance1Before + uint256(amount1) < balance1())
revert InsufficientInputAmount();
我们使用 callback 函数来将控制流转移到调用者,
让它转入 token,之后我们需要通过检查确认 caller 转入了正确的数额。
最后,合约释放出一个 swap 事件,使得该笔交易能够被监听到。这个事件包含了所有有关这笔交易的信息:
emit Swap(
msg.sender,
recipient,
amount0,
amount1,
slot0.sqrtPriceX96,
liquidity,
slot0.tick
);
本章中所有用到的 python 计算都在 unimath.py。
# Online Python compiler (interpreter) to run Python online.
# Write Python 3 code in this online editor and run it.
# Online Python compiler (interpreter) to run Python online.
# Write Python 3 code in this online editor and run it.
import math
min_tick = -887272
max_tick = 887272
q96 = 2**96
ETH = 10**18
def price_to_tick(p):
return math.floor(math.log(p, 1.0001))
def price_to_sqrtp(p):
return int(math.sqrt(p) * q96)
def sqrtp_to_price(sqrtp):
return (sqrtp / q96) ** 2
def tick_to_sqrtp(t):
return int((1.0001 ** (t / 2)) * q96)
def liquidity0(amount, pa, pb):
if pa > pb:
pa, pb = pb, pa
return (amount * (pa * pb) / q96) / (pb - pa)
def liquidity1(amount, pa, pb):
if pa > pb:
pa, pb = pb, pa
return amount * q96 / (pb - pa)
def calc_amount0(liq, pa, pb):
if pa > pb:
pa, pb = pb, pa
return int(liq * q96 * (pb - pa) / pb / pa)
def calc_amount1(liq, pa, pb):
if pa > pb:
pa, pb = pb, pa
return int(liq * (pb - pa) / q96)
# Liquidity provision
price_low = 0.7
price_cur = 1
price_upp = 1.2
sqrtp_low = price_to_sqrtp(price_low)
sqrtp_cur = price_to_sqrtp(price_cur)
sqrtp_upp = price_to_sqrtp(price_upp)
print(f"Price range: {sqrtp_low}-{sqrtp_upp}; current price: {sqrtp_cur}")
amount_ETH = 100 * ETH
amount_usdc = 100 * ETH
print(f"预计Deposit: {amount_ETH/ETH} ETH, {amount_usdc/ETH} USDC;")
liq = 0
if price_cur <= price_low:
liq = liquidity0(amount_ETH, sqrtp_cur, sqrtp_upp)
amount0 = calc_amount0(liq, sqrtp_upp, sqrtp_cur)
print(f"只收取Token0,实际Deposit: {amount0/ETH} ETH, liquidity: {liq}")
elif price_cur < price_upp:
liq0 = liquidity0(amount_ETH, sqrtp_cur, sqrtp_upp)
liq1 = liquidity1(amount_usdc, sqrtp_cur, sqrtp_low)
liq = int(min(liq0, liq1))
amount0 = calc_amount0(liq, sqrtp_upp, sqrtp_cur)
amount1 = calc_amount1(liq, sqrtp_low, sqrtp_cur)
print(f"实际Deposit: {amount0/ETH} ETH, {amount1/ETH} USDC; liquidity: {liq}")
amount_in = calc_amount1(liq, sqrtp_upp, sqrtp_cur)
print(f"买空ETH,USDC in:{amount_in / ETH}, USDC Left:{amount_in / ETH + amount1/ETH}")
amount_out = calc_amount0(liq, sqrtp_low, sqrtp_cur)
print(f"买空USDC,ETH In:{ amount_out / ETH},ETH Left:{ amount_out / ETH + amount0/ETH}",)
else :
liq = liquidity1(amount_usdc, sqrtp_cur, sqrtp_low)
amount1 = calc_amount1(liq, sqrtp_low, sqrtp_cur)
print(f"只收取Token1,实际Deposit: {amount1/ETH} USDC; liquidity: {liq}")
# Swap USDC for ETH
amount_in = 90 * ETH
print(f"\nSelling {amount_in/ETH} USDC")
price_diff = (amount_in * q96) // liq
price_next = sqrtp_cur + price_diff
print("New price:", (price_next / q96) ** 2)
print("New sqrtP:", price_next)
print("New tick:", price_to_tick((price_next / q96) ** 2))
amount_in = calc_amount1(liq, price_next, sqrtp_cur)
amount_out = calc_amount0(liq, price_next, sqrtp_cur)
print("USDC in:", amount_in / ETH)
print("ETH out:", amount_out / ETH)
# Swap ETH for USDC
amount_in = 85 * ETH
print(f"\nSelling {amount_in/ETH} ETH")
price_next = int((liq * q96 * sqrtp_cur) // (liq * q96 + amount_in * sqrtp_cur))
print("New price:", (price_next / q96) ** 2)
print("New sqrtP:", price_next)
print("New tick:", price_to_tick((price_next / q96) ** 2))
amount_in = calc_amount0(liq, price_next, sqrtp_cur)
amount_out = calc_amount1(liq, price_next, sqrtp_cur)
print("ETH in:", amount_in / ETH)
print("USDC out:", amount_out / ETH)
输出:
Price range: 66287036551430451535630303232-86790103597495583603102318592; current price: 79228162514264337593543950336
预计Deposit: 100.0 ETH, 100.0 USDC;
实际Deposit: 53.34216051094175 ETH, 100.0 USDC; liquidity: 612220008844691898368
买空ETH,USDC in:58.433409155808185, USDC Left:158.4334091558082
买空USDC,ETH In:119.52286093343936,ETH Left:172.8650214443811
Selling 90.0 USDC
New price: 1.3156227092534618
New sqrtP: 90875175880814835159951393049
New tick: 2743
USDC in: 90.0
ETH out: 78.46515351602369
Selling 85.0 ETH
New price: 0.7710372403582774
New sqrtP: 69569240325740947748657834520
New tick: -2601
ETH in: 85.0
USDC out: 74.63741730250688
Preference
https://www.rapidtables.com/calc/math/log-calculator.html
https://www.programiz.com/python-programming/online-compiler/
管理合约(Manager Contract)
在部署我们的池子合约之前,仍然有一个问题需要解决。我们之前提到过,UniswapV3 合约由两部分构成:
- 核心合约(
core contracts)实现了最核心的功能,不提供用户友好的交互接口 - 外围合约(
periphery contracts)为核心合约实现了用户友好的接口
池子合约是核心合约,它并不需要用户友好或者实现灵活功能。它需要调用者进行所有的计算并且提供合适的参数。同时,它也没有使用ERC20的 transferFrom 函数来从调用者处转账,而是使用了两个 callback 函数:
uniswapV3MintCallback,当铸造流动性的时候被调用,检查代币对的存款情况uniswapV3SwapCallback,当交易token的时候被调用,检查目标代币的存款情况
由于只有合约才能实现 callback 函数,池子合约并不能直接被普通用户(EOA)调用。
我们下一步的目标是将这个池子合约部署在一个本地的区块链上,并且使用一个前端应用与其交互。 因此我们需要创建一个合约,能够让非合约的地址也与池子进行交互。让我们来实现吧!
工作流程
下面我们描述了管理合约的功能:
- 为了铸造流动性,我们需要
approve对应的token给管理合约; - 我们会调用管理合约的
mint函数来铸造流动性,参数为铸造需要的参数以及池子的合约地址; - 管理合约会调用池子的
mint函数,并且会实现uniswapV3MintCallback。由于我们之前的approve,管理合约会从我们的账户中把token转到池子合约; - 为了交易
token,我们也需要approve对应的token; - 我们会调用管理合约的
swap函数,并且与mint过程类似,它会调用池子合约的对应函数。管理者合约会把我们的token转到池子中,池子进行对应的交易,然后把得到的token发回给我们。
综上,管理合约主要作为用户和池子之间的中介来运行。
向 callback 传递数据
在实现管理合约之前,我们还需要更新我们的池子合约。
管理者合约需要能够与任何一个流动性池适配,并且能够允许任何地址调用它。为了达到这一点,我们需要对 callback 进行升级:
我们需要将池子的地址和用户的地址作为参数传递。下面是我们对于 uniswapV3MintCallback 之前的实现(测试合约中的):
function uniswapV3MintCallback(uint256 amount0, uint256 amount1) public {
if (transferInMintCallback) {
token0.transfer(msg.sender, amount0);
token1.transfer(msg.sender, amount1);
}
}
关键点:
- 这个函数转移的
token是属于这个测试合约的——而我们希望使用transferFrom来从管理合约的调用者出转出token - 这个函数需要知道
token0和token1,但这两个变量会随着不同池子而变化。
想法:我们需要改变 callback 的参数,来将用户和池子的合约地址传进去。
接下来看一下 swap 的 callback:
function uniswapV3SwapCallback(int256 amount0, int256 amount1) public {
if (amount0 > 0 && transferInSwapCallback) {
token0.transfer(msg.sender, uint256(amount0));
}
if (amount1 > 0 && transferInSwapCallback) {
token1.transfer(msg.sender, uint256(amount1));
}
}
同样,它从测试合约处转钱,并且已知 token0 和 token1。
为了将这些参数传递给 callback,我们需要首先将它们传递给 mint 和 swap 函数
(因为 callback 函数是被这两个函数调用的)。
然而,由于这些额外的数据并不会被上述两个函数本身使用,
为了避免参数的混淆,我们会使用 abi.encode() 来编码这些参数。
定义一下这些额外数据的结构:
// src/UniswapV3Pool.sol
struct CallbackData {
address token0;
address token1;
address payer;
}
...
接下来把编码后的数据传入 callback:
function mint(
address owner,
int24 lowerTick,
int24 upperTick,
uint128 amount,
bytes calldata data // <--- New line
) external returns (uint256 amount0, uint256 amount1) {
IUniswapV3MintCallback(msg.sender).uniswapV3MintCallback(
amount0,
amount1,
data // <--- New line
);
...
}
function swap(address recipient, bytes calldata data) // <--- `data` added
public
returns (int256 amount0, int256 amount1)
{
IUniswapV3SwapCallback(msg.sender).uniswapV3SwapCallback(
amount0,
amount1,
data // <--- New line
);
...
}
现在,我们可以在测试合约的 callback 函数中解析对应的数据:
function uniswapV3MintCallback(
uint256 amount0,
uint256 amount1,
bytes calldata data
) public {
if (transferInMintCallback) {
UniswapV3Pool.CallbackData memory extra = abi.decode(
data,
(UniswapV3Pool.CallbackData)
);
IERC20(extra.token0).transferFrom(extra.payer, msg.sender, amount0);
IERC20(extra.token1).transferFrom(extra.payer, msg.sender, amount1);
}
}
Swap 代币
完整的合约代码
Mint-添加流动性
初始化 tick 与更新
在 mint 函数中,更新 TickInfo 这个 mapping 来存储 tick 中可用的流动性信息。
首先,我们需要更新 Tick.update 函数:
// src/lib/Tick.sol
function update(
mapping(int24 => Tick.Info) storage self,
int24 tick,
uint128 liquidityDelta
) internal returns (bool flipped) {
...
flipped = (liquidityAfter == 0) != (liquidityBefore == 0);
...
}
现在,它会返回一个 flipped flag,当流动性被添加到一个空的 tick 或整个 tick 的流动性被耗尽时为 true。
接下来,在 mint 函数中,我们更新 bitmap 索引:
// src/UniswapV3Pool.sol
...
bool flippedLower = ticks.update(lowerTick, amount);
bool flippedUpper = ticks.update(upperTick, amount);
if (flippedLower) {
tickBitmap.flipTick(lowerTick, 1);
}
if (flippedUpper) {
tickBitmap.flipTick(upperTick, 1);
}
...
再次说明,在 Milestone 4 之前,TickSpacing 参数的值会始终为1.
Token 数量计算
mint 函数中最大的变化就是 token 数量的计算。在 milestone 1 中,我们硬编码了这些值:
amount0 = 0.998976618347425280 ether;
amount1 = 5000 ether;
现在,我们将使用与 milestone 1 中相同的公式,在 Solidity 中计算它。回顾一下这些公式:
$$\Delta x = \frac{L(\sqrt{p(i_u)} - \sqrt{p(i_c)})}{\sqrt{p(i_u)}\sqrt{p(i_c)}}$$ $$\Delta y = L(\sqrt{p(i_c)} - \sqrt{p(i_l)})$$
$\Delta x$ 代表 token0 的数量, 即 token $x$。让我们在 Solidity 中进行实现:
// src/lib/Math.sol
function calcAmount0Delta(
uint160 sqrtPriceAX96,
uint160 sqrtPriceBX96,
uint128 liquidity
) internal pure returns (uint256 amount0) {
if (sqrtPriceAX96 > sqrtPriceBX96)
(sqrtPriceAX96, sqrtPriceBX96) = (sqrtPriceBX96, sqrtPriceAX96);
require(sqrtPriceAX96 > 0);
amount0 = divRoundingUp(
mulDivRoundingUp(
(uint256(liquidity) << FixedPoint96.RESOLUTION),
(sqrtPriceBX96 - sqrtPriceAX96),
sqrtPriceBX96
),
sqrtPriceAX96
);
}
这个函数的功能与 Python 脚本中的
calc_amount0一致。
第一步是将两个价格排序来保证减法时不会溢出。
接下来,我们将 liquidity 转换成 Q64.96 格式的数字,只需要乘以 2**96。
下一步,根据公式,我们将其乘以价格之差并除以两个价格(先除以大的,再除以小的)。
两个除法的顺序并不重要,但是我们的除法要分两步进行,因为分母的乘法可能会导致溢出。
我们使用了 mulDivRoundingUp 函数来在一步中进行乘除。这个函数是基于 PRBMath 库中的 mulDiv:
function mulDivRoundingUp(
uint256 a,
uint256 b,
uint256 denominator
) internal pure returns (uint256 result) {
result = PRBMath.mulDiv(a, b, denominator);
if (mulmod(a, b, denominator) > 0) {
require(result < type(uint256).max);
result++;
}
}
mulmod 是Solidity的一个函数,将两个数 a 和 b 相乘,乘积除以 denominator,返回余数。如果余数为正,我们将结果上取整。
接下来是 $\Delta y$:
function calcAmount1Delta(
uint160 sqrtPriceAX96,
uint160 sqrtPriceBX96,
uint128 liquidity
) internal pure returns (uint256 amount1) {
if (sqrtPriceAX96 > sqrtPriceBX96)
(sqrtPriceAX96, sqrtPriceBX96) = (sqrtPriceBX96, sqrtPriceAX96);
amount1 = mulDivRoundingUp(
liquidity,
(sqrtPriceBX96 - sqrtPriceAX96),
FixedPoint96.Q96
);
}
这个函数与 Python 脚本中的
calc_amount1一致。
同样我们使用 mulDivRoundingUp 来防止乘法过程中的溢出。
现在它们都完成了!我们现在可以使用这些函数来计算 token 数量了:
// src/UniswapV3Pool.sol
function mint(...) {
...
Slot0 memory slot0_ = slot0;
amount0 = Math.calcAmount0Delta(
slot0_.sqrtPriceX96,
TickMath.getSqrtRatioAtTick(upperTick),
amount
);
amount1 = Math.calcAmount1Delta(
slot0_.sqrtPriceX96,
TickMath.getSqrtRatioAtTick(lowerTick),
amount
);
...
}
输出金额计算
需要在 Solidity 中实现数学运算。
但是,由于 Solidity 仅支持整数除法,在 Solidity 中实现数学运算会比较困难。
将使用第三方库来完成这部分
Uniswap 数学公式中还缺最后一个组成部分:计算卖出 ETH (即 token $x$ )时获得的资产数量。在前一章中,我们有一个类似的公式计算购买 ETH(购买 token $x$)的场景:
$$\Delta \sqrt{P} = \frac{\Delta y}{L}$$
这个公式计算卖出 token $y$ 时的价格变化。我们把这个差价加到现价上面,来得到目标价格:
$$\sqrt{P_{target}} = \sqrt{P_{current}} + \Delta \sqrt{P}$$
现在,我们需要一个类似的公式来计算卖出 token $x$(在本案例中为 ETH)买入 token $y$(在本案例中为 USDC)时的目标价格(在本案例中为卖出 ETH)。
回忆一下,token $x$ 的变化可以用如下方式计算:
$$\Delta x = \Delta \frac{1}{\sqrt{P}}L$$
$$\Delta y = \Delta {\sqrt{P}} L$$
从上面公式,我们可以推导出目标价格:
$$\Delta x = (\frac{1}{\sqrt{P_{target}}} - \frac{1}{\sqrt{P_{current}}}) L$$ $$= \frac{L}{\sqrt{P_{target}}} - \frac{L}{\sqrt{P_{current}}}$$
$$\ \sqrt{P_{target}} = \frac{\sqrt{P}L}{\Delta x \sqrt{P} + L}$$
$$\ \sqrt{P_{target}} = \frac{\Delta y}{L } + \sqrt{P}$$
知道了目标价格,我们就能够用前一章类似的方式计算出输出的金额
更新一下对应的 Python 脚本
# Swap ETH for USDC
amount_in = 0.01337 * eth
print(f"\nSelling {amount_in/eth} ETH")
price_next = int((liq * q96 * sqrtp_cur) // (liq * q96 + amount_in * sqrtp_cur))
print("New price:", (price_next / q96) ** 2)
print("New sqrtP:", price_next)
print("New tick:", price_to_tick((price_next / q96) ** 2))
amount_in = calc_amount0(liq, price_next, sqrtp_cur)
amount_out = calc_amount1(liq, price_next, sqrtp_cur)
print("ETH in:", amount_in / eth)
print("USDC out:", amount_out / eth)
输出:
Selling 0.01337 ETH
New price: 4993.777388290041
New sqrtP: 5598789932670289186088059666432
New tick: 85163
ETH in: 0.013369999999998142
USDC out: 66.80838889019013
上述结果显示,在之前提供流动性的基础上,卖出 0.01337 ETH 可以获得 66.8 USDC。
Solidity中的数学运算
由于 Solidity 不支持浮点数,在其中的运算会有些复杂。Solidity
拥有整数(integer)和无符号整数(unsigned integer)类型,这并不足够让我们实现复杂的数学运算。
另一个困难之处在于 gas 消耗:
一个算法越复杂,它消耗的 gas 就越多。
因此,如果我们需要比较高级的数学运算(例如exp, ln, sqrt),我们会希望它们尽可能节省 gas。
还有一个很大的问题是溢出。当进行 uint256 类型的乘法时,有溢出的风险:结果的数据可能会超出 256 位。
上述这些困难让我们不得不选择使用那些实现了高级数学运算并进行了gas优化的第三方库。
重用数学库
在 UniswapV3 实现中,我们会使用两个第三方数学库:
- PRBMath,一个包含了复杂的定点数运算的库。我们会使用其中的
mulDiv函数来处理乘除法过程中可能的溢出 - TickMath,来自原始的 Uniswap V3 仓库。这个合约实现了两个函数,
getSqrtRatioAtTick和getTickAtSqrtRatio,功能是在 tick 和 $\sqrt{P}$ 之间相互转换。
我们先关注第二个库。在我们的合约中,我们需要将 tick 转换成对应的 $\sqrt{P}$,或者反过来。对应的公式为:
$$P(i) = 1.0001^i $$
$$i = log_{1.0001}P(i)$$
这些是非常复杂的数学运算(至少在 Solidity 中是这样)并且它们需要很高的精度,因为我们不希望取整的问题干扰我们的价格计算。为了能实现更高的精度和 gas 优化,我们需要采用特定的实现。
getSqrtRatioAtTick 和 getTickAtSqrtRatio 的代码:
其中有大量的 magic number(像 0xfffcb933bd6fad37aa2d162d1a594001)
Tick Bitmap Index
作为开始动态交易的第一步,根据交易输入的 tokens 数量计算新的价格,根据价格计算交换后的 tick index
function swap(address recipient, bytes calldata data)
public
returns (int256 amount0, int256 amount1)
{
int24 nextTick = 85184;
...
}
当流动性在不同的价格区间中时,我们很难简单地计算出目标 tick。
事实上,我们需要根据不同区间中的流动性来找到它。
因此,我们需要对于所有拥有流动性的 tick 建立一个索引,
之后使用这个索引来寻找 tick 直到“填满”当前交易所需的流动性。
Bitmap
Bitmap 是一个用压缩的方式提供数据索引的常用数据结构。
一个 bitmap 实际上就是一个 0 和 1 构成的数组,
其中的每一位的位置和元素内容都代表某种外部的信息。
每个元素可以被看做是一个 flag:当值为 0 的时候,flag 没有被设置;
当值为 1 的时候,flag 被设置。
例如,数组 111101001101001 就是数字 31337。
这个数字需要两个字节来存储(0x7a69),而这两字节能够存储 16 个 flag(1字节=8位)。
UniswapV3 使用这个技术来存储关于 tick 初始化的信息:
也即哪个 tick 拥有流动性。当 flag 设置为(1),对应的 tick 有流动性;
当 flag 设置为(0),对应的 tick 没有被初始化,即没有流动性。
TickBitmap 合约
在池子合约中,tick 索引存储为一个状态变量:
contract UniswapV3Pool {
using TickBitmap for mapping(int16 => uint256);
mapping(int16 => uint256) public tickBitmap;
...
}
这里的存储方式是一个 mapping,key 的类型是 int16,value 的类型是 uint256。

数组中每个元素都对应一个 tick。为了更好地在数组中寻址,我们把数组按照字的大小划分:每个子数组为 256 位。为了找到数组中某个 tick 的位置,我们使用如下函数:
Tick.Update
在 添加流动性的时候,需要更新 ticks 上的流动性。
- 如果在当前 ticks 上首次添加流动性,该 ticks index 从 0 置为 1
- 如果移除该位置的流动性,该 ticks index 从 1 置为 0
library Tick {
struct Info {
bool initialized;
uint128 liquidity;
}
function update(
mapping(int24 => Tick.Info) storage self,
int24 tick,
uint128 liquidityDelta
) internal returns (bool flipped) {
Tick.Info storage tickInfo = self[tick];
uint128 liquidityBefore = tickInfo.liquidity;
uint128 liquidityAfter = liquidityBefore + liquidityDelta;
flipped = (liquidityAfter == 0) != (liquidityBefore == 0);
翻转 Tick index 的值
flipTick 这是一个 internal 函数,用于翻转 tick 的状态。它接收:
- self: 一个映射,每个
int16(word位置)对应一个uint256(256 bit)。 - tick: 要操作的
tick值。 - tickSpacing:
tick的间距(确保tick是合法的间隔点)。
function position(int24 tick) private pure returns (int16 wordPos, uint8 bitPos) {
wordPos = int16(tick >> 8);
bitPos = uint8(uint24(tick % 256));
}
/// @notice Flips the initialized state for a given tick from false to true, or vice versa
/// @param self The mapping in which to flip the tick
/// @param tick The tick to flip
/// @param tickSpacing The spacing between usable ticks
function flipTick(
mapping(int16 => uint256) storage self,
int24 tick,
int24 tickSpacing
) internal {
require(tick % tickSpacing == 0); // ensure that the tick is spaced
(int16 wordPos, uint8 bitPos) = position(tick / tickSpacing);
uint256 mask = 1 << bitPos;
self[wordPos] ^= mask;
}
uint256 mask = 1 << bitPos;
构建一个掩码,只有第 bitPos 位是 1,例如 bitPos = 10,mask 就是:
000000…00010000000000 (第 10 位是 1)
self[wordPos] ^= mask;
这里是关键:
❗为什么用异或 ^=
这是为了“翻转”某一位:
-
如果原本这一位是 0(未激活),那么 0 ^ 1 = 1,变成激活;
-
如果原本这一位是 1(激活),那么 1 ^ 1 = 0,变成未激活。
即:异或操作相同为 0,不同为 1。
✅ 所以:
第一次调用:tick 被标记为激活。
第二次调用:tick 被取消激活。
可以重复切换状态。
可视化示意图(假设 wordPos = 0):
self[0] = 0x00000000 00000000 00000000 00000000 ...
↑
bitPos = 10
第一次调用: 原始为 0
self[0] ^= 0x00000000 00000000 00000000 00000400 (bit 10 = 1)
结果: bit 10 被置为 1
第二次调用:
再次异或: 1 ^ 1 = 0
bit 10 被清除
在Words中寻找Tick的方向
接下来是通过 bitmap 索引来寻找带有流动性的 tick。
在 swap 过程中,我们需要找到现在 tick 左边或者右边的下一个有流动性的 tick。
现在使用 bitmap 索引来找到这个值, 从下面单个方向展开:
tick寻找方向(左 or 右)bit的存储顺序(高位 or 低位)tick word的排列(内存结构)
🧠 基本术语
tick:价格单位刻度。
word:Uniswap 用一个 uint256 来存储 256 个 tick 是否被初始化(二进制位:0/1)。
wordPos:tick 所在的 word。
bitPos:tick 在该 word 内的位置(0~255)。
🔁 “方向是反的”的含义
✅ 目标行为(直接理解):
| 操作 | Tick 变化方向 | sqrtPriceX96 变化 | 价格 (Token1 per Token0) |
|---|---|---|---|
| 买入 Token0 (卖 Token1) | Tick ↑ 向右 | 上升 | 上升 |
| 卖出 Token0 (买 Token1) | Tick ↓ 向左 | 下降 | 下降 |
⚠️ 实际 bit 顺序问题:
在 Solidity 计算 tick_ bit_pos 的排列如下(Big-Endian)
uint256 bitmap: [bit255 bit254 ... bit1 bit0]
bitPos值: ↑ ↑ ↑ ↑
tick值: tick=511 tick=510 ... tick=256
← tick 增大方向 ←←←←←←←←←←←←←←←←←←←←←
也就是说:
| tick 越大 | 存在于 uint256 的越低位 | 实际取值的 bitPos 越小 |
|---|---|---|
| tick 越小 | 存在于 uint256 的越高位 | 实际取值的 bitPos 越大 |
这就导致:
| 操作行为 | 直接理解方向(tick) | 实际代码方向(bit) |
|---|---|---|
| 买入 token X | 价格上涨(tick变大) | 向左(bitPos减小),向bitPos-1、bitPos-2、…0搜索 |
| 卖出 token X | 价格下跌(tick变小) | 向右(bitPos增加),向 bitPos+1、bitPos+2、…255搜索 |
计算下一个有效的Tick Index
如果当前 word 内不存在有流动性的 tick,我们将会在下一个循环中,在相邻的 word 中继续寻找。
现在让我们来实现:
function nextInitializedTickWithinOneWord(
mapping(int16 => uint256) storage self,
int24 tick,
int24 tickSpacing,
bool lte
) internal view returns (int24 next, bool initialized) {
int24 compressed = tick / tickSpacing;
...
tick代表现在的tick;tickSpaceing在本章节中一直为 1;lte是一个设置方向的flag
- 为
true时,我们是卖出 token $x$,在右边寻找下一个 tick; - false 时相反。
if (lte) {
(int16 wordPos, uint8 bitPos) = position(compressed);
uint256 mask = (1 << bitPos) - 1 + (1 << bitPos);
uint256 masked = self[wordPos] & mask;
...
当卖出 token $x$ 时,我们需要:
- 获得现在
tick的对应位置 - 求出一个掩码,当前位及所有右边的位为 1
- 将掩码覆盖到当前
word上,得出右边的所有位
initialized = masked != 0;
next = initialized
? (compressed - int24(uint24(bitPos - BitMath.mostSignificantBit(masked)))) * tickSpacing
: (compressed - int24(uint24(bitPos))) * tickSpacing;
...
接下来,masked 不为 0 表示右边至少有一个 tick 对应的位为 1。如果有这样的 tick,那右边就有流动性;否则就没有(在当前 word 中)。根据结果,我们要么求出下一个有流动性的 tick 位置,或者下一个 word 的最左边一位——这让我们能够在下一个循环中搜索下一个 word 里面的有流动性的 tick。
...
} else {
(int16 wordPos, uint8 bitPos) = position(compressed + 1);
uint256 mask = ~((1 << bitPos) - 1);
uint256 masked = self[wordPos] & mask;
...
类似地,当卖出 $y$ 时:
- 获取下一个 tick 的位置;
- 求出一个不同的掩码,当前位置所有左边的位为 1;
- 应用这个掩码,获得左边的所有位。
同样,如果当前 word 左边没有有流动性的 tick,返回上一个 word 的最右边一位:
...
initialized = masked != 0;
// overflow/underflow is possible, but prevented externally by limiting both tickSpacing and tick
next = initialized
? (compressed + 1 + int24(uint24((BitMath.leastSignificantBit(masked) - bitPos)))) * tickSpacing
: (compressed + 1 + int24(uint24((type(uint8).max - bitPos)))) * tickSpacing;
}
这样就完成了!
正如你所见,nextInitializedTickWithinOneWord 并不一定真正找到了我们想要的 tick——它的搜索范围仅仅包括当前 word。事实上,我们并不希望在这个函数里循环遍历所有的 word,因为我们并没有传入边界的参数。这个函数会在 swap 中正确运行——我们马上就会看到。
通用 swap
一笔交易可以看作是满足一个订单:
一个用户提交了一个订单,需要从池子中购买一定数量的某种 token。
池子会使用可用的流动性来将投入的 token0 数量“转换”成输出的 token1 数量。
如果在当前价格区间中没有足够的流动性,它将会尝试在其他价格区间中寻找流动性。
现在,我们要实现 swap 函数内部的逻辑,
但仍然保证交易可以在当前价格区间内完成——跨 tick 的交易将会在下一个 milestone 中实现。
function swap(
address recipient,
bool zeroForOne,
uint256 amountSpecified,
bytes calldata data
) public returns (int256 amount0, int256 amount1) {
...
在 swap 函数中,我们新增了两个参数:zeroForOne 和 amountSpecified。
zeroForOne 是用来控制交易方向的 flag:
true,表示卖出Token0, 用token0兑换token1;false则相反。
amountSpecified 是用户希望兑换到的 token 数量。
完成兑换订单
由于在 UniswapV3 中,流动性存储在不同的价格区间中,池子合约需要找到“填满当前订单”所需要的所有流动性。
这个操作是通过沿着某个方向遍历所有初始化的 tick 来实现的。
在继续之前,我们需要定义两个新的结构体:
struct SwapState {
uint256 amountSpecifiedRemaining;
uint256 amountCalculated;
uint160 sqrtPriceX96;
int24 tick;
}
struct StepState {
uint160 sqrtPriceStartX96;
int24 nextTick;
uint160 sqrtPriceNextX96;
uint256 amountIn;
uint256 amountOut;
}
SwapState 维护了当前 swap 的状态。
amoutSpecifiedRemaining跟踪了还需要从池子中获取的token数量:当这个数量为 0 时,这笔订单就被填满了。amountCalculated是由合约计算出的输出数量。sqrtPriceX96和tick是交易结束后的价格和tick。
StepState 维护了当前交易“一步”的状态。这个结构体跟踪“填满订单”过程中一个循环的状态。
sqrtPriceStartX96跟踪循环开始时的价格。nextTick是能够为交易提供流动性的下一个已初始化的tick,sqrtPriceNextX96是下一个tick的价格。amountIn和amountOut是当前循环中流动性能够提供的数量。
在我们实现跨 tick 的交易后(也即不发生在一个价格区间中的交易),关于循环方面会有更清晰的了解。
Slot0 memory slot0_ = slot0;
SwapState memory state = SwapState({
amountSpecifiedRemaining: amountSpecified,
amountCalculated: 0,
sqrtPriceX96: slot0_.sqrtPriceX96,
tick: slot0_.tick
});
在填满一个订单之前,我们首先获取当前池子中的价格和tick Index, 然后初始化 SwapState 的实例。
我们将会循环直到 amoutSpecified == 0,也即池子拥有足够的流动性来买用户的 amountSpecified 数量的token。
while (state.amountSpecifiedRemaining > 0) {
.....
}
计算兑换的价格区间
初始化 step 变量
在循环中,每次初始化新的 step 变量
sqrtPriceStartX96- 第一次循环的值为当前池子内部的价格
- 之后的每次循环,该值都是执行完当前一定数量代币
swap后的价格
nextTick- 根据循环外的
state变量记录的Tick_Index和方向寻找到的下一个有流动性代币的Tick_Index
- 根据循环外的
sqrtPriceNextX96nextTick对应的价格
amountIn,amountOut- 按照 当前的流动性 和
sqrtPriceStartX96 ~ sqrtPriceNextX96价格区间,计算得出的最大可 swap 的代币数量- 大于等于当前需要的代币数量的话,按照实际兑换数量计算新的价格
- 小于的话,在当前区间内执行部分兑换并更新
tick = nextTick,sqrtPriceStartX96 = sqrtPriceNextX96,进入下一个循环
- 按照 当前的流动性 和
while (state.amountSpecifiedRemaining > 0) {
StepState memory step;
step.sqrtPriceStartX96 = state.sqrtPriceX96;
(step.nextTick, ) = tickBitmap.nextInitializedTickWithinOneWord(
state.tick,
1,
zeroForOne
);
step.sqrtPriceNextX96 = TickMath.getSqrtRatioAtTick(step.nextTick);
(state.sqrtPriceX96, step.amountIn, step.amountOut) = SwapMath
.computeSwapStep(
step.sqrtPriceStartX96,
step.sqrtPriceNextX96,
liquidity,
state.amountSpecifiedRemaining
);
SwapMath.computeSwapStep 合约
本章介绍的是在同一个价格区间内可以完成的兑换,不考虑进入下次循环。
首先根据输入的代币数量和当前池子的价格计算出兑换后的最新价格: 计算公式:
$$\sqrt{P_{target}} = \frac{\sqrt{P}L}{\Delta x \sqrt{P} + L}$$
当它可能产生溢出时,我们使用另一个替代的公式,精确度会更低但是不会溢出:
$$\sqrt{P_{target}} = \frac{L}{\Delta x + \frac{L}{\sqrt{P}}}$$
$$\ \sqrt{P_{target}} = \frac{\Delta y}{L } + \sqrt{P}$$
function computeSwapStep(
uint160 sqrtPriceCurrentX96,
uint160 sqrtPriceTargetX96,
uint128 liquidity,
uint256 amountRemaining
)
internal
pure
returns (
uint160 sqrtPriceNextX96,
uint256 amountIn,
uint256 amountOut
)
{
bool zeroForOne = sqrtPriceCurrentX96 >= sqrtPriceTargetX96;
sqrtPriceNextX96 = Math.getNextSqrtPriceFromInput(
sqrtPriceCurrentX96,
liquidity,
amountRemaining,
zeroForOne
);
根据 sqrtPriceCurrentX96 ~ sqrtPriceNextX96 计算代币对的预期输入和输出数量
计算公式:
$$\Delta x = \Delta \frac{1}{\sqrt{P}}L$$
$$\Delta y = \Delta {\sqrt{P}} L$$
amountIn = Math.calcAmount0Delta(
sqrtPriceCurrentX96,
sqrtPriceNextX96,
liquidity
);
amountOut = Math.calcAmount1Delta(
sqrtPriceCurrentX96,
sqrtPriceNextX96,
liquidity
);
更新 state变量
if (state.tick != slot0_.tick) {
(slot0.sqrtPriceX96, slot0.tick) = (state.sqrtPriceX96, state.tick);
}
(amount0, amount1) = zeroForOne
? (
int256(amountSpecified - state.amountSpecifiedRemaining),
-int256(state.amountCalculated)
)
: (
-int256(state.amountCalculated),
int256(amountSpecified - state.amountSpecifiedRemaining)
);
执行兑换
到目前为止,已经能够沿着下一个初始化过的tick进行循环;
填满用户指定的 amoutSpecified、计算输入和输出数量,
并且找到新的价格和 tick。
根据交易方向与用户交换 token
- 先将一定数量的目标代币转到接收地址
- 收取一定数量的输入代币,通过
IUniswapV3SwapCallback实现
if (zeroForOne) {
ERC20(token1).transfer(recipient, uint256(-amount1));
uint256 balance0Before = balance0();
IUniswapV3SwapCallback(msg.sender).uniswapV3SwapCallback(
amount0,
amount1,
data
);
if (balance0Before + uint256(amount0) > balance0())
revert InsufficientInputAmount();
} else {
ERC20(token0).transfer(recipient, uint256(-amount0));
uint256 balance1Before = balance1();
IUniswapV3SwapCallback(msg.sender).uniswapV3SwapCallback(
amount0,
amount1,
data
);
if (balance1Before + uint256(amount1) > balance1())
revert InsufficientInputAmount();
}
报价合约
用户会输入希望卖出的 tokena 数量,
然后就能计算并且展示出它们会获得的 tokenb 数量。
由于 UniswapV3 中的流动性是分散在多个价格区间中的,我们不能够仅仅通过一个公式计算出对应数量.
UniswapV3 的设计需要我们用一种不同的方法:
为了获得交易数量,我们初始化一个真正的交易,
并且在 callback 函数中打断它,获取到之前计算出的对应数量。
也就是,我们将会模拟一笔真实的交易来计算输出数量!
contract UniswapV3Quoter {
struct QuoteParams {
address pool;
uint256 amountIn;
bool zeroForOne;
}
function quote(QuoteParams memory params)
public
returns (
uint256 amountOut,
uint160 sqrtPriceX96After,
int24 tickAfter
)
{
...
Quoter 合约仅实现了一个 public 的函数 quote。
Quoter是一个对于所有池子的通用合约,
因此它将池子地址作为一个参数。其他参数(amountIn 和 zeroForOne)都是模拟 swap 需要的参数。
try
IUniswapV3Pool(params.pool).swap(
address(this),
params.zeroForOne,
params.amountIn,
abi.encode(params.pool)
)
{} catch (bytes memory reason) {
return abi.decode(reason, (uint256, uint160, int24));
}
这个函数唯一实现的功能是调用池子合约的 swap 函数。
这个调用应当 revert
function uniswapV3SwapCallback(
int256 amount0Delta,
int256 amount1Delta,
bytes memory data
) external view {
address pool = abi.decode(data, (address));
uint256 amountOut = amount0Delta > 0
? uint256(-amount1Delta)
: uint256(-amount0Delta);
(uint160 sqrtPriceX96After, int24 tickAfter) = IUniswapV3Pool(pool)
.slot0();
在 swap 的 callback 中,我们收集我们想要的值:输出数量、新的价格以及对应的 tick。
接下来,我们将会把这些值保存下来并且 revert:
assembly {
let ptr := mload(0x40)
mstore(ptr, amountOut)
mstore(add(ptr, 0x20), sqrtPriceX96After)
mstore(add(ptr, 0x40), tickAfter)
revert(ptr, 96)
}
为了节约 gas,这部分使用 Yul 来实现,这是一个在 Solidity 中写内联汇编的语言。
mload(0x40)读取下一个可用 memory slot 的指针(EVM 中的 memory 组织成 32 字节的 slot 形式);- 在这个 memory slot,
mstore(ptr, amountOut)写入amountOut。 mstore(add(ptr, 0x20), sqrtPriceX96After)在amountOut后面写入sqrtPriceX96After。mstore(add(ptr, 0x40), tickAfter)在sqrtPriceX96After后面写入tickAfter。revert(ptr, 96)会 revert 这个调用,并且返回 ptr 指向位置的 96 字节数据。
所以,我们实际上就是把我们需要的值的字节表示连接起来(也就是 abi.encode() 做的事)。
注意到偏移永远是 32 字节,即使 sqrtPriceX96After 大小只有 20 字节(uint160),
tickAfter 大小只有 3 字节(uint24)。
这也是为什么我们能够使用 abi.decode() 来解码数据:
因为 abi.encode() 就是把所有的数编码成 32 字节。
回顾
我们来回顾一下以便于更好地理解这个算法:
quote调用一个池子的swap函数,参数是输入的 token 数量和交易方向。swap进行一个真正的交易,运行一个循环来填满用户需要的数量。- 为了从用户那里获得 token,
swap会调用 caller 的 callback 函数。 - 调用者(报价合约)实现了 callback,在其中它 revert 并且附带了输出数量、新的价格、新的 tick 这些信息。
- revert 一直向上传播到最初的
quote调用 - 在
quote中,这个 revert 被捕获,reason 被解码并作为了quote调用的返回值。
希望上面的解释能让你对这个流程更加清晰!
Quoter 的限制
这样的设计有一个非常明显的限制之处:
由于 quote 调用了池子合约的 swap 函数,
而 swap 函数既不是 pure 的也不是 view 的(因为它修改了合约状态);
quoter 也同样不能成为一个 pure 或者 view 的函数,即使它永远都不会修改合约的状态。
跨tick交易
在这个milestone中,会:
- 更新
mint函数,使得能够在不同的价格区间提供流动性; - 更新
swap函数,使得在当前价格区间流动性不足时能够跨价格区间交易; - 学习如何在智能合约中计算流动性;
- 在
mint和swap函数中实现滑点控制; - 增加对于定点数运算的一些了解。
完整合约代码
不同价格区间
在之前的实现中,仅仅创建包含现价的价格区间:
// src/UniswapV3Pool.sol
function mint(
...
amount0 = Math.calcAmount0Delta(
slot0_.sqrtPriceX96,
TickMath.getSqrtRatioAtTick(upperTick),
amount
);
amount1 = Math.calcAmount1Delta(
slot0_.sqrtPriceX96,
TickMath.getSqrtRatioAtTick(lowerTick),
amount
);
liquidity += uint128(amount);
...
}
从这段代码中也可以看到,总是会更新流动性 liquidity(跟踪现在可用的流动性,即在现价时候可用的流动性)。
然而,也可以创建低于或高于现价的价格区间。
UniswapV3 的设计允许 LP 提供当前不可用的流动性。
这些流动性只有当现价进入这些“休眠”的流动性区间时才会被“激活”。
以下是几种可能存在的价格区间情况:
- 活跃价格区间,也即包含现价的价格区间;
- 低于现价的价格区间,该价格区间的上界
upper_tick低于现价tick; - 高于现价的价格区间,该价格区间的下界
lower_tick高于现价tick。
限价单
一个有趣的事实是:非活跃的流动性(所在区间不包含现价)可以被看做是限价单(limit orders)。
在交易中,限价单是一种当价格突破用户设定的某个点的时候才会被执行的订单。
例如,你希望开一个限价单,当 ETH 价格低于 $1000 的时候买入一个 ETH。
在 UniswapV3 中,你可以通过在非活跃价格区间提供流动性来达到类似的目的。
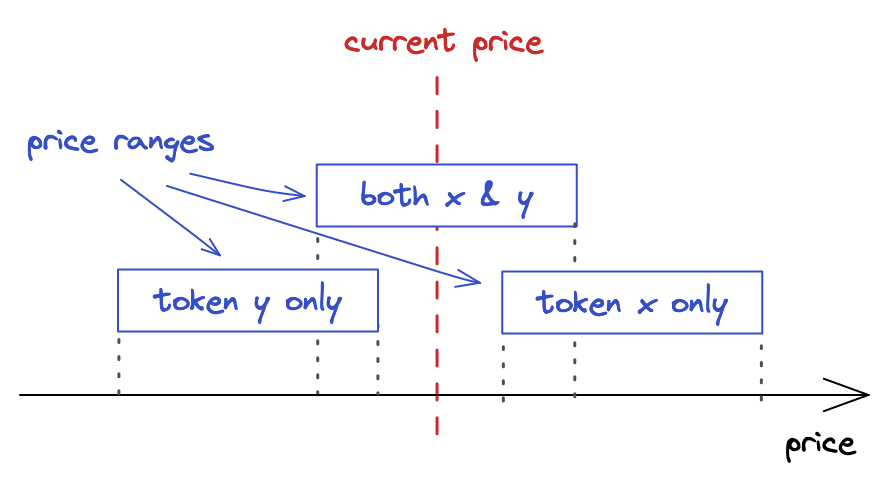
如果在低于或高于现价的位置提供流动性(整个价格区间都低于/高于现价),
那么你提供的流动性将完全由一种资产组成(因此跨 Tick 区间交易的时候,只会想要兑换一种 Token)。
在我们的例子中,我们的池子是把 ETH 作为 token $x$,把 USDC 作为 token $y$ ,我们的价格定义为:
$$P = \frac{y}{x}$$
如果我们把流动性放置在低于现价的区间,那么流动性将只会由 USDC 组成,因为当我们添加流动性的时候 USDC 的价格低于现价。
类似地,如果我们高于现价的区间提供流动性,那么流动性将完全由 ETH 组成,因为 ETH 的价格低于现价。
回顾一下我们在简介中的图表:

- 如果我们购买这个区间中所有可用的
ETH,这个区间内将只会由另一种token组成:- 上个区间的 ETH 不够兑换的话,会进入当前区间的右边继续兑换
ETH,也就是右边的区间需要为接下来的交易提供ETH- 如果我们持续购买并且拉高价格,可能会继续“耗尽”下一个价格区间,也即买走它所有的
ETH
- 如果我们持续购买并且拉高价格,可能会继续“耗尽”下一个价格区间,也即买走它所有的
- 上个区间的 ETH 不够兑换的话,会进入当前区间的右边继续兑换
- 类似地,如果我们购买
USDC,我们会使得价格下跌,价格曲线向左移动并且从池子中移出USDC- 下一个价格区间会仅包含
USDC代币来满足需求- 并且类似地,如果我们继续买光这个区间的所有
USDC,它也会以仅包含ETH而中止
- 并且类似地,如果我们继续买光这个区间的所有
- 下一个价格区间会仅包含
注意到一个有趣的点:当跨越整个价格区间时,其中的流动性从一种 token 交易为另外一种。
并且如果我们设置一个相当窄的价格区间,价格会快速越过整个区间,我们就得到了一个限价单!
例如,如果我们想在某个低价点购入 ETH,我们可以在一个低价区间提供仅包含 USDC 的流动性,等待价格越过这个区间。
在这之后,我们就可以移出流动性,所有的 USDC 都转换成了 ETH!
更新 mint 函数
为了支持上面提到的各种价格区间,我们需要知道现价究竟是低于、位于、高于用户提供的价格区间,
并且计算相应的 token 数量。
- 如果价格区间高于现价,我们希望它的流动性仅仅由 token $x$ 组成
- 如果价格区间低于现价,我们希望它的流动性仅仅由 token $y$ 组成
- 现价处于当前价格区间,则计算两种代币的数量并且更新当前的流动性
if (slot0_.tick < lowerTick) {
amount0 = Math.calcAmount0Delta(
TickMath.getSqrtRatioAtTick(lowerTick),
TickMath.getSqrtRatioAtTick(upperTick),
amount
);
} else if (slot0_.tick < upperTick) {
amount0 = Math.calcAmount0Delta(
slot0_.sqrtPriceX96,
TickMath.getSqrtRatioAtTick(upperTick),
amount
);
amount1 = Math.calcAmount1Delta(
slot0_.sqrtPriceX96,
TickMath.getSqrtRatioAtTick(lowerTick),
amount
);
liquidity = LiquidityMath.addLiquidity(liquidity, int128(amount)); // TODO: amount is negative when removing liquidity
} else {
amount1 = Math.calcAmount1Delta(
TickMath.getSqrtRatioAtTick(lowerTick),
TickMath.getSqrtRatioAtTick(upperTick),
amount
);
}
流动性计算
在 UniswapV3 的所有数学公式中,只剩流动性计算我们还没在 Solidity 里面实现。
def liquidity0(amount, pa, pb):
if pa > pb:
pa, pb = pb, pa
return (amount * (pa * pb) / q96) / (pb - pa)
def liquidity1(amount, pa, pb):
if pa > pb:
pa, pb = pb, pa
return amount * q96 / (pb - pa)
实现 Token X 的流动性计算
要实现的函数是在已知 token 数量和价格区间的情况下计算流动性($L = \sqrt{xy}$)。
$$\Delta x = (\frac{1}{\sqrt{P_{target}}} - \frac{1}{\sqrt{P_{current}}}) L$$ $$= \frac{L}{\sqrt{P_{target}}} - \frac{L}{\sqrt{P_{current}}}$$
简化之后: $$L = \frac{\Delta x \sqrt{P_u} \sqrt{P_l}}{\sqrt{P_u} - \sqrt{P_l}}$$
在 Solidity 中,我们仍然使用 PRBMath 来处理乘除过程中可能出现的溢出:
function getLiquidityForAmount0(
uint160 sqrtPriceAX96,
uint160 sqrtPriceBX96,
uint256 amount0
) internal pure returns (uint128 liquidity) {
if (sqrtPriceAX96 > sqrtPriceBX96)
(sqrtPriceAX96, sqrtPriceBX96) = (sqrtPriceBX96, sqrtPriceAX96);
uint256 intermediate = PRBMath.mulDiv(
sqrtPriceAX96,
sqrtPriceBX96,
FixedPoint96.Q96
);
liquidity = uint128(
PRBMath.mulDiv(amount0, intermediate, sqrtPriceBX96 - sqrtPriceAX96)
);
}
实现 Token Y 的流动性计算
类似得,我们将使用计算流动性中出现的另一个公式来在给定 $y$ 的数量和价格区间的前提下计算流动性:
$$\Delta y = \Delta\sqrt{P} L$$ $$L = \frac{\Delta y}{\sqrt{P_u}-\sqrt{P_l}}$$
function getLiquidityForAmount1(
uint160 sqrtPriceAX96,
uint160 sqrtPriceBX96,
uint256 amount1
) internal pure returns (uint128 liquidity) {
if (sqrtPriceAX96 > sqrtPriceBX96)
(sqrtPriceAX96, sqrtPriceBX96) = (sqrtPriceBX96, sqrtPriceAX96);
liquidity = uint128(
PRBMath.mulDiv(
amount1,
FixedPoint96.Q96,
sqrtPriceBX96 - sqrtPriceAX96
)
);
}
公平的流动性计算
在计算流动性时有如下逻辑:
- 如果我们在一个低于现价的价格区间计算流动性,我们使用 $\Delta y$ 版本的公式;
- 如果我们在一个高于现价的价格区间计算流动性,我们使用 $\Delta x$ 版本的公式;
- 如果现价在价格区间内,我们两个都计算并且挑选较小的一个。
function getLiquidityForAmounts(
uint160 sqrtPriceX96,
uint160 sqrtPriceAX96,
uint160 sqrtPriceBX96,
uint256 amount0,
uint256 amount1
) internal pure returns (uint128 liquidity) {
if (sqrtPriceAX96 > sqrtPriceBX96)
(sqrtPriceAX96, sqrtPriceBX96) = (sqrtPriceBX96, sqrtPriceAX96);
if (sqrtPriceX96 <= sqrtPriceAX96) {
liquidity = getLiquidityForAmount0(
sqrtPriceAX96,
sqrtPriceBX96,
amount0
);
} else if (sqrtPriceX96 <= sqrtPriceBX96) {
uint128 liquidity0 = getLiquidityForAmount0(
sqrtPriceX96,
sqrtPriceBX96,
amount0
);
uint128 liquidity1 = getLiquidityForAmount1(
sqrtPriceAX96,
sqrtPriceX96,
amount1
);
liquidity = liquidity0 < liquidity1 ? liquidity0 : liquidity1;
} else {
liquidity = getLiquidityForAmount1(
sqrtPriceAX96,
sqrtPriceBX96,
amount1
);
}
}
添加流动性中的滑点保护
添加流动性同样也需要滑点保护, 然而与 swap 函数不同的是,我们并不需要在池子合约中实现 mint 的滑点保护, 添加流动性的滑点保护是在管理合约中实现的。
管理合约是一个对于核心功能进行包装的合约,使得对于池子合约的调用更加便利。
为了在 mint 函数中实现滑点保护,
我们仅需要比较池子实际放入的 token 数量与用户选择的最低数量即可。
另外,我们也可以免除用户对于 $\sqrt{P_{lower}}$ 和 $\sqrt{P_{upper}}$ 的计算,在 Manager.mint() 中计算它们。
更新后的 mint 函数参数更多,我们包装在一个结构体中:
// src/UniswapV3Manager.sol
contract UniswapV3Manager {
struct MintParams {
address poolAddress;
int24 lowerTick;
int24 upperTick;
uint256 amount0Desired;
uint256 amount1Desired;
uint256 amount0Min;
uint256 amount1Min;
}
function mint(MintParams calldata params)
public
returns (uint256 amount0, uint256 amount1)
{
...
amount0Min 和 amount1Min 是通过滑点计算出的边界值。
它们必须比 desired 值小,其中的差值即为滑点。
LP 希望提供的 token 数量不少于 amount0Min 和 amount1Min。
接下来,我们计算 $\sqrt{P_{lower}}$,$\sqrt{P_{upper}}$ 和流动性:
function mint(MintParams calldata params)
public
returns (uint256 amount0, uint256 amount1)
{
IUniswapV3Pool pool = IUniswapV3Pool(params.poolAddress);
(uint160 sqrtPriceX96, ) = pool.slot0();
uint160 sqrtPriceLowerX96 = TickMath.getSqrtRatioAtTick(
params.lowerTick
);
uint160 sqrtPriceUpperX96 = TickMath.getSqrtRatioAtTick(
params.upperTick
);
uint128 liquidity = LiquidityMath.getLiquidityForAmounts(
sqrtPriceX96,
sqrtPriceLowerX96,
sqrtPriceUpperX96,
params.amount0Desired,
params.amount1Desired
);
(amount0, amount1) = pool.mint(
msg.sender,
params.lowerTick,
params.upperTick,
liquidity,
abi.encode(
IUniswapV3Pool.CallbackData({
token0: pool.token0(),
token1: pool.token1(),
payer: msg.sender
})
)
);
if (amount0 < params.amount0Min || amount1 < params.amount1Min)
revert SlippageCheckFailed(amount0, amount1);
}
跨 tick 交易
跨 tick 交易如何工作
一个通常的 UniswapV3 池子是一个有很多互相重叠的价格区间的池子。每个池子都会跟踪当前的价格 $\sqrt{P}$ 和 tick。
当用户交易 token,他们会使得现价和 tick 向左或向右移动,移动方向取决于当前的交易方向。
这样的移动是由于交易过程中某种 token 被添加进池子或者从池子中移除。
池子同样也会跟踪 $L$(代码中的 liquidity 变量),即所有包含现价的价格区间提供的总流动性。
通常来说,如果价格移动幅度较大,现价会移出一些价格区间之外。
这些时候,这种价格区间就会变为休眠,并且它们的流动性被从 $L$ 中减去。
另一方面,如果现价进入了某个价格区间,这个价格区间就会被激活并且 $L$ 会增加。
让我们来分析这样一个场景:
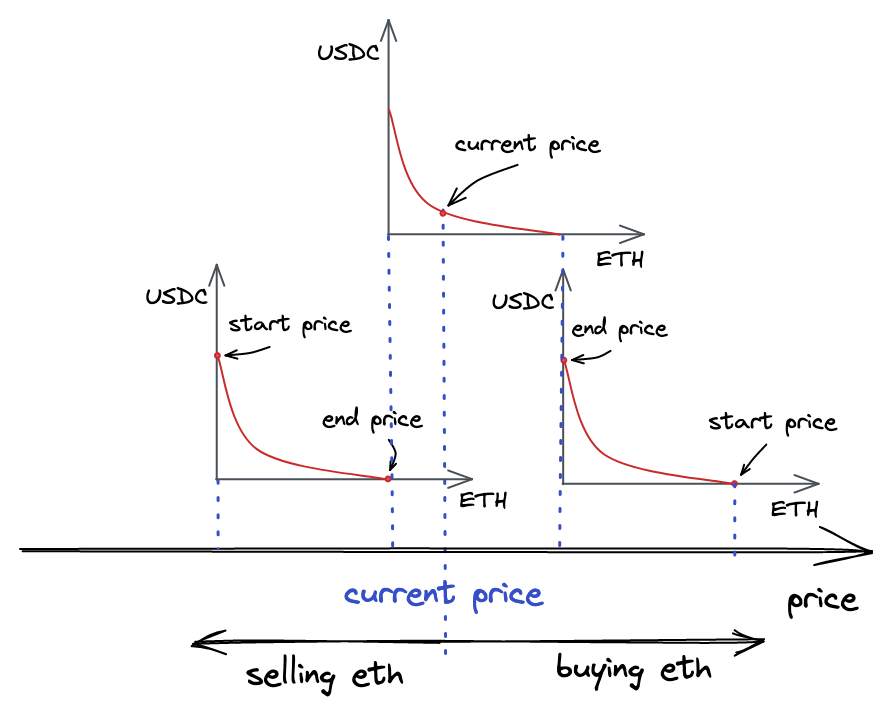
在图中有三个价格区间。最上面的一个是现在参与交易的区间,因为它包含现价。这个价格区间的流动性存储在池子合约中的 liquidity 变量中。
如果我们买走了最上面价格区间中的所有 ETH:
- 价格会升高并且我们会移动到右侧的价格区间中
- 右侧这个区间此时只往外兑
ETH- 如果现在流动性已经足够满足我们的交易需求
- 停留在这个价格区间中
liquidity变量仅包含当前价格区间的所有流动性
- 如果持续购买
ETH并且耗尽右边价格区间中的流动性- 需要跳到此价格区间右侧的另一个价格区间
- 如果那里没有其他价格区间了,就不得不停下来,这笔交易将仅会部分成交
- 如果现在流动性已经足够满足我们的交易需求
如果我们从最上面的价格区间中买走所有的 USDC:
- 价格会下降并且我们会移动到左边的价格区间中
- 左侧区间此时仅包含
USDC- 如果我们耗尽这个区间,就还需要再往左边的一个区间
现价会在交易过程中移动。它从一个价格区间移动到另一个价格区间,但是它一定会在某个价格区间之内——否则,就没有流动性可以交易。
当然,价格区间之间是可以重叠的
在价格区间重叠的部分,价格会移动得更缓慢。这是因为在这样的区域中供给量更高,所以需求的影响就会降低。
所以在实际中,直接在两个价格区间之间转移不太可能发生。
更新 SwapMath.computeSwapStep 函数
在 swap 函数中,我们会沿着已初始化的 tick(有流动性的 tick)循环,直到用户需求的数量被满足。
在每次循环中,我们会:
- 使用
tickBitmap.nextInitializedTickWithinOneWord来找到下一个已初始化的tick; - 在现价和下一个已初始化的
tick之间进行交易(使用SwapMath.computeSwapStep); - 总是假设当前流动性足够满足这笔交易(也即交易后的价格总在现价与下一个
tick对应的价格之间)
计算当前的价格区间内能够兑换的最大tokens数量
bool zeroForOne = sqrtPriceCurrentX96 >= sqrtPriceTargetX96;
amountIn = zeroForOne
? Math.calcAmount0Delta(
sqrtPriceCurrentX96,
sqrtPriceTargetX96,
liquidity
)
: Math.calcAmount1Delta(
sqrtPriceCurrentX96,
sqrtPriceTargetX96,
liquidity
);
需要考虑以下几个场景:
- 当现价和下一个 tick 之间的流动性足够填满
amoutRemaining- 当前
swap交易可以在当前的价格区间内被完成, 根据兑换数量和当前价格计算目标价格
- 当前
- 当这个区间不能填满
amoutRemaining- 当前价格区间无法完成完整的
swap交易- 将价格区间当道最大,完成当前区间的最大限度的兑换,会消耗掉当前区间所有流动性
- 剩余代币移动到下一个区间进行兑换
- 当前价格区间无法完成完整的
首先,计算
amountIn——当前区间可以满足的输入数量如果它比
amountRemaining要小,现在的区间不能满足整个交易,因此下一个 $\sqrt{P}$ 就会是当前区间的上界/下界(换句话说,我们使用了整个区间的流动性)。如果
amountIn大于amountRemaining,我们计算sqrtPriceNextX96——一个仍然在现在区间内的价格。最后,在找到下一个价格之后,我们在这个区间中重新计算
amountIn并计算amountOut。
// src/lib/SwapMath.sol
function computeSwapStep(...) {
if (amountRemaining >= amountIn) sqrtPriceNextX96 = sqrtPriceTargetX96;
else
sqrtPriceNextX96 = Math.getNextSqrtPriceFromInput(
sqrtPriceCurrentX96,
liquidity,
amountRemaining,
zeroForOne
);
amountIn = Math.calcAmount0Delta(
sqrtPriceCurrentX96,
sqrtPriceNextX96,
liquidity
);
amountOut = Math.calcAmount1Delta(
sqrtPriceCurrentX96,
sqrtPriceNextX96,
liquidity
);
}
更新 swap 函数
第二个分支是处理了交易仍然停留在当前区间的情况
else if (state.sqrtPriceX96 != step.sqrtPriceStartX96) {
state.tick = TickMath.getTickAtSqrtRatio(state.sqrtPriceX96);
}
现在,在 swap 函数中:当价格移动到了当前区间的边界处。此时,离开的流动性区间休眠,并激活下一个区间。
并且我们会开始下一个循环并且寻找下一个有流动性的 tick。
state.sqrtPriceX96是新的现价,即在上一个交易过后会被设置的价格;step.sqrtNextX96是下一个已初始化的tick对应的价格。- 如果它们相等,说明我们达到了这个区间的边界。
- 此时需要更新 $L$(添加或移除流动性)并且使用这个边界
next_tick作为现在的tick,继续这笔交易。
if (state.sqrtPriceX96 == step.sqrtPriceNextX96) {
if (step.initialized) {
int128 liquidityDelta = ticks.cross(step.nextTick);
if (zeroForOne) liquidityDelta = -liquidityDelta;
state.liquidity = LiquidityMath.addLiquidity(
state.liquidity,
liquidityDelta
);
if (state.liquidity == 0) revert NotEnoughLiquidity();
}
state.tick = zeroForOne ? step.nextTick - 1 : step.nextTick;
}
通常来说,当价格上涨,从左到右穿过穿过一个 tick 时:
- 因此,往右穿过一个下界
tick,表示进入新的流动性区间,会增加流动性 - 往右穿过一个上界
tick,表示离开一个流动性区间,会减少流动性- 然而如果
zeroForOne被设置为true,我们会把符号反过来:- 当价格下降时,往左跨过上界
tick,表示进入新的流动性区间,会增加流动性 - 往左跨过下界
tick,表示离开当前流动性池子, 会减少流动性
- 当价格下降时,往左跨过上界
- 然而如果
当更新 state.tick 时:
- 如果价格是下降的(
zeroForOne设置为 true), 我们需要将 tick 减一来走到下一个区间; - 而当价格上升时(
zeroForOne为 false), 根据TickBitmap.nextInitializedTickWithinOneWord,已经走到了下一个区间了。
另一个重要的改动是,当我们需要在跨过 tick 时更新流动性。全局的更新是在循环之后:
if (liquidity_ != state.liquidity) liquidity = state.liquidity;
在区间内,我们在进入/离开区间时多次更新 state.liquidity。
交易后,我们需要更新全局的 $L$ 来反应现价可用的流动性,同时避免多次写合约状态而消耗 gas。
流动性跟踪以及 tick 的跨域
现在让我们来更新 Tick 库。
首先要更改的是 Tick.Info 结构体:我们现在需要两个变量来跟踪 tick 的流动性:
struct Info {
bool initialized;
// total liquidity at tick
uint128 liquidityGross;
// amount of liqudiity added or subtracted when tick is crossed
int128 liquidityNet;
}
liquidityGross跟踪一个tick拥有的绝对流动性数量- 它用来跟踪一个 tick 是否还可用
liquidityNet,是一个有符号整数- 用来跟踪当跨越
tick时添加/移除的流动性数量
- 用来跟踪当跨越
liquidityNet 在 update 函数中设置:
function update(
mapping(int24 => Tick.Info) storage self,
int24 tick,
int128 liquidityDelta,
bool upper
) internal returns (bool flipped) {
...
tickInfo.liquidityNet = upper
? int128(int256(tickInfo.liquidityNet) - liquidityDelta)
: int128(int256(tickInfo.liquidityNet) + liquidityDelta);
}
上面我们提到的 cross 函数的功能也就是返回 liquidityNet(在后面的 milestone 我们引入更多功能时,函数会变得更复杂):
function cross(mapping(int24 => Tick.Info) storage self, int24 tick)
internal
view
returns (int128 liquidityDelta)
{
Tick.Info storage info = self[tick];
liquidityDelta = info.liquidityNet;
}
滑点保护
滑点(slippage)是指在交易之前看到的价格与交易实际执行的价格之间的价差
发出这笔交易和这个交易被打包进区块上链之间有一个延迟,取决于网络拥堵程度和花费的 gas
滑点保护解决的另一个很重要的问题是三明治攻击(sandwich attacks,也可以叫夹子攻击)
通过夹子,攻击者把你的交易包在他自己的两笔交易中间:一笔在你的交易前一笔在你的交易后。
- 在第一笔交易中,攻击者在较低价格购入
tokens,推高tokens价格 - 在被夹的用户交易中,用户被迫在更高的价格购买
tokens,并且持续推高tokens价格 - 在攻击者的第二笔交易中,攻击者用更高的价格卖出
tokens获利 - 但是被攻击者由于被更改的价格而获得了更少的
token,对应的利润都到了攻击者手里
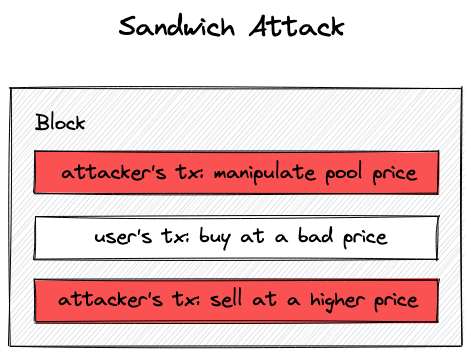
滑点保护的实现方式是,让用户选择允许实际成交价和看到的价格有多少的价差
UniswapV3 默认的滑点是 0.1%,意味着仅当实际成交价不低于现在看到价格的 99.9% 时才会成交。
这个限制比较严格,用户可以自行调整滑点的数值,在变动剧烈的时候会很有用。
接下来我们在我们的实现中加入滑点保护。
交易中的滑点保护
为了保护交易,我们需要在 swap 函数中多加一个参数:
我们希望用户设定一个停机价格,也即交易会中止的价格。我们把这个参数叫做 sqrtPriceLimitX96:
function swap(
address recipient,
bool zeroForOne,
uint256 amountSpecified,
uint160 sqrtPriceLimitX96,
bytes calldata data
) public returns (int256 amount0, int256 amount1) {
...
if (
zeroForOne
? sqrtPriceLimitX96 > slot0_.sqrtPriceX96 ||
sqrtPriceLimitX96 < TickMath.MIN_SQRT_RATIO
: sqrtPriceLimitX96 < slot0_.sqrtPriceX96 &&
sqrtPriceLimitX96 > TickMath.MAX_SQRT_RATIO
) revert InvalidPriceLimit();
...
当卖出 token $x$(zeroForOne 设置为 true),sqrtPriceLimitX96 必须在现价和最小 $\sqrt{P}$ 之间,因为卖出会使得价格下降。类似地,当卖出 token $y$ 的时候,sqrtPriceLimitX96 必须在现价和最大 $\sqrt{P}$ 之间。
在 while 循环中,我们需要满足两个条件:全部的交易数额还未被填满并且现价不等于 sqrtPriceLimtX96:
..
while (
state.amountSpecifiedRemaining > 0 &&
state.sqrtPriceX96 != sqrtPriceLimitX96
) {
...
这意味着,在 UniswapV3 中,当滑点达到最大限度的时候并不会使交易失败,而仅仅是交易部分成交。
另一个我们需要考虑滑点的地方是调用 SwapMath.computeSwapStep 时:
(state.sqrtPriceX96, step.amountIn, step.amountOut) = SwapMath
.computeSwapStep(
state.sqrtPriceX96,
(
zeroForOne
? step.sqrtPriceNextX96 < sqrtPriceLimitX96
: step.sqrtPriceNextX96 > sqrtPriceLimitX96
)
? sqrtPriceLimitX96
: step.sqrtPriceNextX96,
state.liquidity,
state.amountSpecifiedRemaining
);
在这里,我们需要确保 computeSwapStep 不会计算出一个超过滑点的交易数量——这保证了现价永远不会越过限制价格。
多池子交易
在实现了跨 tick 交易之后,已经十分接近真实的 Uniswap V3 交易了。
目前的实现中一个非常重要的限制在于,仅仅允许在同一个池子里的交易——如果某一对 token 没有池子,我们就不能在这两个 token 之间进行交易。在 Uniswap 中并不是如此,因为它允许多池子交易。在这章中,我们将在我们的实现中添加多池子交易的功能。
计划如下:
- 首先,学习并实现工厂合约;
- 接下来,将探究链式交易,或者叫做多池子交易如何工作,并实现 Path 库;
- 将会实现一个基本的路由,来寻找到两个 token 之间的路径;
- 在上述过程中,也会学到关于 tick 间隔的知识,一种优化交易的方式。
完整合约代码
工厂合约
Uniswap 由多个离散的池子合约构成,每个池子负责一对 token 的交易。
然而,仍然可以进行中间交易:
- 第一笔交易把一种 token 转换成另一种有交易对的 token
- 然后再把这种 token 转换成目标 token
这个路径可以更长并且有更多种的中间 token
*工厂(Factory)*合约是一个拥有以下功能的合约:
- 它作为池子合约的中心化注册点。在工厂中,你可以找到所有已部署的池子,对应的
token和地址。 - 它简化了池子合约的部署流程。EVM允许在智能合约中部署智能合约——工厂合约使用这个性质来让池子合约的部署变得十分简单。
- 它让池子合约的地址可预测,并且能够在注册池子之前就计算出这个地址。这让池子更容易被发现。
Tick 间隔
回顾一下我们在 swap 函数中的循环:
while (
state.amountSpecifiedRemaining > 0 &&
state.sqrtPriceX96 != sqrtPriceLimitX96
) {
...
(step.nextTick, ) = tickBitmap.nextInitializedTickWithinOneWord(...);
(state.sqrtPriceX96, step.amountIn, step.amountOut) = SwapMath.computeSwapStep(...);
...
}
这个循环通过在一个方向上遍历来寻找拥有流动性的已初始化的 tick。
- 如果一个有流动性的
tick离得很远,代码将会经过两个tick之间的所有tick,十分消耗gas - 为了让循环更节约
gas,Uniswap的池子有一个叫做tickSpacing的参数设定 - 正如其名字所示,代表两个
tick之间的距离——距离越大,越节省 gas,同时价格区间越大
然而,tick 间隔越大,精度越低。
- 价格波动性低的交易对(例如两种稳定币的池子)需要更高的精度,因为在这样的池子中价格移动很小;
- 价格波动性中等和较高的交易对可以有更低的精度,因为在这样的交易对中价格移动会很大。
- 为了处理这样的多样性,
Uniswap允许在交易对创建时设定一个tick间隔。Uniswap允许部署者在下列选项中选择:10,60,200,tick_index只能够是tickSpacing的整数倍
因此,一个池子可以由以下参数唯一确定:
function createPool(
address tokenA,
address tokenB,
uint24 fee
) external override returns (address pool) {
require(tokenA != tokenB);
(address token0, address token1) = tokenA < tokenB ? (tokenA, tokenB) : (tokenB, tokenA);
require(token0 != address(0));
int24 tickSpacing = feeAmountTickSpacing[fee];
TickSpacingExtraInfo memory info = feeAmountTickSpacingExtraInfo[fee];
require(tickSpacing != 0 && info.enabled, "fee is not available yet");
if (info.whitelistRequested) {
require(_whiteListAddresses[msg.sender], "user should be in the white list for this fee tier");
}
require(getPool[token0][token1][fee] == address(0));
pool = IPancakeV3PoolDeployer(poolDeployer).deploy(address(this), token0, token1, fee, tickSpacing);
getPool[token0][token1][fee] = pool;
// populate mapping in the reverse direction, deliberate choice to avoid the cost of comparing addresses
getPool[token1][token0][fee] = pool;
emit PoolCreated(token0, token1, fee, tickSpacing, pool);
}
可以有 token 相同但是
tickSpacing|Fee不同的池子存在。
Factory 合约 call Deploy 合约使用这组参数来作为池子的唯一定位,并且把他们作为 salt 来产生池子合约地址。
function deploy(
address factory,
address token0,
address token1,
uint24 fee,
int24 tickSpacing
) external override onlyFactory returns (address pool) {
parameters = Parameters({factory: factory, token0: token0, token1: token1, fee: fee, tickSpacing: tickSpacing});
pool = address(new PancakeV3Pool{salt: keccak256(abi.encode(token0, token1, fee))}());
delete parameters;
}
这段代码看起来很奇怪,因为 parameters 在 Deploy 合约中并没有用到
Uniswap Pool 的构造函数中需要读取该参数,因此这些参数在被使用 new 关键字部署的时候,Pool 合约会返调 Deploy 合约的参数
constructor() {
int24 _tickSpacing;
(factory, token0, token1, fee, _tickSpacing) = IPancakeV3PoolDeployer(msg.sender).parameters();
tickSpacing = _tickSpacing;
maxLiquidityPerTick = Tick.tickSpacingToMaxLiquidityPerTick(_tickSpacing);
}
池子初始化
正如上面代码所示,不再在池子的构造函数中设置当前价格sqrtPriceX96 和 tick
而是在在另一个函数 initialize 中完成,这个函数在池子部署后调用:
// src/UniswapV3Pool.sol
function initialize(uint160 sqrtPriceX96) public {
if (slot0.sqrtPriceX96 != 0) revert AlreadyInitialized();
int24 tick = TickMath.getTickAtSqrtRatio(sqrtPriceX96);
slot0 = Slot0({sqrtPriceX96: sqrtPriceX96, tick: tick});
}
这是我们现在部署池子的方式:
function createAndInitializePoolIfNecessary(
address token0,
address token1,
uint24 fee,
uint160 sqrtPriceX96
) external payable override returns (address pool) {
require(token0 < token1);
pool = IPancakeV3Factory(factory).getPool(token0, token1, fee);
if (pool == address(0)) {
pool = IPancakeV3Factory(factory).createPool(token0, token1, fee);
IPancakeV3Pool(pool).initialize(sqrtPriceX96);
} else {
(uint160 sqrtPriceX96Existing, , , , , , ) = IPancakeV3Pool(pool).slot0();
if (sqrtPriceX96Existing == 0) {
IPancakeV3Pool(pool).initialize(sqrtPriceX96);
}
}
}
交易路径
假设有以下几个池子:
WETH/USDC, USDC/USDT, WBTC/USDT。
如果想要把 WETH 换成 WBTC,需要进行多步交换(WETH→USDC→USDT→WBTC),因为没有直接的 WETH/WBTC 池子。
或者改进我们的合约来支持这样链式的,或者叫多池子的交易
当进行多池子交易时,我们会把上一笔交易的输出作为下一笔交易的输入。例如:
- 在
WETH/USDC池子,我们卖出WETH买入USDC; - 在
USDC/USDT池子,我们卖出前一笔交易得到的USDC买入USDT; - 在
WBTC/USDT池子,我们卖出前一笔交易得到的USDT买入WBTC。
我们可以把这样一个序列转换成如下路径:
WETH/USDC,USDC/USDT,WBTC/USDT
并在合约中沿着这个路径进行遍历来在同一笔交易中实现多笔交易。
然而,在兑换过程,不再需要知道池子地址,而可以通过池子参数计算出地址。
因此,上述的路径可以被转换成一系列的 token:
WETH, USDC, USDT, WBTC
并且由于 tick 间隔也是一个标识池子的参数,我们也需要把它包含在路径里:
WETH, 60, USDC, 10, USDT, 60, WBTC
其中的 60, 10 都是 tick_space 。
现在,有了这样的路径,可以遍历这条路径来获取每个池子的参数:
WETH, 60, USDC;USDC, 10, USDT;USDT, 60, WBTC.
知道了这些参数,通过 PoolAddress.computeAddress 来算出池子地址。
在一个池子内交易的时候也可以使用这个概念:路径仅包含一个池子的参数。因此,交易路径可以适用于所有类型的交易。
Path 库
在代码中,一个交易路径是一个字节序列:
bytes.concat(
bytes20(address(weth)),
bytes3(uint24(60)),
bytes20(address(usdc)),
bytes3(uint24(10)),
bytes20(address(usdt)),
bytes3(uint24(60)),
bytes20(address(wbtc))
);
它长这样:
0xC02aaA39b223FE8D0A0e5C4F27eAD9083C756Cc2 # weth address
00003c # 60
A0b86991c6218b36c1d19D4a2e9Eb0cE3606eB48 # usdc address
00000a # 10
dAC17F958D2ee523a2206206994597C13D831ec7 # usdt address
00003c # 60
2260FAC5E5542a773Aa44fBCfeDf7C193bc2C599 # wbtc address
以下是我们需要实现的函数:
- 计算路径中池子的数量;
- 看一个路径是否包含多个池子;
- 提取路径中第一个池子的参数;
- 进入路径中的下一个 token 对;
- 解码池子参数
计算路径中池子的数量
首先实现计算路径中池子的数量:
// src/lib/Path.sol
library Path {
/// @dev The length the bytes encoded address
uint256 private constant ADDR_SIZE = 20;
/// @dev The length the bytes encoded tick spacing
uint256 private constant TICKSPACING_SIZE = 3;
/// @dev The offset of a single token address + tick spacing
uint256 private constant NEXT_OFFSET = ADDR_SIZE + TICKSPACING_SIZE;
/// @dev The offset of an encoded pool key (tokenIn + tick spacing + tokenOut)
uint256 private constant POP_OFFSET = NEXT_OFFSET + ADDR_SIZE;
/// @dev The minimum length of a path that contains 2 or more pools;
uint256 private constant MULTIPLE_POOLS_MIN_LENGTH =
POP_OFFSET + NEXT_OFFSET;
...
我们首先定义一系列常量:
ADDR_SIZE是地址的大小,20字节;TICKSPACING_SIZE是tick间隔的大小,3字节(uint24);NEXT_OFFSET是到下一个token地址的偏移——为了获取这个地址,我们要跳过当前地址和tick间隔;POP_OFFSET是编码的池子参数的偏移 (token0 address + tick spacing + token1 address);MULTIPLE_POOLS_MIN_LENGTH是包含两个或以上池子的路径长度 (一个池子的参数 + tick_space + token address)。
为了计算路径中的池子数量,我们减去一个地址的大小(路径中的第一个或最后一个 token)并且用剩下的值除以 NEXT_OFFSET 即可:
function numPools(bytes memory path) internal pure returns (uint256) {
return (path.length - ADDR_SIZE) / NEXT_OFFSET;
}
判断一个路径是否有多个池子
为了判断一个路径中是否有多个池子,我们只需要将路径长度与 MULTIPLE_POOLS_MIN_LENGTH 比较即可:
function hasMultiplePools(bytes memory path) internal pure returns (bool) {
return path.length >= MULTIPLE_POOLS_MIN_LENGTH;
}
提取路径中第一个池子的参数
因为 Solidity 没有原生的 bytes 操作函数,
从一个字节数组中提取出一个子数组的函数,以及将 address 和 uint24 转换成字节的函数。
幸运的是,已经有一个叫做 solidity-bytes-utils 的开源库实现了这些。为了使用这个库,我们需要扩展 Path 库里面的 bytes 类型:
library Path {
using BytesLib for bytes;
...
}
现在可以实现 getFirstPool 了:
function getFirstPool(bytes memory path)
internal
pure
returns (bytes memory)
{
return path.slice(0, POP_OFFSET);
}
这个函数仅仅返回了 token address + tick spacing + token address 这一段字节。
前往路径中下一个 token 对
在遍历路径的时候使用下面这个函数,来扔掉已经处理过的池子。
注意,移除的是 token address + tick spacing,而不是完整的池子参数,
因为还需要另一个 token 地址来计算下一个池子的地址。
function skipToken(bytes memory path) internal pure returns (bytes memory) {
return path.slice(NEXT_OFFSET, path.length - NEXT_OFFSET);
}
解码第一个池子的参数
最后,我们需要解码路径中第一个池子的参数:
function decodeFirstPool(bytes memory path)
internal
pure
returns (
address tokenIn,
address tokenOut,
uint24 tickSpacing
)
{
tokenIn = path.toAddress(0);
tickSpacing = path.toUint24(ADDR_SIZE);
tokenOut = path.toAddress(NEXT_OFFSET);
}
遗憾的是,BytesLib 没有实现 toUint24 这个函数,但可以自己实现它!
在 BytesLib 中有很多 toUintXX 这样的函数,可以把其中一个转换成 uint24 类型的:
library BytesLibExt {
function toUint24(bytes memory _bytes, uint256 _start)
internal
pure
returns (uint24)
{
require(_bytes.length >= _start + 3, "toUint24_outOfBounds");
uint24 tempUint;
assembly {
tempUint := mload(add(add(_bytes, 0x3), _start))
}
return tempUint;
}
}
多池子交易
在合约中实现多池子交易。
更新管理员合约
单池和多池交易
struct SwapSingleParams {
address tokenIn;
address tokenOut;
uint24 tickSpacing;
uint256 amountIn;
uint160 sqrtPriceLimitX96;
}
struct SwapParams {
bytes path;
address recipient;
uint256 amountIn;
uint256 minAmountOut;
}
SwapSingleParams的参数为池子参数、输入数量,以及一个限制价格——这与我们之前的基本一致。SwapParams的参数为路径、输出金额接受方、输入数量,以及最小输出数量。 最后一个参数替代了sqrtPriceLimitX96,因为在多池子交易中不再能使用池子合约中的滑点保护 (使用限价机制实现)- 我们需要另实现一个滑点保护,检查最终的输出数量并且与
minAmountOut对比: 当最终输出数量小于minAmountOut的时候交易会失败。
核心交易逻辑
我们现在实现一个内部的 _swap 函数,会被单池交易和多池交易的函数调用。它的功能就是准备参数并且调用 Pool.swap:
function _swap(
uint256 amountIn,
address recipient,
uint160 sqrtPriceLimitX96,
SwapCallbackData memory data
) internal returns (uint256 amountOut) {
SwapCallbackData 是一个新的数据结构,
包含需要在 swap 函数和 UniswapV3Callback 之间传递的数据:
struct SwapCallbackData {
bytes path;
address payer;
}
path 是交易路径,payer 是在这笔交易中付出 token 的地址——在多池交易中这个付款者会有所不同。
在 _swap 中要做的第一件事就是使用 Path 库来提取池子参数:
// function _swap(...) {
(address tokenIn, address tokenOut, uint24 tickSpacing) = data
.path
.decodeFirstPool();
然后确认交易方向:
bool zeroForOne = tokenIn < tokenOut;
接下来执行真正的交易:
在这里调用 getPool 来找到池子,调用池子的 swap 函数
// function _swap(...) {
(int256 amount0, int256 amount1) = getPool(
tokenIn,
tokenOut,
tickSpacing
).swap(
recipient,
zeroForOne,
amountIn,
sqrtPriceLimitX96 == 0
? (
zeroForOne
? TickMath.MIN_SQRT_RATIO + 1
: TickMath.MAX_SQRT_RATIO - 1
)
: sqrtPriceLimitX96,
abi.encode(data)
);
单池交易
swapSingle 仅仅是 _swap 包装起来而已:
function swapSingle(SwapSingleParams calldata params)
public
returns (uint256 amountOut)
{
amountOut = _swap(
params.amountIn,
msg.sender,
params.sqrtPriceLimitX96,
SwapCallbackData({
path: abi.encodePacked(
params.tokenIn,
params.tickSpacing,
params.tokenOut
),
payer: msg.sender
})
);
}
注意到在这里构造了一个单池的路径:单池交易是仅有一个池子的多池交易。
多池交易
多池交易仅仅比单池交易复杂一点
function swap(SwapParams memory params) public returns (uint256 amountOut) {
address payer = msg.sender;
bool hasMultiplePools;
...
第一笔交易是由用户付费,因为用户提供最开始输入的 token。
接下来,开始遍历路径中的池子:
while (true) {
hasMultiplePools = params.path.hasMultiplePools();
params.amountIn = _swap(
params.amountIn,
hasMultiplePools ? address(this) : params.recipient,
0,
SwapCallbackData({
path: params.path.getFirstPool(),
payer: payer
})
);
...
在每一次循环中,用这些参数调用 _swap 函数:
params.amountIn跟踪输入的数量。- 在第一笔交易中这个数量由用户提供
- 在后面的交易中这个数量是来自于前一笔交易的输出数量。
hasMultiplePools ? address(this) : params.recipient- 如果路径中有多个池子,收款方是管理合约,它存储中间交易得到的
token。 - 如果在路径中仅剩一个交易(最后一笔),收款人应该是之前参数中设定的地址(通常是创建交易的人)。
- 如果路径中有多个池子,收款方是管理合约,它存储中间交易得到的
sqrtPriceLimitX96设置为 0,来禁用池子合约中的滑点保护- 最后一个参数是传递给
uniswapV3SwapCallback
在完成一笔交易后,需要前往路径中的下一个池子,或者返回.
在这里修改付款人并且从路径中移除已处理的池子:
...
if (hasMultiplePools) {
payer = address(this);
params.path = params.path.skipToken();
} else {
amountOut = params.amountIn;
break;
}
}
最后,新的滑点保护:
if (amountOut < params.minAmountOut)
revert TooLittleReceived(amountOut);
Swap Callback
function uniswapV3SwapCallback(
int256 amount0,
int256 amount1,
bytes calldata data_
) public {
SwapCallbackData memory data = abi.decode(data_, (SwapCallbackData));
(address tokenIn, address tokenOut, ) = data.path.decodeFirstPool();
bool zeroForOne = tokenIn < tokenOut;
int256 amount = zeroForOne ? amount0 : amount1;
if (data.payer == address(this)) {
IERC20(tokenIn).transfer(msg.sender, uint256(amount));
} else {
IERC20(tokenIn).transferFrom(
data.payer,
msg.sender,
uint256(amount)
);
}
}
callback 函数在 data_ 段获得包含路径和付款人地址的 SwapCallbackData。
它从路径中提取 token 地址,识别交易方向,以及该合约需要转出的金额。
接下来,它根据付款人的不同而进行不同行为:
- 如果付款人是当前合约(在连续交易时,当前合约作为中间人),它直接将本合约账户下的
token转到下一个池子(调用这个callback的池子)。 - 如果付款人是一个不同的地址(创建交易的用户),它从用户那里把
token转给池子。
费率和价格预言机
本章添加交易费率(swap fees) 和一个价格预言机(price oracle):
- 交易费率是我们实现的 DEX 中一个关键的机制。它能够使一切事情联合起来共同运作。交易费率能够激励 LP 提供流动性,没有流动性就无法进行交易。
- 一个价格预言机,这只是 DEX 的一个可选功能。一个 DEX 除了能够执行交易之外,也能够作为一个价格预言机——向其他服务提供 token 的价格。这实际上并不影响我们交易的执行,但是它对于其他链上应用来说是一个很有用的服务。
完整合约代码
交易费率
正如简介中所说,交易费率是 Uniswap 的一个核心机制。
LP需要从提供流动性中获得收益- 每一笔
swap中都会付出一小笔费用,这些费用将会按提供的流动性占比分配给在交易价格上提供流动性的LP。
手续费
在 V2 中,因为大家提供的流动性都是统一的手续费标准(0.3%),统一的价格区间(0, ∞):
- 所以大家的资金都是均匀分布在整个价格轴之上的,
- 因此在每一笔交易的过程中,大家收取手续费的权重计算比例也应该是相等的。
- 即每一笔手续费的收益分配,只基于用户提供的流动性相对于总流动性的比例来分配,出资多的得到的收益多。
然而 V3 的价格区间做市机制,让流动性都有不同的做市区间:
- 也就是说不同的交易价格,使用的流动性是不同的
- 那么这个时候,再用出资比例来分配,是不合适的
正确的方式应该是记录每一笔交易,都使用了哪些流动性头寸 position(tick_index),再将这么些头寸汇总,按比例分配。
这样在理论上来说是合理的,如果是中心化的网络这么干的成本可能承受的起, 但放到区块链的运行环境中,频繁的进行高昂的读写操作是不可行的,会为用户带来极高的 gas 费用, 使得交易的摩擦成本飙升,变得不划算。
费率如何收集
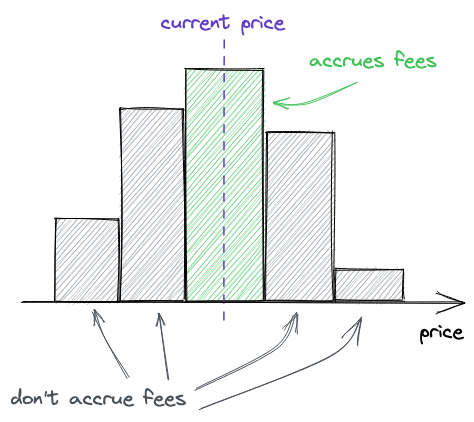
交易费用仅仅当一个价格区间在使用中的时候才会被收集到这个区间中。
- 当价格上升,
tick穿过价格区间的下界;表示因为价格上涨,向右进入新的tick区间; - 当价格下降,
tick穿过价格区间的上界;表示因为价下跌,向左进入新的tick区间;
而在下列的时刻一个价格区间被停用:
- 当价格上升,
tick穿过价格区间的上界,表示因为价格上涨离开当前tick区间; - 当价格下降,
tick穿过价格区间的下界;
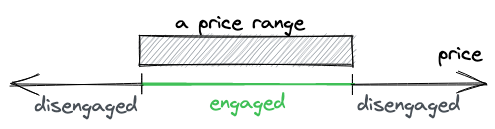
除了知道何时一个区间会被激活/停用以外,还希望能够跟踪每个价格区间累积了多少费用。
为了让费用计算更简单,Uniswap V3 跟踪swap交易产生的总手续费。
之后,价格区间的费用通过总费用计算出来: 总手续费减去价格区间之外累计的费用。
计算 Position(a,b) 累积费用
为了计算一个 position 累计的总费用,我们需要考虑两种情况:
当现价在这个区间内:
减去到目前为止,这些 tick 之外累积的费用:
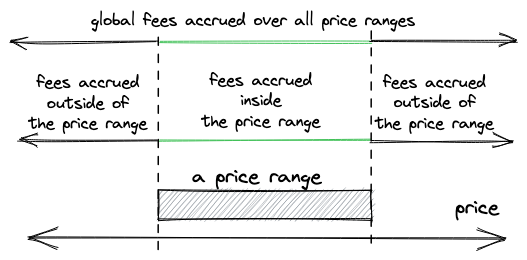
feeGrowthInside = feeGrowthGlobal - feeGrowthOutside_below - feeGrowthOutside_above
feeGrowthOutside_below 对应 (0, a) 区间, feeGrowthOutside_above 对应 (b, ∞) 区间。
当现价不在这个区间内:
假设我们需要计算 a, b 两点区间内的手续费,此时 i_current 当前在 b 点右侧。
| . | . | . | . | . | . | . | . |
|---|---|---|---|---|---|---|---|
| … | a | b | i | … |
i_current 当前在 b 点右侧,此时 feeGrowthOutside_b 实际上记录的是 b 点左侧的手续费,而我们需要计算的 above 应该是 b 点右侧的手续费,所以这里其实是需要用 feeGrowthGlobal 减去 feeGrowthOutside_b.
feeGrowthOutside_below = feeGrowthOutside_a // a点所对应的tick的feeGrowthOutside
feeGrowthOutside_above = feeGrowthGlobal - feeGrowthOutside_b // b点所对应的tick的feeGrowthOutside
代入之前的公式
feeGrowthInside = feeGrowthGlobal - feeGrowthOutside_a - (feeGrowthGlobal - feeGrowthOutside_b)
注意根据 i_current, a, b 三者位置关系不同,需要判断 above 和 below 的计算方式,具体逻辑在 Tick.sol 的 getFeeGrowInside() 中。
有流动性注入
在价格的边界对应的 tick 上有如下初始化规则:
🎯 规则说明
- 当
tick<= 当前价格(i <= i_current)时,我们认为该tick是“在上方”。feeGrowthOutside = feeGrowthGlobal
- 当
tick> 当前价格(i > i_current)时,我们认为该tick是“在下方”。feeGrowthOutside = 0
if (liquidityGrossBefore == 0) {
// by convention, we assume that all growth before a tick was initialized happened _below_ the tick
if (tick <= tickCurrent) {
info.feeGrowthOutside0X128 = feeGrowthGlobal0X128;
info.feeGrowthOutside1X128 = feeGrowthGlobal1X128;
info.secondsPerLiquidityOutsideX128 = secondsPerLiquidityCumulativeX128;
info.tickCumulativeOutside = tickCumulative;
info.secondsOutside = time;
}
info.initialized = true;
}
🧪 示例 1:
添加流动性区间: (tickLower=100, tickUpper=200)
当前 tick(i_current)= 150
feeGrowthGlobal = 1000
初始化两个 tick:
| Tick | 相对位置 | 设置 feeGrowthOutside |
|---|---|---|
| 100 | ≤ 当前价格 | 1000 |
| 200 | > 当前价格 | 0 |
tick[100].feeGrowthOutside = 1000;
tick[200].feeGrowthOutside = 0;
Cross-tick交易
feeGrowthOutside 有如下更新规则:
- 当价格穿过某个已初始化的
tick时,该tick上的feeGrowthOutside需要翻转,因为外侧手续费永远要在当前价格的另一侧 feeGrowthOutside = feeGrowthGlobal - feeGrowthOutside
function cross(
mapping(int24 => Tick.Info) storage self,
int24 tick,
uint256 feeGrowthGlobal0X128,
uint256 feeGrowthGlobal1X128,
uint160 secondsPerLiquidityCumulativeX128,
int56 tickCumulative,
uint32 time
) internal returns (int128 liquidityNet) {
Tick.Info storage info = self[tick];
info.feeGrowthOutside0X128 = feeGrowthGlobal0X128 - info.feeGrowthOutside0X128;
info.feeGrowthOutside1X128 = feeGrowthGlobal1X128 - info.feeGrowthOutside1X128;
...
示例
✅ 基础设定
- 初始全局手续费:
feeGrowthGlobal = 100 - 起始
tick:tick = 150 - 两段流动性区间(即
LP添加的流动性):- 区间
A-B:[100, 200),tick a=100,tick b=200 - 区间
C-D:[300, 400),tick c=300,tick d=400
- 区间
手续费变化过程:
- 价格从
tick 150开始 - 跨过
tick 200→ 进入tick区间C-D前,还会有一个从feeGrowthGlobal = 180到300 - 继续上升后进入区间
C-D,feeGrowthGlobal = 500
阶段 0:初始化时 tick = 150,feeGrowthGlobal = 100
- tick a = 100(左边)⇒ feeGrowthOutside = 100
- tick b = 200(右边)⇒ feeGrowthOutside = 0
- tick c = 300(右边)⇒ feeGrowthOutside = 0
- tick d = 400(右边)⇒ feeGrowthOutside = 0
1 swap在(a,b)
在 (a,b)执行 swap, glb = 100 +80 = 180
feeGrowthInside(a,b) = feeGrowthGlobal - feeGrowthOutside_a - feeGrowthOutside_b = 180 - 100 - 0 = 80
2 价格上涨后跨到 (c,d)区间
在 (a,b)-> (c,d)执行 swap, glb = 180->300->500
Cross b: tick[b].feeGrowthOutside = feeGrowthGlobal - feeGrowthOutside= 300 - 0 = 300
cross c: tick[c].feeGrowthOutside = feeGrowthGlobal - feeGrowthOutside= 300 - 0 = 300
手续费计算:
function getFeeGrowthInside(
mapping(int24 => Tick.Info) storage self,
int24 tickLower,
int24 tickUpper,
int24 tickCurrent,
uint256 feeGrowthGlobal0X128,
uint256 feeGrowthGlobal1X128
) internal view returns (uint256 feeGrowthInside0X128, uint256 feeGrowthInside1X128) {
Info storage lower = self[tickLower];
Info storage upper = self[tickUpper];
// calculate fee growth below
uint256 feeGrowthBelow0X128;
uint256 feeGrowthBelow1X128;
if (tickCurrent >= tickLower) {
feeGrowthBelow0X128 = lower.feeGrowthOutside0X128;
feeGrowthBelow1X128 = lower.feeGrowthOutside1X128;
} else {
feeGrowthBelow0X128 = feeGrowthGlobal0X128 - lower.feeGrowthOutside0X128;
feeGrowthBelow1X128 = feeGrowthGlobal1X128 - lower.feeGrowthOutside1X128;
}
// calculate fee growth above
uint256 feeGrowthAbove0X128;
uint256 feeGrowthAbove1X128;
if (tickCurrent < tickUpper) {
feeGrowthAbove0X128 = upper.feeGrowthOutside0X128;
feeGrowthAbove1X128 = upper.feeGrowthOutside1X128;
} else {
feeGrowthAbove0X128 = feeGrowthGlobal0X128 - upper.feeGrowthOutside0X128;
feeGrowthAbove1X128 = feeGrowthGlobal1X128 - upper.feeGrowthOutside1X128;
}
feeGrowthInside0X128 = feeGrowthGlobal0X128 - feeGrowthBelow0X128 - feeGrowthAbove0X128;
feeGrowthInside1X128 = feeGrowthGlobal1X128 - feeGrowthBelow1X128 - feeGrowthAbove1X128;
}
此时, (a,b) 区间的手续费:
当价格已经不在计算的价格区间内时:手续费的计算已经和 总手续费无关,只跟区间的手续费差有关
P_a < P_current, feeGrowthBelow = P_a.feeGrowthBelow = 100
P_a < P_current, feeGrowthAboveX128 = feeGrowthGlobalX128 - P_b.feeGrowthOutsideX128 = 500 - 300 = 200
Fee(a,b) = feeGrowthGlobalX128 - P_a.feeGrowthBelow - feeGrowthGlobalX128 + P_b.feeGrowthOutsideX128
= P_b.feeGrowthOutsideX128 - P_a.feeGrowthBelow
= 300 -100 = 200
此时, (c,d) 区间的手续费:
P_c < P_current, feeGrowthBelow = P_c.feeGrowthBelow = 300
P_current < P_d, feeGrowthAboveX128 = P_d.feeGrowthOutside128 = 0
Fee(c,d) = 500 - 300 - 0 = 200
规则回顾
- 用户
swap token的时候支付费用。输入token中的一小部分将会被减去,并累积到池子的余额中。 - 每个池子都有
feeGrowthGlobal0X128和feeGrowthGlobal1X128两个状态变量,来跟踪每单位的流动性累计的总费用(也即,总的费用除以池子流动性)。 tick跟踪在它之外累积的费用
- 当添加一个新的位置并激活一个 tick 的时候
- tick 位置价格高于现价 slot0.tick,
feeGrowthOutside = 0 - tick 位置价格高小于等于现价 slot0.tick,
feeGrowthOutside = fee_global
- tick 位置价格高于现价 slot0.tick,
- 每当一个
tick被cross时,在这个tick之外积累的费用就会更新为:
feeGrowthOutside = feeGrowthGlobal - feeGrowthOutside
tick知道了在他之外累积了多少费用,就可以让我们计算出在一个position内部累积了多少费用(position就是两个tick之间的区间)。- 知道了一个
position内部累积了多少费用,就能够计算LP能够分成到多少费用。
- 如果一个
position没有参与到交易中,它的累计费率会是 0 - 在这个区间提供流动性的 LP 将不会获得任何利润。
累积交易费用
概念说明
🧱 背景概念简述
tick:UniswapV3 将价格空间离散化为一系列整数 tick,价格变动就是 tick 的移动。
feeGrowthGlobal:表示当前池子整体累计的手续费增长。
feeGrowthOutside:记录某个 tick 外部(价格另一侧)的手续费累计值,用于精准分配 LP 收益。
i_current:当前价格对应的 tick。
tick 边界流动性注入:即为流动性区间设置上下边界(tick_lower, tick_upper)。
添加需要的状态变量
需要做的第一件事是在池子中添加费率参数——每个池子都有一个固定且不可变的费率,在部署时配置。
费率和 tick 间隔绑定:费率越高,tick 间隔越大。
这是因为稳定性越高的池子(稳定币池)的费率应该更低。
让我们更新工厂合约:
// src/UniswapV3Factory.sol
contract UniswapV3Factory is IUniswapV3PoolDeployer {
...
mapping(uint24 => uint24) public fees; // `tickSpacings` replaced by `fees`
constructor() {
fees[500] = 10;
fees[3000] = 60;
}
function createPool(
address tokenX,
address tokenY,
uint24 fee
) public returns (address pool) {
...
parameters = PoolParameters({
factory: address(this),
token0: tokenX,
token1: tokenY,
tickSpacing: fees[fee],
fee: fee
});
...
}
}
费率的单位是基点的百分之一,也即一个费率单位是 0.0001%,500 是 0.05%,3000 是 0.3%。
下一步是在池子中累积交易费用。为们要添加两个全局费用累积的变量:
// src/UniswapV3Pool.sol
contract UniswapV3Pool is IUniswapV3Pool {
...
uint24 public immutable fee;
uint256 public feeGrowthGlobal0X128;
uint256 public feeGrowthGlobal1X128;
}
在 tick 中更新费用追踪器
接下来,需要在 tick 中更新费用追踪器(当交易中穿过一个 tick 时):
if (state.sqrtPriceX96 == step.sqrtPriceNextX96) {
int128 liquidityDelta = ticks.cross(
step.nextTick,
(
zeroForOne
? state.feeGrowthGlobalX128
: feeGrowthGlobal0X128
),
(
zeroForOne
? feeGrowthGlobal1X128
: state.feeGrowthGlobalX128
)
);
...
}
由于此时还没有更新 feeGrowthGlobal0X128/feeGrowthGlobal1X128 状态变量,可以把 state.feeGrowthGlobalX128 作为其中一个参数传入。cross 函数更新费用追踪器:
// src/lib/Tick.sol
function cross(
mapping(int24 => Tick.Info) storage self,
int24 tick,
uint256 feeGrowthGlobal0X128,
uint256 feeGrowthGlobal1X128
) internal returns (int128 liquidityDelta) {
Tick.Info storage info = self[tick];
info.feeGrowthOutside0X128 =
feeGrowthGlobal0X128 -
info.feeGrowthOutside0X128;
info.feeGrowthOutside1X128 =
feeGrowthGlobal1X128 -
info.feeGrowthOutside1X128;
liquidityDelta = info.liquidityNet;
}
更新全局费用追踪器
最后一步,当交易完成时,需要更新全局的费用追踪:
if (zeroForOne) {
feeGrowthGlobal0X128 = state.feeGrowthGlobalX128;
} else {
feeGrowthGlobal1X128 = state.feeGrowthGlobalX128;
}
同样地,在一笔交易中只有一个变量会更新,因为交易费仅从输入 token 中收取。
更新 position 费用和 token 数量
下一步是计算 position 累计的费用和 token 数量。
由于一个 position 就是两个 tick 之间的一个区间,可以使用 tick 中的费用追踪器来计算这些值。
得到 position 内累积的费用后,就可以更新 position 内的费用和数量追踪器了:
// src/lib/Position.sol
function update(
Info storage self,
int128 liquidityDelta,
uint256 feeGrowthInside0X128,
uint256 feeGrowthInside1X128
) internal {
uint128 tokensOwed0 = uint128(
PRBMath.mulDiv(
feeGrowthInside0X128 - self.feeGrowthInside0LastX128,
self.liquidity,
FixedPoint128.Q128
)
);
uint128 tokensOwed1 = uint128(
PRBMath.mulDiv(
feeGrowthInside1X128 - self.feeGrowthInside1LastX128,
self.liquidity,
FixedPoint128.Q128
)
);
self.liquidity = LiquidityMath.addLiquidity(
self.liquidity,
liquidityDelta
);
self.feeGrowthInside0LastX128 = feeGrowthInside0X128;
self.feeGrowthInside1LastX128 = feeGrowthInside1X128;
if (tokensOwed0 > 0 || tokensOwed1 > 0) {
self.tokensOwed0 += tokensOwed0;
self.tokensOwed1 += tokensOwed1;
}
}
移除流动性
移除流动性。与 mint 相对应,我们把这个函数叫做 burn。
这个函数允许 LP 移除一个 position 中部分或者全部的流动性。
除此之外,它也会计算 LP 应该得到的利润收入。
然而,实际的 token 转移会在另一个函数中实现——collect。
燃烧流动性
燃烧流动性与铸造相反。
为了实现
burn,需要重构代码,把 position 管理相关的代码(更新 tick 和 position,以及 token 数量的计算)移动到_modifyPosition函数中,这个函数会被mint和burn使用。
function burn(
int24 lowerTick,
int24 upperTick,
uint128 amount
) public returns (uint256 amount0, uint256 amount1) {
(
Position.Info storage position,
int256 amount0Int,
int256 amount1Int
) = _modifyPosition(
ModifyPositionParams({
owner: msg.sender,
lowerTick: lowerTick,
upperTick: upperTick,
liquidityDelta: -(int128(amount))
})
);
amount0 = uint256(-amount0Int);
amount1 = uint256(-amount1Int);
if (amount0 > 0 || amount1 > 0) {
(position.tokensOwed0, position.tokensOwed1) = (
position.tokensOwed0 + uint128(amount0),
position.tokensOwed1 + uint128(amount1)
);
}
emit Burn(msg.sender, lowerTick, upperTick, amount, amount0, amount1);
}
在 burn 函数中,首先更新 position,并从中移除一定数量的流动性。
接下来,更新这个 position 应得的 token 数量
- 它包含提供流动性时转入的
token数量以及费用收入。 - 也可以把它看做把
position流动性转换到token的过程 - 这些
token将不会再被用于流动性,并且可以通过调用collect函数来赎回:
function collect(
address recipient,
int24 lowerTick,
int24 upperTick,
uint128 amount0Requested,
uint128 amount1Requested
) public returns (uint128 amount0, uint128 amount1) {
Position.Info memory position = positions.get(
msg.sender,
lowerTick,
upperTick
);
amount0 = amount0Requested > position.tokensOwed0
? position.tokensOwed0
: amount0Requested;
amount1 = amount1Requested > position.tokensOwed1
? position.tokensOwed1
: amount1Requested;
if (amount0 > 0) {
position.tokensOwed0 -= amount0;
IERC20(token0).transfer(recipient, amount0);
}
if (amount1 > 0) {
position.tokensOwed1 -= amount1;
IERC20(token1).transfer(recipient, amount1);
}
emit Collect(
msg.sender,
recipient,
lowerTick,
upperTick,
amount0,
amount1
);
}
协议费率
“Uniswap 如何盈利?”。事实上,它并不盈利(至少到 2022 年 9 月为止还没有)。
在已经完成的实现中,swap 会给 LP 支付一定手续费
每个 Uniswap 池子都有一个协议费率的机制。
协议费用从交易费用中收取:一小部分的交易费用会被用来作为协议的费用,之后会被工厂合约的所有者( Uniswap Labs )提取。
协议费率的大小是由 UNI 币的持有者来决定的,但是它必须在交易费率的 $1/4$ 到 $1/10$(包含) 之间。
协议费率大小存储在 slot0 中:
// UniswapV3Pool.sol
struct Slot0 {
...
// the current protocol fee as a percentage of the swap fee taken on withdrawal
// represented as an integer denominator (1/x)%
uint8 feeProtocol;
...
}
需要一个全局变量来追踪已经获得的协议收入:
function initialize(uint160 sqrtPriceX96) external override {
require(slot0.sqrtPriceX96 == 0, 'AI');
int24 tick = TickMath.getTickAtSqrtRatio(sqrtPriceX96);
(uint16 cardinality, uint16 cardinalityNext) = observations.initialize(_blockTimestamp());
slot0 = Slot0({
sqrtPriceX96: sqrtPriceX96,
tick: tick,
observationIndex: 0,
observationCardinality: cardinality,
observationCardinalityNext: cardinalityNext,
feeProtocol: 209718400, // default value for all pools, 3200:3200, store 2 uint32 inside
unlocked: true
});
if (fee == 100) {
slot0.feeProtocol = 216272100; // value for 3300:3300, store 2 uint32 inside
} else if (fee == 500) {
slot0.feeProtocol = 222825800; // value for 3400:3400, store 2 uint32 inside
} else if (fee == 2500) {
slot0.feeProtocol = 209718400; // value for 3200:3200, store 2 uint32 inside
} else if (fee == 10000) {
slot0.feeProtocol = 209718400; // value for 3200:3200, store 2 uint32 inside
}
emit Initialize(sqrtPriceX96, tick);
}
协议费率在 setFeeProtocol 函数中设置:
function setFeeProtocol(uint32 feeProtocol0, uint32 feeProtocol1) external override lock onlyFactoryOrFactoryOwner {
require(
(feeProtocol0 == 0 || (feeProtocol0 >= 1000 && feeProtocol0 <= 4000)) &&
(feeProtocol1 == 0 || (feeProtocol1 >= 1000 && feeProtocol1 <= 4000))
);
uint32 feeProtocolOld = slot0.feeProtocol;
slot0.feeProtocol = feeProtocol0 + (feeProtocol1 << 16);
emit SetFeeProtocol(feeProtocolOld % PROTOCOL_FEE_SP, feeProtocolOld >> 16, feeProtocol0, feeProtocol1);
}
最后,工厂合约的拥有者可以通过调用 collectProtocol 来收集累积的协议费用:
function collectProtocol(
address recipient,
uint128 amount0Requested,
uint128 amount1Requested
) external override lock onlyFactoryOwner returns (uint128 amount0, uint128 amount1) {
amount0 = amount0Requested > protocolFees.token0 ? protocolFees.token0 : amount0Requested;
amount1 = amount1Requested > protocolFees.token1 ? protocolFees.token1 : amount1Requested;
if (amount0 > 0) {
if (amount0 == protocolFees.token0) amount0--;
protocolFees.token0 -= amount0;
TransferHelper.safeTransfer(token0, recipient, amount0);
}
if (amount1 > 0) {
if (amount1 == protocolFees.token1) amount1--;
protocolFees.token1 -= amount1;
TransferHelper.safeTransfer(token1, recipient, amount1);
}
emit CollectProtocol(msg.sender, recipient, amount0, amount1);
}
价格预言机
要在 DEX 中添加的最后一个机制就是价格预言机。
什么是价格预言机?
价格预言机 Oracle 是向区块链提供资产价格的一种机制。
Uniswap V2 Oracle
UniswapV2 需要用户自己实现价格累计的功能合约
function snapshot(IUniswapV2Pair uniswapV2pair) public {
require(getTimeElapsed() >= 1 hours, "snapshot is not stale");
// we don't use the reserves, just need the last timestamp update
(, , lastSnapshotTime) = uniswapV2pair.getReserves();
snapshotPrice0Cumulative = uniswapV2pair.price0CumulativeLast();
}
V2 中跟踪累积价格,也即这个池子合约历史中每秒的价格之和。
$$a_{i} = \sum_{i=1}^t p_{i}$$
这个方法让我们能够找到两个时间点($t_1$ 和 $t_2$)之间的时间加权平均价格(TWAP),只需要将这两个时间点的累积价格($a_{t_1}$ 和 $a_{t_2}$)相减,除以他们之间相隔的秒数即可:
$$p_{t_1,t_2} = \frac{a_{t_2} - a_{t_1}}{t_2 - t_1}$$
Uniswap V3 oracle
Core Accumulator checkpoints
Uniswap v3 pool 中记录以观测值数组的形式存储。
最初,每个 pool 仅跟踪单个观测值,并随着区块的生成进行覆盖。
这限制了用户可以访问过去数据的时间。
但是,任何愿意支付交易费的一方都可以增加跟踪观测值的数量(最多为65535),从而将数据可用时间延长至约 9 天或更长时间。
将价格和流动性历史记录直接存储在池合约中,可以大大降低调用合约出现逻辑错误的可能性,并通过消除存储历史值的需要来降低集成成本。此外,v3 预言机的最大长度相当大,这使得预言机价格操纵变得更加困难,因为调用合约可以低成本地在预言机数组长度以内(或完全包含)的任意范围内构建时间加权平均值。
在 V3 中,略有一些不同。累积的价格通过 tick 来计算的(也即价格的 $log_{1.0001}$):
$$a_{i} = \sum_{i=1}^t log_{1.0001}P(i)$$
这里的 log 数值后面其实还有一个 * 1s 即以每秒作为时间间隔。
然而实际情况中,合约中是以区块的时间戳作为标记时间的,所以合约中的代码跟公式不同。
每个区块的头一笔交易时更新,此时距离上一次更新时间间隔肯定大于 1s,所以需要将更新值乘以两个区块的时间戳的差。
tickCumulative 是 tick 序号的累计值,tick 的序号就是 log(√price, 1.0001)。
tickCumulative += tick_current * delta_time
tickCumulative += tick_current * (blocktimestamp_current - blocktimestamp_before)
当外部用户使用时,求 t1 到 t2 时间内的时间加权价格 p(t1,t2) ,需要计算两个时间点的累计值的差 a(t2) - a(t1) 除以时间差。
$$
a_{t2}-a_{t1} = \frac{\sum_{i=t1}^{t2}log_{1.0001}(p_i)}{t2-t1}
$$
$$ log_{1.0001}(p_{t1,t2}) = \frac{a_{t2}-a_{t1}}{t2-t1} $$
$$ p_{t1,t2} = {1.0001}^\frac{a_{t2}-a_{t1}}{t2-t1} $$
使用几何平均的原因:
- 因为合约中记录了 tick 序号,序号是整型,且跟价格相关,所以直接计算序号更加节省 gas。(全局变量中存储的不是价格,而是根号价格,如果直接用价格来记录,要多比较复杂的计算)
- V2 中算数平均价格并不总是倒数关系(以 token1 计价 token0,或反过来),所以需要记录两种价格。V3 中使用几何平均不存在该问题,只需要记录一种价格。
- 举个例子,在 V2 中如果 USD/ETH 价格在区块 1 中是 100,在区块 2 中是 300,USD/ETH 的均价是 200 USD/ETH,但是 ETH/USD 的均价是 1/150
- 几何平均比算数平均能更好的反应真实的价格,受短期波动影响更小。白皮书中的引用提到在几何布朗运动中,算数平均会受到高价格的影响更多。
Tick 上辅助预言机计算的数据
每个已初始化的 tick 上(有流动性添加的),不光有流动性数量和手续费相关的变量(liquidityNet, liquidityGross, feeGrowthOutside),还有三个可用于做市策略。
tick 变量一览:
| Type | Variable Name | 含义 |
|---|---|---|
| int128 | liquidityNet | 流动性数量净含量 |
| int128 | liquidityGross | 流动性数量总量 |
| int256 | feeGrowthOutside0X128 | 以 token0 收取的 outside 的手续费总量 |
| int256 | feeGrowthOutside1X128 | 以 token1 收取的 outside 的手续费总量 |
| int256 | secondsOutside | 价格在 outside 的总时间 |
| int256 | tickCumulativeOutside | 价格在 outside 的 tick 序号累加 |
| int256 | secondsPerLiquidityOutsideX128 | 价格在 outside 的每单位流动性参与时长 |
tick 辅助预言机的变量的使用方法:
secondsOutside: 用池子创建以来的总时间减去价格区间两边 tick 上的该变量,就能得出该区间做市的总时长tickCumulativeOutside: 用预言机的tickCumulative减去价格区间两边 tick 上的该变量,除以做市时长,就能得出该区间平均的做市价格(tick 序号)secondsPerLiquidityOutsideX128: 用预言机的secondsPerLiquidityCumulative减去价格区间两边 tick 上的该变量,就是该区间内的每单位流动性的做市时长(使用该结果乘以你的流动性数量,得出你的流动性参与的做市时长,这个时长比上 1 的结果,就是你在该区间赚取的手续费比例)。
观测和基数
我们首先创建 Oracle 库,以及 Observation 结构体:
struct Observation {
// the block timestamp of the observation
uint32 blockTimestamp;
// the tick accumulator, i.e. tick * time elapsed since the pool was first initialized
int56 tickCumulative;
// the seconds per liquidity, i.e. seconds elapsed / max(1, liquidity) since the pool was first initialized
uint160 secondsPerLiquidityCumulativeX128;
// whether or not the observation is initialized
bool initialized;
}
tickCumulative
tickCumulative 存储观察时秒数/范围内流动性的值。
该值单调递增,每秒增加秒数/范围内流动性的值。
要得出某个时间间隔内的调和平均流动性,调用者需要依次检索两个观测值,取两个值的差值,然后用经过的时间除以该值。
举例:
tickCumulative as [70_000, 1_070_000]
Time_elapse = 10 s
Average_Tick = (1_070_000 - 70_000)/10 = 100_000
Average_Price = 1.0001 ** i = 1.0001 ** 100_000 ≅ 22015.5
secondsPerLiquidityCumulativeX128
*一个观测(observation)*是存储一个记录价格的 slot。它存储一个价格,记录这个价格时的时间戳,以及一个 initialized 标志位,当这个观测被激活时设置为 true(并不是所有的观测都默认激活)。一个池子合约能够存储至多 65535 个观测:
// src/UniswapV3Pool.sol
contract UniswapV3Pool is IUniswapV3Pool {
using Oracle for Oracle.Observation[65535];
...
Oracle.Observation[65535] public observations;
}
然而,由于存储这么多 Observation 的实例会需要大量的 gas(总有人要为大量合约存储的写操作付款),一个池子默认只存储一个观测,每次新价格记录时都会把它覆盖掉。激活的观测数量,也即观测的基数(cardinality),可以由任何愿意付款的人在任何时间增加。为了管理基数,我们需要一些额外的状态变量:
...
struct Slot0 {
// Current sqrt(P)
uint160 sqrtPriceX96;
// Current tick
int24 tick;
// Most recent observation index
uint16 observationIndex;
// Maximum number of observations
uint16 observationCardinality;
// Next maximum number of observations
uint16 observationCardinalityNext;
}
...
observationIndex记录最新的观测的编号;observationCardinality记录活跃的观测数量;observationCardinalityNext记录观测数组能够扩展到的下一个基数的大小。
观测存储在一个定长的数组里,当一个新的观测被存储并且 observationCardinalityNext 超过 observationCardinality 的时候就会扩展。如果一个数组不能被扩展(下一个基数与现在的基数相同),旧的观测就会被覆盖,例如一个观测存储在下标 0,下一个就存储在下标 1,以此类推。
当池子创建的时候,observationCardinality 和 observationCardinalityNext 都设置为 1:
// src/UniswapV3Pool.sol
contract UniswapV3Pool is IUniswapV3Pool {
function initialize(uint160 sqrtPriceX96) public {
...
(uint16 cardinality, uint16 cardinalityNext) = observations.initialize(
_blockTimestamp()
);
slot0 = Slot0({
sqrtPriceX96: sqrtPriceX96,
tick: tick,
observationIndex: 0,
observationCardinality: cardinality,
observationCardinalityNext: cardinalityNext
});
}
}
// src/lib/Oracle.sol
library Oracle {
...
function initialize(Observation[65535] storage self, uint32 time)
internal
returns (uint16 cardinality, uint16 cardinalityNext)
{
self[0] = Observation({
timestamp: time,
tickCumulative: 0,
initialized: true
});
cardinality = 1;
cardinalityNext = 1;
}
...
}
写入观测
在 swap 函数中,当现价改变时,一个观测会被写入观测数组:
// src/UniswapV3Pool.sol
contract UniswapV3Pool is IUniswapV3Pool {
function swap(...) public returns (...) {
...
if (state.tick != slot0_.tick) {
(
uint16 observationIndex,
uint16 observationCardinality
) = observations.write(
slot0_.observationIndex,
_blockTimestamp(),
slot0_.tick,
slot0_.observationCardinality,
slot0_.observationCardinalityNext
);
(
slot0.sqrtPriceX96,
slot0.tick,
slot0.observationIndex,
slot0.observationCardinality
) = (
state.sqrtPriceX96,
state.tick,
observationIndex,
observationCardinality
);
}
...
}
}
注意到,这里观测的 tick 是 slot0_.tick(而不是 state.tick),也即这笔交易之前的价格!它在下一条语句中更新为新的价格。这正是我们之前讨论到的防价格操控机制:Uniswap 记录这个区块第一笔交易之前的价格,以及上一个区块最后一笔交易之后的价格。
另外要注意到,每个观测都通过 _blockTimestamp() 来标识,也即现在区块的时间戳。这意味着如果现在区块已经存在一个观测了,那么价格将不会被记录。如果当前区块没有观测(也即这是本区快中的第一笔 Uniswap 交易),价格才会被记录。这也是防价格操控机制的一部分。
// src/lib/Oracle.sol
function write(
Observation[65535] storage self,
uint16 index,
uint32 timestamp,
int24 tick,
uint16 cardinality,
uint16 cardinalityNext
) internal returns (uint16 indexUpdated, uint16 cardinalityUpdated) {
Observation memory last = self[index];
if (last.timestamp == timestamp) return (index, cardinality);
if (cardinalityNext > cardinality && index == (cardinality - 1)) {
cardinalityUpdated = cardinalityNext;
} else {
cardinalityUpdated = cardinality;
}
indexUpdated = (index + 1) % cardinalityUpdated;
self[indexUpdated] = transform(last, timestamp, tick);
}
这里我们看到,如当前区块已经存在一个观测,那么将会跳过写。如果现在没有存在这样的观测,我们将会存储一个新的,并且在可能的时候尝试扩展基数。取模运算符(%)确保了观测的下标保持在 $[0, cardinality)$ 区间中,并且当达到上界时重置为 0。
接下来,我们来看一下 transform 函数:
function transform(
Observation memory last,
uint32 timestamp,
int24 tick
) internal pure returns (Observation memory) {
uint56 delta = timestamp - last.timestamp;
return
Observation({
timestamp: timestamp,
tickCumulative: last.tickCumulative +
int56(tick) *
int56(delta),
initialized: true
});
}
在这里,我们计算的是累积价格:现在的 tick 乘以上次观测到现在的秒数,并加到上一个累积价格之上。
增加基数
现在,让我们来看一下基数是如何扩展的。
任何人在任何时间都可以扩展一个池子中观测的基数,并为此支付 gas。因此,我们需要在池子合约中增添一个新的 public 的函数:
// src/UniswapV3Pool.sol
function increaseObservationCardinalityNext(
uint16 observationCardinalityNext
) public {
uint16 observationCardinalityNextOld = slot0.observationCardinalityNext;
uint16 observationCardinalityNextNew = observations.grow(
observationCardinalityNextOld,
observationCardinalityNext
);
if (observationCardinalityNextNew != observationCardinalityNextOld) {
slot0.observationCardinalityNext = observationCardinalityNextNew;
emit IncreaseObservationCardinalityNext(
observationCardinalityNextOld,
observationCardinalityNextNew
);
}
}
以及 Oracle 合约中的一个新函数:
// src/lib/Oracle.sol
function grow(
Observation[65535] storage self,
uint16 current,
uint16 next
) internal returns (uint16) {
if (next <= current) return current;
for (uint16 i = current; i < next; i++) {
self[i].timestamp = 1;
}
return next;
}
在 grow 函数中,我们通过把 timestamp 值设置为一些非零值来分配这些新的观测。注意到,self 是一个 storage 的变量,为它的元素分配值会更新数组计数器,并且把这些值写道合约的存储中。
读取观测
最后我们来到了这章中最棘手的一个部分:读取观测。在开始之前,我们来复习一下观测是如何存储的,以便于我们更好地理解。
观测是存储在一个长度可扩展的定长数组中:
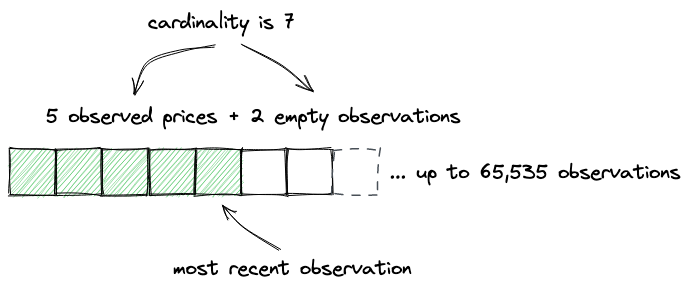
正如我们上面所说,观测是可以溢出的:如果一个新的观测不能直接塞进数组,写操作会重新从下标0开始,也即最老的观测将会被覆盖:
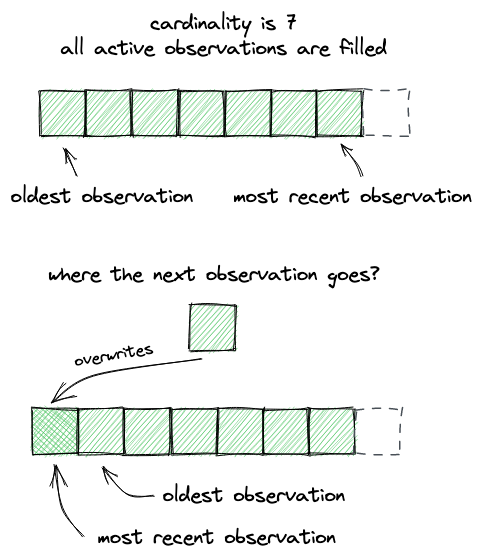
并不是每个区块都保证存在观测,因为交易并不一定在每个区块中都有。因此,会存在一些区块我们不知道价格,并且这样缺失的观测可能会很多。当然,我们并不希望在我们预言机提供的价格之间有很大空缺,这也是我们为什么使用时间加权平均价格(TWAP)——这样我们可以在没有观测的地方使用平均价格。TWAP 让我们能够做价格插值,即在两个观测之间画一条线,每个在这条线上的点都是两个观测之间某个时间戳对应的价格。
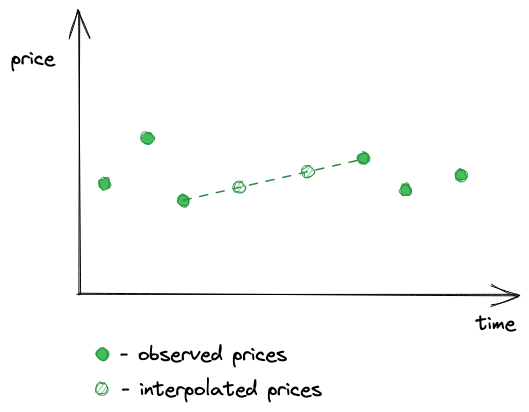
因此,读取观测意味着通过时间戳寻找到观测,并且在确实的观测处插值,同时要考虑到观测数组是可以溢出的(即数组中最老的观测可以在最新的观测之后)。由于我们并不是用时间戳作为下标来索引观测(为了节省 gas),我们需要使用二分查找算法来更有效地查找。但并不总是如此。
让我们来把它拆解成更小的步骤,首先来实现 Oracle 库中的 observe 函数:
function observe(
Observation[65535] storage self,
uint32 time,
uint32[] memory secondsAgos,
int24 tick,
uint16 index,
uint16 cardinality
) internal view returns (int56[] memory tickCumulatives) {
tickCumulatives = new int56[](secondsAgos.length);
for (uint256 i = 0; i < secondsAgos.length; i++) {
tickCumulatives[i] = observeSingle(
self,
time,
secondsAgos[i],
tick,
index,
cardinality
);
}
}
这个函数接受当前区块时间戳,我们希望获取价格的时间点列表(secondsAgo),现在的 tick、观测下标以及基数,作为参数。
接下来看一下 observeSingle 函数:
function observeSingle(
Observation[65535] storage self,
uint32 time,
uint32 secondsAgo,
int24 tick,
uint16 index,
uint16 cardinality
) internal view returns (int56 tickCumulative) {
if (secondsAgo == 0) {
Observation memory last = self[index];
if (last.timestamp != time) last = transform(last, time, tick);
return last.tickCumulative;
}
...
}
在请求观测时,我们需要在二分查找之前进行一些检查:
- 如果请求的时间点是最新的观测,我们可以返回最新观测中的数据;
- 如果请求的时间点是在最新的观测之后,我们可以调用
transform来找到当前时间点上的累积价格(根据最新的观测); - 如果请求的时间点在最新观测之前,我们需要使用二分查找。
上面的代码片段执行了前两点,secondsAgo == 0 即代表请求当前区块的观测。接下来我们来看第三点:
function binarySearch(
Observation[65535] storage self,
uint32 time,
uint32 target,
uint16 index,
uint16 cardinality
)
private
view
returns (Observation memory beforeOrAt, Observation memory atOrAfter)
{
...
这个函数参数为现在的区块时间戳(time),请求价格的时间点(target),以及现在观测的索引和基数。它返回两个观测的区间,请求的时间点就在这个区间之中。
在初始化二分查找过程中,我们设置边界:
uint256 l = (index + 1) % cardinality; // oldest observation
uint256 r = l + cardinality - 1; // newest observation
uint256 i;
记得观测数组是可以溢出的,因此我们上面使用了模运算。
然后我们进入一个循环,每次检查区间的中点:如果它没有初始化(那里没有观测),我们将会进入下一个循环:
while (true) {
i = (l + r) / 2;
beforeOrAt = self[i % cardinality];
if (!beforeOrAt.initialized) {
l = i + 1;
continue;
}
...
如果这个点已初始化,我们把它当做我们请求时间点所在区间的左边界。接下来我们尝试去验证右边界(atOrAfter):
...
atOrAfter = self[(i + 1) % cardinality];
bool targetAtOrAfter = lte(time, beforeOrAt.timestamp, target);
if (targetAtOrAfter && lte(time, target, atOrAfter.timestamp))
break;
...
如果我们已经找到了边界,我们就直接返回。否则我们继续搜索:
...
if (!targetAtOrAfter) r = i - 1;
else l = i + 1;
}
在找到请求时间点所在的观测区间后,我们需要计算请求时间点的价格:
// function observeSingle() {
...
uint56 observationTimeDelta = atOrAfter.timestamp -
beforeOrAt.timestamp;
uint56 targetDelta = target - beforeOrAt.timestamp;
return
beforeOrAt.tickCumulative +
((atOrAfter.tickCumulative - beforeOrAt.tickCumulative) /
int56(observationTimeDelta)) *
int56(targetDelta);
...
这部分很简单,就是求出在这个区间中价格变化的平均速率,乘以从下界到我们需要时间点之间的秒数。这就是我们之前讨论过的插值。
我们最后需要实现的就是池子合约中的一个 public 函数,读取并返回观测:
// src/UniswapV3Pool.sol
function observe(uint32[] calldata secondsAgos)
public
view
returns (int56[] memory tickCumulatives)
{
return
observations.observe(
_blockTimestamp(),
secondsAgos,
slot0.tick,
slot0.observationIndex,
slot0.observationCardinality
);
}
解析观测
现在我们来看一下如何解析观测。
我们刚才实现的 observe 函数返回一个累积价格的数组,现在我们希望把它们转换成真正的价格。我会在 observe 函数的测试中解释如何实现这一点。
在测试中,我在不同区块、不同方向上执行了多笔不同的交易:
function testObserve() public {
...
pool.increaseObservationCardinalityNext(3);
vm.warp(2);
pool.swap(address(this), false, swapAmount, sqrtP(6000), extra);
vm.warp(7);
pool.swap(address(this), true, swapAmount2, sqrtP(4000), extra);
vm.warp(20);
pool.swap(address(this), false, swapAmount, sqrtP(6000), extra);
...
vm.warp是 Foundry 的一个 cheat code:它使用指定的时间戳产生一个新的区块——2,7,20 这些是区块时间戳。
第一笔交易发生在时间戳为2的区块,第二个在时间戳7,第三个在时间戳20。然后我们可以读取这些观测:
...
secondsAgos = new uint32[](4);
secondsAgos[0] = 0;
secondsAgos[1] = 13;
secondsAgos[2] = 17;
secondsAgos[3] = 18;
// 注意这里是secondsAgo,所以用20减去,能对应上面的每个时间戳
int56[] memory tickCumulatives = pool.observe(secondsAgos);
assertEq(tickCumulatives[0], 1607059);
assertEq(tickCumulatives[1], 511146);
assertEq(tickCumulatives[2], 170370);
assertEq(tickCumulatives[3], 85176);
...
- 最早观测的价格是 0,即在池子部署时初始的观测。然而,由于我们设置的基数是 3,我们进行了3笔交易,它被最后一个观测覆盖了。
- 在第一笔交易中,观测到的 tick 是 85176,也即池子的初始价格——回忆一下,我们观测到的是区块中第一笔交易之前的价格。由于最早的一笔观测被覆盖掉了,这实际上是数组中最早的一个观测。
- 下一个返回的累计价格是 170370,也即
85176 + 85194。前者是之前的累积价格,后者是第一笔交易之后的价格,在下一个区块中被观测到。 - 下一个累积价格是 511146,即
(511146 - 170370) / (17 - 13) = 85194,在第二笔交易和第三笔交易之间的累积价格。 - 最后,最新的观测是 1607059,也即
(1607059 - 511146) / (20 - 7) = 84301,约为 4581 USDC/ETH,这事第二笔交易的价格,在第三笔交易中被观测到。
下面是一个包含了插值的测试样例:观测的时间点不是交易发生的时间点:
secondsAgos = new uint32[](5);
secondsAgos[0] = 0;
secondsAgos[1] = 5;
secondsAgos[2] = 10;
secondsAgos[3] = 15;
secondsAgos[4] = 18;
tickCumulatives = pool.observe(secondsAgos);
assertEq(tickCumulatives[0], 1607059);
assertEq(tickCumulatives[1], 1185554);
assertEq(tickCumulatives[2], 764049);
assertEq(tickCumulatives[3], 340758);
assertEq(tickCumulatives[4], 85176);
结果对应的价格分别是:4581.03, 4581.03, 4747.6, 5008.91,即对应间隔的平均价格。
如何在 Python 中计算这些价格:
vals = [1607059, 1185554, 764049, 340758, 85176] secs = [0, 5, 10, 15, 18] [1.0001**((vals[i] - vals[i+1]) / (secs[i+1] - secs[i])) for i in range(len(vals)-1)]
NFT Positions
将学习如何扩展 Uniswap 合约,以及将它集成到第三方的协议中。
Uniswap V3 的一个额外特性是能够把流动性位置转换成 NFT。这是其中一个的例子:
它展示了 token 的信息:
[ positions(uint256) method Response ]
nonce uint96 : 0
operator address : 0x0000000000000000000000000000000000000000
token0 address : 0xB035723D62e0e2ea7499D76355c9D560f13ba404
token1 address : 0xbb4CdB9CBd36B01bD1cBaEBF2De08d9173bc095c
fee uint24 : 10000
tickLower int24 : -96600
tickUpper int24 : -82800
liquidity uint128 : 0
feeGrowthInside0LastX128 uint256 : 19275342891285237278050788030132407641
feeGrowthInside1LastX128 uint256 : 151805030514340226583840194092093
tokensOwed0 uint128 : 0
tokensOwed1 uint128 : 0
]
完整合约代码
NFT 管理员合约
显然,我们并不会把 NFT 相关的功能添加到池子合约中——我们需要一个另外的合约来把 NFT 和流动性位置合并起来。回忆一下,在我们的实现过程中,我们构建了 UniswapV3Manager 来辅助我们与池子合约的交互(使得计算更简单,并能够进行多池子交易)。这个合约向我们展示了一个如何扩展 Uniswap 核心合约的优秀实例。现在,我们将会把这个想法进一步扩展。
我们需要一个管理合约,它实现了 ERC721 标准并且管理流动性位置。这个合约将会有 NFT 标准的功能(铸造、燃烧、转移、余额与所有权跟踪等等),同时也能够向池子添加流动性或者从池子中移除流动性。这个合约应该是池子中流动性的实际拥有者,因为我们不希望让用户不铸造 token 就添加流动性,或者移除了流动性却没有燃烧掉一个 token。我们希望每个流动性位置都与一个 NFT token 链接,并且始终保持同步。
让我们看一下我们需要在新合约中实现的功能:
- 由于这是一个 NFT 合约,它需要有所有的 ERC721 函数,包括
tokenURI,返回一个 NFT 图片的 URI; mint和burn,来同时铸造和燃烧流动性以及 NFT;addLiquidity和removeLiquidity,来在已有的位置上添加和移除流动性;collect,在移除流动性之后收回费用。
让我们开始写代码吧。
最小合约
我们并不希望从零开始实现 ERC721 标准,所以我们使用已有的库。我们依赖中已经有了 Solmate,所以我们会使用它的 ERC721 实现。
使用 OpenZeppelin 的 ERC721 合约也是可以的,不过这里选择使用更省 gas 的 Solmate 版本。
这是一个什么空的的最小的 NFT 管理员合约:
contract UniswapV3NFTManager is ERC721 {
address public immutable factory;
constructor(address factoryAddress)
ERC721("UniswapV3 NFT Positions", "UNIV3")
{
factory = factoryAddress;
}
function tokenURI(uint256 tokenId)
public
view
override
returns (string memory)
{
return "";
}
}
在我们实现元数据和 SVG 渲染器之前,这里的 tokenURI 都会返回一个空字符串。我们添加这个函数以便于我们在实现合约剩余部分的时候,Solidity 编译器不会因此报错(Solmate ERC721 实现中的 tokenURI 函数被声明为 virtual,所以我们必须实现它)。
铸造
正如我们之前所说,铸造会包含两个操作:在池子中添加流动性和铸造一个 NFT。
为了保存池子流动性位置与 NFT 之间的关系,我们需要一个 mapping 以及一个结构体:
struct TokenPosition {
address pool;
int24 lowerTick;
int24 upperTick;
}
mapping(uint256 => TokenPosition) public positions;
找到一个位置我们需要:
- 池子地址
- 所有者地址
- 上下界的 tick
由于 NFT 管理员合约是通过它创建的所有流动性位置的所有者,这部分不需要存储,我们只需要存储剩下两部分数据。positions mapping 里面的键值是 token ID;这个 mapping 把 NFT ID 与找到流动性位置所需要的数据联系在一起。
接下来我们实现铸造:
struct MintParams {
address recipient;
address tokenA;
address tokenB;
uint24 fee;
int24 lowerTick;
int24 upperTick;
uint256 amount0Desired;
uint256 amount1Desired;
uint256 amount0Min;
uint256 amount1Min;
}
function mint(MintParams calldata params) public returns (uint256 tokenId) {
...
}
铸造的参数与 UniswapV3Manager 中的一致,多了一个 recipient,让我们把 NFT 铸造到一个其他地址。
在 mint 函数中,我们首先向池子中添加流动性:
IUniswapV3Pool pool = getPool(params.tokenA, params.tokenB, params.fee);
(uint128 liquidity, uint256 amount0, uint256 amount1) = _addLiquidity(
AddLiquidityInternalParams({
pool: pool,
lowerTick: params.lowerTick,
upperTick: params.upperTick,
amount0Desired: params.amount0Desired,
amount1Desired: params.amount1Desired,
amount0Min: params.amount0Min,
amount1Min: params.amount1Min
})
);
_addLiquidity 与 UniswapV3Manager 中 mint 函数的部分一致:把 tick 转换成 $\sqrt(P)$,计算流动性数量,然后调用 pool.mint()。
接下来,我们铸造一个 NFT:
tokenId = nextTokenId++;
_mint(params.recipient, tokenId);
totalSupply++;
tokenId 设置为现在的 nextTokenId,然后后者自增。_mint 函数是 Solmate 的 ERC721 合约提供的。在铸造一个新的 token 之后,我们更新 totalSupply。
最后,我们需要把新的 token 和新的流动性位置信息存储下来:
TokenPosition memory tokenPosition = TokenPosition({
pool: address(pool),
lowerTick: params.lowerTick,
upperTick: params.upperTick
});
positions[tokenId] = tokenPosition;
这让我们后续可以通过 token ID 来找到流动性位置。
添加流动性
接下来,我们将实现一个函数,把流动性添加到已有的位置中。当我们希望我们已经提供过流动性的某个位置拥有更多流动性时我们可以调用。在这种情况下,我们并不会铸造一个新的 NFT,而只是增加一个已有位置中流动性的数量。在这里,我们仅需要提供 NFT token ID 和 要添加的 token 数量:
function addLiquidity(AddLiquidityParams calldata params)
public
returns (
uint128 liquidity,
uint256 amount0,
uint256 amount1
)
{
TokenPosition memory tokenPosition = positions[params.tokenId];
if (tokenPosition.pool == address(0x00)) revert WrongToken();
(liquidity, amount0, amount1) = _addLiquidity(
AddLiquidityInternalParams({
pool: IUniswapV3Pool(tokenPosition.pool),
lowerTick: tokenPosition.lowerTick,
upperTick: tokenPosition.upperTick,
amount0Desired: params.amount0Desired,
amount1Desired: params.amount1Desired,
amount0Min: params.amount0Min,
amount1Min: params.amount1Min
})
);
}
这个函数确保了已经存在一个这样的 token,并且使用对应 position 的参数来调用 pool.mint()。
移除流动性
我们在 UniswapV3Manager 合约中并没有实现 burn 函数,因为我们希望用户作为流动性位置的所有者。现在,流动性所有者是这个 NFT 管理员合约,我们可以这样来实现燃烧流动性:
struct RemoveLiquidityParams {
uint256 tokenId;
uint128 liquidity;
}
function removeLiquidity(RemoveLiquidityParams memory params)
public
isApprovedOrOwner(params.tokenId)
returns (uint256 amount0, uint256 amount1)
{
TokenPosition memory tokenPosition = positions[params.tokenId];
if (tokenPosition.pool == address(0x00)) revert WrongToken();
IUniswapV3Pool pool = IUniswapV3Pool(tokenPosition.pool);
(uint128 availableLiquidity, , , , ) = pool.positions(
poolPositionKey(tokenPosition)
);
if (params.liquidity > availableLiquidity) revert NotEnoughLiquidity();
(amount0, amount1) = pool.burn(
tokenPosition.lowerTick,
tokenPosition.upperTick,
params.liquidity
);
}
我们同样检查 token ID 是否合法。同时,我们也需要确保位置有足够的流动性来燃烧。
收集 Token
NFT 管理员合约也可以在燃烧流动性之后收集 token。注意到,收集的 token 发送给了 msg.sender,因为这个合约代替用户管理了流动性:
struct CollectParams {
uint256 tokenId;
uint128 amount0;
uint128 amount1;
}
function collect(CollectParams memory params)
public
isApprovedOrOwner(params.tokenId)
returns (uint128 amount0, uint128 amount1)
{
TokenPosition memory tokenPosition = positions[params.tokenId];
if (tokenPosition.pool == address(0x00)) revert WrongToken();
IUniswapV3Pool pool = IUniswapV3Pool(tokenPosition.pool);
(amount0, amount1) = pool.collect(
msg.sender,
tokenPosition.lowerTick,
tokenPosition.upperTick,
params.amount0,
params.amount1
);
}
燃烧
最后是燃烧。与这个合约中其他的函数不同,这个函数并不会对池子进行任何操作:它仅仅燃烧一个 NFT。为了燃烧,对应的位置必须是空的并且 token 已经被收集。因此,如果我们想要燃烧一个 NFT,我们需要:
- 调用
removeLiquidity来移除整个区间流动性; - 调用
collect来收集移除流动性获得的 token; - 调用
burn来燃烧这个 NFT token。
function burn(uint256 tokenId) public isApprovedOrOwner(tokenId) {
TokenPosition memory tokenPosition = positions[tokenId];
if (tokenPosition.pool == address(0x00)) revert WrongToken();
IUniswapV3Pool pool = IUniswapV3Pool(tokenPosition.pool);
(uint128 liquidity, , , uint128 tokensOwed0, uint128 tokensOwed1) = pool
.positions(poolPositionKey(tokenPosition));
if (liquidity > 0 || tokensOwed0 > 0 || tokensOwed1 > 0)
revert PositionNotCleared();
delete positions[tokenId];
_burn(tokenId);
totalSupply--;
}
完成了!
NFT 渲染器
现在,我们需要构建一个 NFT 渲染器:一个处理 NFT 管理员合约中调用 tokenURI 的库。它会对于每个已经铸造的 token 渲染 JSON 元数据和一个 SVG。正如我们之前所说,我们需要使用 data URI 格式,它要求 base64 编码格式——这意味着我们需要在 Solidity 中的 base64 编码器。但首先,让我们先来看一下我们的 token 长什么样。
SVG 模板
我构建了 Uniswap V3 NFT 的这样一个简化版本:
它的代码如下:
<svg xmlns="http://www.w3.org/2000/svg" viewBox="0 0 300 480">
<style>
.tokens {
font: bold 30px sans-serif;
}
.fee {
font: normal 26px sans-serif;
}
.tick {
font: normal 18px sans-serif;
}
</style>
<rect width="300" height="480" fill="hsl(330,40%,40%)" />
<rect x="30" y="30" width="240" height="420" rx="15" ry="15" fill="hsl(330,90%,50%)" stroke="#000" />
<rect x="30" y="87" width="240" height="42" />
<text x="39" y="120" class="tokens" fill="#fff">
WETH/USDC
</text>
<rect x="30" y="132" width="240" height="30" />
<text x="39" y="120" dy="36" class="fee" fill="#fff">
0.05%
</text>
<rect x="30" y="342" width="240" height="24" />
<text x="39" y="360" class="tick" fill="#fff">
Lower tick: 123456
</text>
<rect x="30" y="372" width="240" height="24" />
<text x="39" y="360" dy="30" class="tick" fill="#fff">
Upper tick: 123456
</text>
</svg>
这是一个简单的 SVG 模板,我们将会实现一个 Solidity 合约来填充这个模板中的一些域并且把它在 tokenURI 中返回。以下这些与是在每个 token 中不同的:
- 背景颜色,在最开始的两个
rect中进行设置;色调(hue)属性(在模板中为 330)对每个 token 是不同的; - 对应流动性位置属于的池子的名字(模板中为 WETH/USDC);
- 池子费率(0.05%);
- 区间边界的 tick 值(123456)。
下面是两个我们合约会产生的 NFT 的例子:


依赖
Solidity 并没有提供原生的 base64 编码工具,所以我们需要使用第三方库。在这里,我们使用 OpenZeppelin 的库。
另一个麻烦的事情是 Solidity 对于字符串操作的支持非常匮乏。例如,我们没办法把整数穿换成字符串——但是我们在这里需要把池子费率和 tick 值渲染进 SVG 模板里面。我们会使用 OpenZeppelin 的 Strings 库来实现。
结果格式
渲染器输出的格式应该是如下这样:
data:application/json;base64,BASE64_ENCODED_JSON
JSON 文件会长这样:
{
"name": "Uniswap V3 Position",
"description": "USDC/DAI 0.05%, Lower tick: -520, Upper text: 490",
"image": "BASE64_ENCODED_SVG"
}
“image” 域的内容会是上面填充后的 SVG 模板并用 base64 编码后的结果。
实现渲染器
我们将会在一个额外的库合约中实现渲染器,防止 NFT 管理员合约变得太过复杂:
library NFTRenderer {
struct RenderParams {
address pool;
address owner;
int24 lowerTick;
int24 upperTick;
uint24 fee;
}
function render(RenderParams memory params) {
...
}
}
在 render 函数中,我们首先渲染一个 SVG,然后是一个 JSON。为了让代码更简洁,我们会把每一步分解成更小的步骤。
首先获取 token 的标识:
function render(RenderParams memory params) {
IUniswapV3Pool pool = IUniswapV3Pool(params.pool);
IERC20 token0 = IERC20(pool.token0());
IERC20 token1 = IERC20(pool.token1());
string memory symbol0 = token0.symbol();
string memory symbol1 = token1.symbol();
...
SVG 渲染
接下来我们就可以渲染 SVG 模板了:
string memory image = string.concat(
"<svg xmlns='http://www.w3.org/2000/svg' viewBox='0 0 300 480'>",
"<style>.tokens { font: bold 30px sans-serif; }",
".fee { font: normal 26px sans-serif; }",
".tick { font: normal 18px sans-serif; }</style>",
renderBackground(params.owner, params.lowerTick, params.upperTick),
renderTop(symbol0, symbol1, params.fee),
renderBottom(params.lowerTick, params.upperTick),
"</svg>"
);
这个模板被分成了好多部分:
- 首先是 header,包含 CSS 样式;
- 然后渲染背景;
- 然后渲染位置信息(token 标识和费率);
- 最后渲染底部信息(位置边界 tick)。
背景就是两个 rect。为了渲染背景,我们需要求出这个 token 对应的唯一的 hue。然后我们把所有的部分拼起来:
function renderBackground(
address owner,
int24 lowerTick,
int24 upperTick
) internal pure returns (string memory background) {
bytes32 key = keccak256(abi.encodePacked(owner, lowerTick, upperTick));
uint256 hue = uint256(key) % 360;
background = string.concat(
'<rect width="300" height="480" fill="hsl(',
Strings.toString(hue),
',40%,40%)"/>',
'<rect x="30" y="30" width="240" height="420" rx="15" ry="15" fill="hsl(',
Strings.toString(hue),
',100%,50%)" stroke="#000"/>'
);
}
顶部模板渲染 token 标识和池子费率:
function renderTop(
string memory symbol0,
string memory symbol1,
uint24 fee
) internal pure returns (string memory top) {
top = string.concat(
'<rect x="30" y="87" width="240" height="42"/>',
'<text x="39" y="120" class="tokens" fill="#fff">',
symbol0,
"/",
symbol1,
"</text>"
'<rect x="30" y="132" width="240" height="30"/>',
'<text x="39" y="120" dy="36" class="fee" fill="#fff">',
feeToText(fee),
"</text>"
);
}
费率渲染为一个小数。由于我们预先知道了所有可能的费率,我们并不需要把整数转换成小数,只需要硬编码即可:
function feeToText(uint256 fee)
internal
pure
returns (string memory feeString)
{
if (fee == 500) {
feeString = "0.05%";
} else if (fee == 3000) {
feeString = "0.3%";
}
}
在底部我们渲染区间的 tick:
function renderBottom(int24 lowerTick, int24 upperTick)
internal
pure
returns (string memory bottom)
{
bottom = string.concat(
'<rect x="30" y="342" width="240" height="24"/>',
'<text x="39" y="360" class="tick" fill="#fff">Lower tick: ',
tickToText(lowerTick),
"</text>",
'<rect x="30" y="372" width="240" height="24"/>',
'<text x="39" y="360" dy="30" class="tick" fill="#fff">Upper tick: ',
tickToText(upperTick),
"</text>"
);
}
由于 tick 可能为正可能为负,我们需要正确渲染它们(带不带负号):
function tickToText(int24 tick)
internal
pure
returns (string memory tickString)
{
tickString = string.concat(
tick < 0 ? "-" : "",
tick < 0
? Strings.toString(uint256(uint24(-tick)))
: Strings.toString(uint256(uint24(tick)))
);
}
JSON 渲染
现在,让我们回到 render 函数,来渲染 JSON。首先,我们需要渲染一个 token 描述:
function render(RenderParams memory params) {
... SVG rendering ...
string memory description = renderDescription(
symbol0,
symbol1,
params.fee,
params.lowerTick,
params.upperTick
);
...
token 描述是一个文本字符串,包含了我们在 token SVG 中所有相同的信息:
function renderDescription(
string memory symbol0,
string memory symbol1,
uint24 fee,
int24 lowerTick,
int24 upperTick
) internal pure returns (string memory description) {
description = string.concat(
symbol0,
"/",
symbol1,
" ",
feeToText(fee),
", Lower tick: ",
tickToText(lowerTick),
", Upper text: ",
tickToText(upperTick)
);
}
现在我们可以开始组装 JSON 元数据了:
function render(RenderParams memory params) {
string memory image = ...SVG rendering...
string memory description = ...description rendering...
string memory json = string.concat(
'{"name":"Uniswap V3 Position",',
'"description":"',
description,
'",',
'"image":"data:image/svg+xml;base64,',
Base64.encode(bytes(image)),
'"}'
);
最后,返回这个结果:
return
string.concat(
"data:application/json;base64,",
Base64.encode(bytes(json))
);
填充 tokenURI
现在,我们可以返回 NFT 管理员合约中的 tokenURI 函数,添加真正的渲染:
function tokenURI(uint256 tokenId)
public
view
override
returns (string memory)
{
TokenPosition memory tokenPosition = positions[tokenId];
if (tokenPosition.pool == address(0x00)) revert WrongToken();
IUniswapV3Pool pool = IUniswapV3Pool(tokenPosition.pool);
return
NFTRenderer.render(
NFTRenderer.RenderParams({
pool: tokenPosition.pool,
owner: address(this),
lowerTick: tokenPosition.lowerTick,
upperTick: tokenPosition.upperTick,
fee: pool.fee()
})
);
}
Gas 花销
尽管有很多优势,在链上存储数据有一个严重的缺点:合约的部署会非常昂贵。在部署合约时,你会按照合约的大小来付费,而这里所有的字符串和模板都会显著增加 gas 开销。而当你的 SVG 越高级:拥有更多的形状,CSS 样式,动画等等,费用就会越昂贵。
我们上面实现的 NFT 渲染器并没有做 gas 优化,你可以看到在字符串中有大量重复的 rect 和 text 这种标签,而我们可以通过内部函数来防止多份存储。我牺牲了 gas 效率来保证合约的可读性比较好。在真正的数据存储在链上的 NFT 项目中,代码的可读性通常会非常的差,因为 gas 优化程度很高。
测试
最后一件事就是我们如何测试 NFT 图像。对 NFT 图像的所有改变都必须被追踪,来保证没有破坏渲染的地方。为了实现这点,我们需要测试 tokenURI 以及它的不同变种的输出(我们甚至可以预渲染出整个集合的图像然后测试,来确保部署后没有图片会出现问题)。
为了测试 tokenURI 的输出,我添加了这个断言函数:
assertTokenURI(
nft.tokenURI(tokenId0),
"tokenuri0",
"invalid token URI"
);
第一个参数是实际的输出,第二个参数是期望值所存储的文件名。这个锻压你会加载文件中的内容,并且与实际返回值相比较:
function assertTokenURI(
string memory actual,
string memory expectedFixture,
string memory errMessage
) internal {
string memory expected = vm.readFile(
string.concat("./test/fixtures/", expectedFixture)
);
assertEq(actual, string(expected), errMessage);
}
多亏了 forge-std 库提供的 vm.readFile() cheatcode 我们才能够在 Solidity 中实现它。这不仅仅更加简单方便,而且也更安全:我们可以配置文件系统的权限,仅允许被许可的文件操作。为了让上述测试能够运行,我们需要在 foundry.toml 中添加这条 fs_permissions 规则:
fs_permissions = [{access='read',path='.'}]
用下面的方法你可以读一个 SVG:
$ cat test/fixtures/tokenuri0 \
| awk -F ',' '{print $2}' \
| base64 -d - \
| jq -r .image \
| awk -F ',' '{print $2}' \
| base64 -d - > nft.svg \
&& open nft.svg
确保你安装了 jq。