恒定函数做市商 (Constant Function Market Makers)
本章节主要讲述了 Uniswap 白皮书中的内容. 理解其中的数学原理能帮助你更好地构建像 Uniswap 这样的应用
正如我们在上一节中提到的那样,AMM 的构建有许多不同的方法。我们将主要关注与构建一种特定的 AMM:恒定函数做市商(有时也被称为恒定乘积做市商)。尽管名字听起来很复杂,但是它的核心数学原理只是一个非常简单的公式:
$$x * y = k$$
仅此而已,这就是 AMM.
$x$ 和 $y$ 是池子合约所拥有的两种资产的数目。$k$ 是它们的乘积,我们暂时不考虑它的实际值等于多少。
为什么只有两种资产x和y? 每个 Uniswap 的池子仅包含两种 资产。我们使用 x 和 y 来表示一个池子中的两种资产,其中 x 代表第一个 token,y 代表第二个 token。两种 token 的顺序(暂时)并不重要。
恒定函数做市商的原理是:在每次 swap 交易后,k 必须保持增加或不变。当用户进行交易,他们通常将一种类型的 token 放入池子(也即他们打算卖出的 token ),并且将另一种类型的 token 移出池子(也即打算购买的 token)。这笔交易会改变池子中两种资产的数量,而上述原理表示,两种资产数目的乘积必须保持不变。我们之后还会在本书中看到许多次这个原理,这就是 Uniswap 的核心机制。
AMM 自动做市商合约内部持有交易对,允许交易对代币之间互相兑换,需要注意的是每次交易兑换都会收取相应的手续费,因此,每笔交易都会推高 k 值:
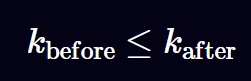
展开上面的方程,我们得到下面的等效方程:
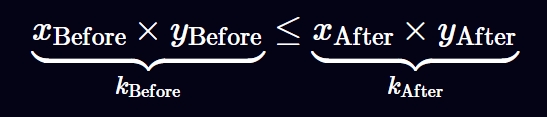
下面我们来看一个更加具体的例子:
- 起始价格为
50(10 ETH = 500 OMG), - 我们卖出
1个ETH,手续费收取 3 % - 如果我们仅以现货价格计算,计算能够获得的
OMG
- 往池子中注入的ETH数量为:
1 *(1-3%) - 注入 ETH 后,池子的ETH代币数量为:
10 + 1*(1-3%) - 10 * 500 <= (10 + 1*(1-3%))* (500 - dy)
- dy <= 44.21,交易实际发生的价格是
44.21
- 交易完成后:
- 交易池子中新增
1 ETH, 总量为10 + 1 = 11 ETH - 交易池子中减少
44.21 OMG,总量为500 - 44.21 = 455.79 OMG - 兑换后后池子总流动性为:
11 * 455.79 = 5013.69 > 5000
因此,由于收续费的原因,每次兑换都会推高总流动性的值,早期提供流动性代币的用户就会获利
交易函数
现在我们知道了什么是池子以及交易的原理,接下来我们写一下交易发生时的公式:
(x + r $\Delta x$)(y - $\Delta y$) >= k, r表示手续费
- 一个池子包含一定数量的
token0($x$) 和一定数量的token1($y$) - 当我们用
token0购买token1的时候,一些token0被放入池子 ($\Delta x$) - 这个池子将给我们一定数量的
token1作为交换 ($\Delta y$) - 池子也会从我们给出的
token0中收取一定数量的手续费 ($r$) - 池子中
token0的数量发生了变化 ($x + r \Delta x$),token1的数量也发生了变化 ($y - \Delta y$) - 二者的乘积保持 >= $k$
我们使用 token0 和 token1 这样的表述,是为了与代码保持一致。现在,两个 token 的顺序并不重要。
简单来说,我们给了池子一定数量的 token0,然后获得了一定数量的 token1。这个池子的工作就是按照一个合理的价格,给予我们正确数量的 token1。我们可以得出以下结论:池子决定了交易的价格。
价格
池子里 token 的价格是如何计算的?
由于 Uniswap 不同的池子对应不同的智能合约,同一个池子里的两种 token 互为计价标准进行定价。例如:在一个 ETH/USDC 的池子里,ETH 的价格用 USDC 作为标定,而 USDC 的价格用 ETH 作为标定。假设一个 ETH 的价格是1000 USDC,那么一个 USDC 的价格就是 0.001 ETH。每一个池子都是如此,无论 token 是否为稳定币(例如,ETH/BTC 池)
在现实世界中,价格是根据供求关系来决定的,对于 AMM 当然也是如此,现在,我们先不考虑需求方,只关注供给方。
池子中 token 的价格是由 token 的供给量决定的,也即池子中拥有该 token 的资产数目。token 的价格公式如下:
$$P_x = \frac{y}{x}, \quad P_y=\frac{x}{y}$$
其中 $P_x$ 和 $P_y$ 是一个 token 相对于另一个 token 的价格
这个价格被称作 现货价格/现价, 它反映了当前的市场价。然而,交易实际成交的价格却并不是这个价格。现在我们再重新把需求方纳入考虑:
根据供求关系,需求越高,价格越高,这也是我们应当在去中心化交易中满足的性质。我们希望当需求很高的时候价格会升高,并且我们能够用池子里的资产数量来衡量需求:你希望从池子中获取某个token的数量越多,价格变动就越剧烈。我们再重新考虑上面这个公式:
(x + r $\Delta x$)(y - $\Delta y$) = xy
从这个公式中,我们能够推导出关于 $\Delta x$ 和 $\Delta y$ 的式子,这也意味着我们能够通过交易付出的 token 数目来计算出获得的 token 数目,反之亦然:
$$\Delta y = \frac{y r \Delta x}{x + r \Delta x}$$ $$\Delta x = \frac{x \Delta y}{r(y - \Delta y)}$$
这些公式就能够让我们重新计算价格。我们能够从 $\Delta y$ 公式中求出获得 token 数量(当我们希望卖出 token 的数量为定值),并且从 $\Delta x$ 的公式中求出需要提供的 token 数量(当我们购买 token 的数量为定值)。注意到,这里的公式是资产之间的关系,同时也把交易的数量(第一个公式中的 $\Delta x$ 和第二个公式中的 $\Delta y$)加入了计算。这是同时考虑了供求双方的价格函数。事实上,我们甚至并不需要去计算价格!(因为我们直接计算出了交易的结果)
下面是从交易函数推导出上述价格函数的过程: $$(x + r\Delta x)(y - \Delta y) = xy$$
$$y - \Delta y = \frac{xy}{x + r\Delta x}$$
$$-\Delta y = \frac{xy}{x + r\Delta x} - y$$
$$-\Delta y = \frac{xy - y({x + r\Delta x})}{x + r\Delta x}$$
$$-\Delta y = \frac{xy - xy - y r \Delta x}{x + r\Delta x}$$
$$-\Delta y = \frac{- y r \Delta x}{x + r\Delta x}$$
$$\Delta y = \frac{y r \Delta x}{x + r\Delta x}$$ 以及: $$(x + r\Delta x)(y - \Delta y) = xy$$
$$x + r\Delta x = \frac{xy}{y - \Delta y}$$
$$r\Delta x = \frac{xy}{y - \Delta y} - x$$
$$r\Delta x = \frac{xy - x(y - \Delta y)}{y - \Delta y}$$
$$r\Delta x = \frac{xy - xy + x \Delta y}{y - \Delta y}$$
$$r\Delta x = \frac{x \Delta y}{y - \Delta y}$$
$$\Delta x = \frac{x \Delta y}{r(y - \Delta y)}$$
曲线
上面的数学计算可能有些抽象和枯燥,下面我们来把恒定乘积函数进行可视化来更好地理解其工作原理
恒定成绩函数的图像为二次双曲线:

横纵轴分别表示池子中两种代币的数量。每一笔交易的起始点都是曲线上与当前两种代币比例相对应的点。为了计算交易获得的 token 数量,我们需要找到曲线上的一个新的点,其横坐标值为 $x+\Delta x$,也即池子中现在 token0 的数量加上我们卖出的数量。y 轴上的变化量就是我们将会获得的 token1 的数量。
下面我们来看一个更加具体的例子:
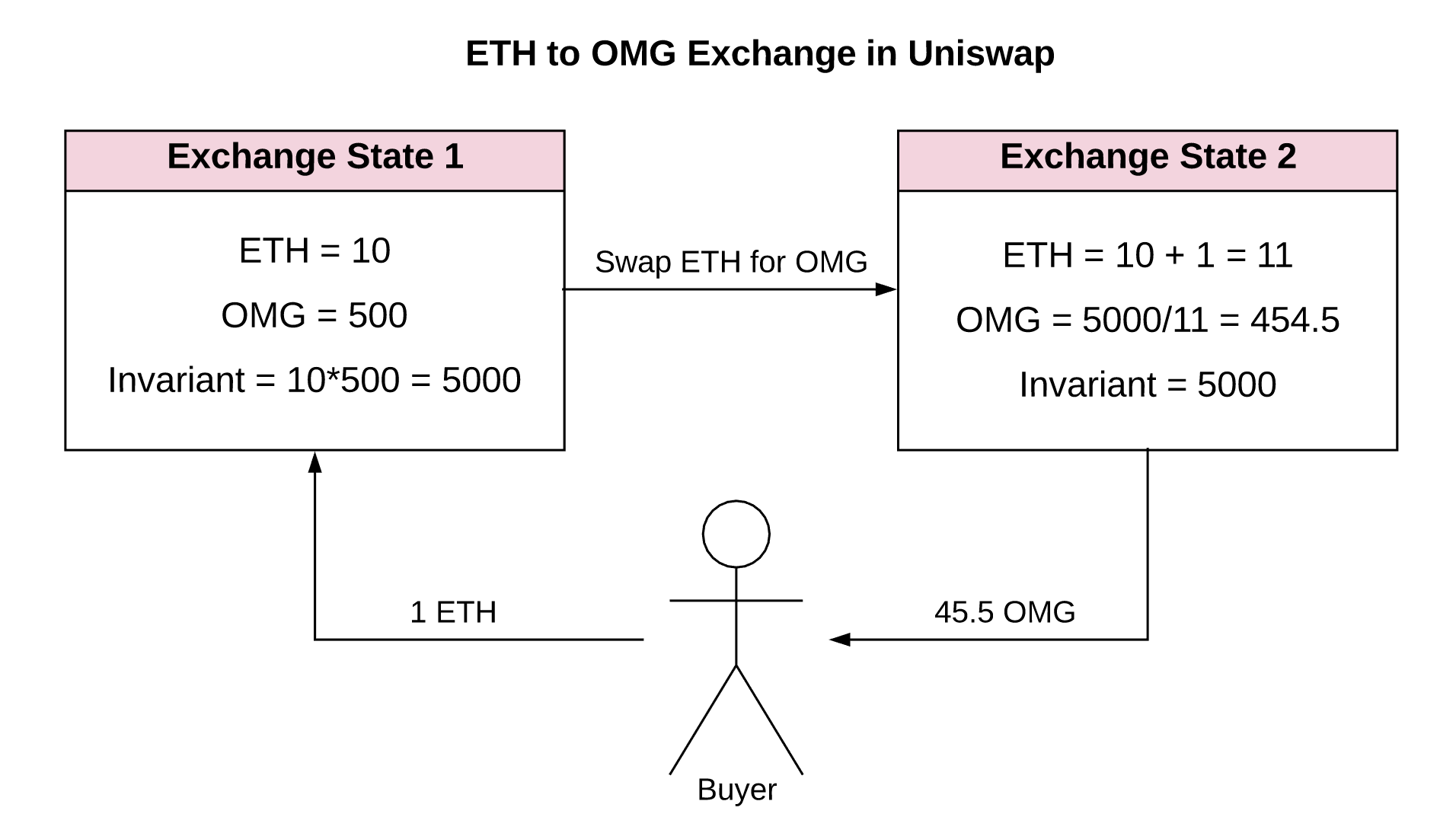
- 紫色的线是公式代表的双曲线,横纵坐标轴代表池子中代币资产的数目(注意到在一开始,两种代币的数量相等)
- 起始价格为
50(1 ETH = 50 OMG) - 我们卖出
1个ETH,如果我们仅以现货价格计算,我们希望获得50个OMG。 - 然而,交易实际发生的价格是
45.5,所以我们仅仅获得了45.5个OMG!
这个例子来源于the Desmos chart,作者是Dan Robinson,
Uniswap 的创始人之一。 为了能够更直观地理解它是如何工作的,你可以尝试自己构建不同的场景并且在图上画出来。试一试不同的资产数目,观察当 $\Delta x$ 远小于 $x$ 时获得代币的数量。
一个很传奇的故事是,Uniswap 就是在 Desmos 中发明出来的.
你或许在想,为什么要用这样的一个曲线?这个曲线看起来好像是在惩罚大额交易者。事实上,的确就是如此,并且这也是一个非常好的性质!供求关系告诉我们,当需求很高的时候(假设供给保持不变),价格也同样很高;当需求低的时候,价格也仍然很低。这正是市场的工作原理。并且很神奇地是,这样一个恒定乘积函数恰好实现了这个机制!需求就是你希望购买 token 的数量,而供给就是池子中的资产。当你希望购买的数量占池子的一个很大比例,价格就会比你购买小数量时更高。这样一个简单的公式,恰恰保证了这么一个强大的机制。
尽管 Uniswap 并不计算交易价格,我们仍然能够从曲线上看到它。事实上,在一笔交易中我们有很多个价格:
- 在交易前,有一个现货价格。这个价格等于池子中两种资产的比例,$y/x$ 或者 $x/y$,取决于你交易的方向。这个价格也是起始点切线的斜率。
- 在交易后,有一个新的现货价格,在曲线上另一个不同的点。这个价格是新的点的切线斜率。
- 这个交易的实际发生价格,是连接新旧点的这条线的斜率。
这就是 UniswapV1/V2 里用到的全部数学!