价格预言机

要在 DEX 中添加的最后一个机制就是价格预言机。

什么是价格预言机？

价格预言机 Oracle 是向区块链提供资产价格的一种机制。

Uniswap V2 Oracle

UniswapV2 需要用户自己实现价格累计的功能合约

    function snapshot(IUniswapV2Pair uniswapV2pair) public {
        require(getTimeElapsed() >= 1 hours, "snapshot is not stale");

        // we don't use the reserves, just need the last timestamp update
        (, , lastSnapshotTime) = uniswapV2pair.getReserves();
        snapshotPrice0Cumulative = uniswapV2pair.price0CumulativeLast();
    }

V2 中跟踪累积价格，也即这个池子合约历史中每秒的价格之和。

$$a_{i} = \sum_{i=1}^t p_{i}$$

这个方法让我们能够找到两个时间点($t_1$ 和 $t_2$)之间的时间加权平均价格(TWAP)，只需要将这两个时间点的累积价格($a_{t_1}$ 和 $a_{t_2}$)相减，除以他们之间相隔的秒数即可：

$$p_{t_1,t_2} = \frac{a_{t_2} - a_{t_1}}{t_2 - t_1}$$

Uniswap V3 oracle

Core Accumulator checkpoints

Uniswap v3 pool 中记录以观测值数组的形式存储。

最初，每个 pool 仅跟踪单个观测值，并随着区块的生成进行覆盖。

这限制了用户可以访问过去数据的时间。

但是，任何愿意支付交易费的一方都可以增加跟踪观测值的数量（最多为65535），从而将数据可用时间延长至约 9 天或更长时间。

将价格和流动性历史记录直接存储在池合约中，可以大大降低调用合约出现逻辑错误的可能性，并通过消除存储历史值的需要来降低集成成本。此外，v3 预言机的最大长度相当大，这使得预言机价格操纵变得更加困难，因为调用合约可以低成本地在预言机数组长度以内（或完全包含）的任意范围内构建时间加权平均值。

在 V3 中，略有一些不同。累积的价格通过 tick 来计算的（也即价格的 $log_{1.0001}$）：

$$a_{i} = \sum_{i=1}^t log_{1.0001}P(i)$$

这里的 log 数值后面其实还有一个 * 1s 即以每秒作为时间间隔。

然而实际情况中，合约中是以区块的时间戳作为标记时间的，所以合约中的代码跟公式不同。

每个区块的头一笔交易时更新，此时距离上一次更新时间间隔肯定大于 1s，所以需要将更新值乘以两个区块的时间戳的差。

tickCumulative 是 tick 序号的累计值，tick 的序号就是 log(√price, 1.0001)。

tickCumulative += tick_current * delta_time
tickCumulative += tick_current * (blocktimestamp_current - blocktimestamp_before)

当外部用户使用时，求 t1 到 t2 时间内的时间加权价格 p(t1,t2) ，需要计算两个时间点的累计值的差 a(t2) - a(t1) 除以时间差。 $$ a_{t2}-a_{t1} = \frac{\sum_{i=t1}^{t2}log_{1.0001}(p_i)}{t2-t1} $$

$$ log_{1.0001}(p_{t1,t2}) = \frac{a_{t2}-a_{t1}}{t2-t1} $$

$$ p_{t1,t2} = {1.0001}^\frac{a_{t2}-a_{t1}}{t2-t1} $$

使用几何平均的原因：

因为合约中记录了 tick 序号，序号是整型，且跟价格相关，所以直接计算序号更加节省 gas。（全局变量中存储的不是价格，而是根号价格，如果直接用价格来记录，要多比较复杂的计算）
V2 中算数平均价格并不总是倒数关系（以 token1 计价 token0，或反过来），所以需要记录两种价格。V3 中使用几何平均不存在该问题，只需要记录一种价格。
- 举个例子，在 V2 中如果 USD/ETH 价格在区块 1 中是 100，在区块 2 中是 300，USD/ETH 的均价是 200 USD/ETH，但是 ETH/USD 的均价是 1/150
几何平均比算数平均能更好的反应真实的价格，受短期波动影响更小。白皮书中的引用提到在几何布朗运动中，算数平均会受到高价格的影响更多。

Tick 上辅助预言机计算的数据

每个已初始化的 tick 上（有流动性添加的），不光有流动性数量和手续费相关的变量(liquidityNet, liquidityGross, feeGrowthOutside)，还有三个可用于做市策略。

tick 变量一览：

Type	Variable Name	含义
int128	liquidityNet	流动性数量净含量
int128	liquidityGross	流动性数量总量
int256	feeGrowthOutside0X128	以 token0 收取的 outside 的手续费总量
int256	feeGrowthOutside1X128	以 token1 收取的 outside 的手续费总量
int256	secondsOutside	价格在 outside 的总时间
int256	tickCumulativeOutside	价格在 outside 的 tick 序号累加
int256	secondsPerLiquidityOutsideX128	价格在 outside 的每单位流动性参与时长

tick 辅助预言机的变量的使用方法：

secondsOutside：用池子创建以来的总时间减去价格区间两边 tick 上的该变量，就能得出该区间做市的总时长
tickCumulativeOutside：用预言机的 tickCumulative 减去价格区间两边 tick 上的该变量，除以做市时长，就能得出该区间平均的做市价格（tick 序号）
secondsPerLiquidityOutsideX128：用预言机的 secondsPerLiquidityCumulative 减去价格区间两边 tick 上的该变量，就是该区间内的每单位流动性的做市时长（使用该结果乘以你的流动性数量，得出你的流动性参与的做市时长，这个时长比上 1 的结果，就是你在该区间赚取的手续费比例）。

观测和基数

我们首先创建 Oracle 库，以及 Observation 结构体：

struct Observation {
  // the block timestamp of the observation
  uint32 blockTimestamp;
  // the tick accumulator, i.e. tick * time elapsed since the pool was first initialized
  int56 tickCumulative;
  // the seconds per liquidity, i.e. seconds elapsed / max(1, liquidity) since the pool was first initialized
  uint160 secondsPerLiquidityCumulativeX128;
  // whether or not the observation is initialized
  bool initialized;
}

tickCumulative

tickCumulative 存储观察时秒数/范围内流动性的值。该值单调递增，每秒增加秒数/范围内流动性的值。

要得出某个时间间隔内的调和平均流动性，调用者需要依次检索两个观测值，取两个值的差值，然后用经过的时间除以该值。

举例：

tickCumulative as [70_000, 1_070_000]

Time_elapse = 10 s

Average_Tick = (1_070_000 - 70_000)/10 = 100_000

Average_Price = 1.0001 ** i = 1.0001 ** 100_000 ≅ 22015.5

secondsPerLiquidityCumulativeX128

*一个观测(observation)*是存储一个记录价格的 slot。它存储一个价格，记录这个价格时的时间戳，以及一个 initialized 标志位，当这个观测被激活时设置为 true（并不是所有的观测都默认激活）。一个池子合约能够存储至多 65535 个观测：

// src/UniswapV3Pool.sol
contract UniswapV3Pool is IUniswapV3Pool {
    using Oracle for Oracle.Observation[65535];
    ...
    Oracle.Observation[65535] public observations;
}

然而，由于存储这么多 Observation 的实例会需要大量的 gas（总有人要为大量合约存储的写操作付款），一个池子默认只存储一个观测，每次新价格记录时都会把它覆盖掉。激活的观测数量，也即观测的基数(cardinality)，可以由任何愿意付款的人在任何时间增加。为了管理基数，我们需要一些额外的状态变量：

    ...
    struct Slot0 {
        // Current sqrt(P)
        uint160 sqrtPriceX96;
        // Current tick
        int24 tick;
        // Most recent observation index
        uint16 observationIndex;
        // Maximum number of observations
        uint16 observationCardinality;
        // Next maximum number of observations
        uint16 observationCardinalityNext;
    }
    ...

observationIndex 记录最新的观测的编号；
observationCardinality 记录活跃的观测数量；
observationCardinalityNext 记录观测数组能够扩展到的下一个基数的大小。

观测存储在一个定长的数组里，当一个新的观测被存储并且 observationCardinalityNext 超过 observationCardinality 的时候就会扩展。如果一个数组不能被扩展（下一个基数与现在的基数相同），旧的观测就会被覆盖，例如一个观测存储在下标 0，下一个就存储在下标 1，以此类推。

当池子创建的时候，observationCardinality 和 observationCardinalityNext 都设置为 1：

// src/UniswapV3Pool.sol
contract UniswapV3Pool is IUniswapV3Pool {
    function initialize(uint160 sqrtPriceX96) public {
        ...

        (uint16 cardinality, uint16 cardinalityNext) = observations.initialize(
            _blockTimestamp()
        );

        slot0 = Slot0({
            sqrtPriceX96: sqrtPriceX96,
            tick: tick,
            observationIndex: 0,
            observationCardinality: cardinality,
            observationCardinalityNext: cardinalityNext
        });
    }
}

// src/lib/Oracle.sol
library Oracle {
    ...
    function initialize(Observation[65535] storage self, uint32 time)
        internal
        returns (uint16 cardinality, uint16 cardinalityNext)
    {
        self[0] = Observation({
            timestamp: time,
            tickCumulative: 0,
            initialized: true
        });

        cardinality = 1;
        cardinalityNext = 1;
    }
    ...
}

写入观测

在 swap 函数中，当现价改变时，一个观测会被写入观测数组：

// src/UniswapV3Pool.sol
contract UniswapV3Pool is IUniswapV3Pool {
    function swap(...) public returns (...) {
        ...
        if (state.tick != slot0_.tick) {
            (
                uint16 observationIndex,
                uint16 observationCardinality
            ) = observations.write(
                    slot0_.observationIndex,
                    _blockTimestamp(),
                    slot0_.tick,
                    slot0_.observationCardinality,
                    slot0_.observationCardinalityNext
                );
            
            (
                slot0.sqrtPriceX96,
                slot0.tick,
                slot0.observationIndex,
                slot0.observationCardinality
            ) = (
                state.sqrtPriceX96,
                state.tick,
                observationIndex,
                observationCardinality
            );
        }
        ...
    }
}

注意到，这里观测的 tick 是 slot0_.tick（而不是 state.tick），也即这笔交易之前的价格！它在下一条语句中更新为新的价格。这正是我们之前讨论到的防价格操控机制：Uniswap 记录这个区块第一笔交易之前的价格，以及上一个区块最后一笔交易之后的价格。

另外要注意到，每个观测都通过 _blockTimestamp() 来标识，也即现在区块的时间戳。这意味着如果现在区块已经存在一个观测了，那么价格将不会被记录。如果当前区块没有观测（也即这是本区快中的第一笔 Uniswap 交易），价格才会被记录。这也是防价格操控机制的一部分。

// src/lib/Oracle.sol
function write(
    Observation[65535] storage self,
    uint16 index,
    uint32 timestamp,
    int24 tick,
    uint16 cardinality,
    uint16 cardinalityNext
) internal returns (uint16 indexUpdated, uint16 cardinalityUpdated) {
    Observation memory last = self[index];

    if (last.timestamp == timestamp) return (index, cardinality);

    if (cardinalityNext > cardinality && index == (cardinality - 1)) {
        cardinalityUpdated = cardinalityNext;
    } else {
        cardinalityUpdated = cardinality;
    }

    indexUpdated = (index + 1) % cardinalityUpdated;
    self[indexUpdated] = transform(last, timestamp, tick);
}

这里我们看到，如当前区块已经存在一个观测，那么将会跳过写。如果现在没有存在这样的观测，我们将会存储一个新的，并且在可能的时候尝试扩展基数。取模运算符(%)确保了观测的下标保持在 $[0, cardinality)$ 区间中，并且当达到上界时重置为 0。

接下来，我们来看一下 transform 函数：

function transform(
    Observation memory last,
    uint32 timestamp,
    int24 tick
) internal pure returns (Observation memory) {
    uint56 delta = timestamp - last.timestamp;

    return
        Observation({
            timestamp: timestamp,
            tickCumulative: last.tickCumulative +
                int56(tick) *
                int56(delta),
            initialized: true
        });
}

在这里，我们计算的是累积价格：现在的 tick 乘以上次观测到现在的秒数，并加到上一个累积价格之上。

增加基数

现在，让我们来看一下基数是如何扩展的。

任何人在任何时间都可以扩展一个池子中观测的基数，并为此支付 gas。因此，我们需要在池子合约中增添一个新的 public 的函数：

// src/UniswapV3Pool.sol
function increaseObservationCardinalityNext(
    uint16 observationCardinalityNext
) public {
    uint16 observationCardinalityNextOld = slot0.observationCardinalityNext;
    uint16 observationCardinalityNextNew = observations.grow(
        observationCardinalityNextOld,
        observationCardinalityNext
    );

    if (observationCardinalityNextNew != observationCardinalityNextOld) {
        slot0.observationCardinalityNext = observationCardinalityNextNew;
        emit IncreaseObservationCardinalityNext(
            observationCardinalityNextOld,
            observationCardinalityNextNew
        );
    }
}

以及 Oracle 合约中的一个新函数：

// src/lib/Oracle.sol
function grow(
    Observation[65535] storage self,
    uint16 current,
    uint16 next
) internal returns (uint16) {
    if (next <= current) return current;

    for (uint16 i = current; i < next; i++) {
        self[i].timestamp = 1;
    }

    return next;
}

在 grow 函数中，我们通过把 timestamp 值设置为一些非零值来分配这些新的观测。注意到，self 是一个 storage 的变量，为它的元素分配值会更新数组计数器，并且把这些值写道合约的存储中。

读取观测

最后我们来到了这章中最棘手的一个部分：读取观测。在开始之前，我们来复习一下观测是如何存储的，以便于我们更好地理解。

观测是存储在一个长度可扩展的定长数组中：

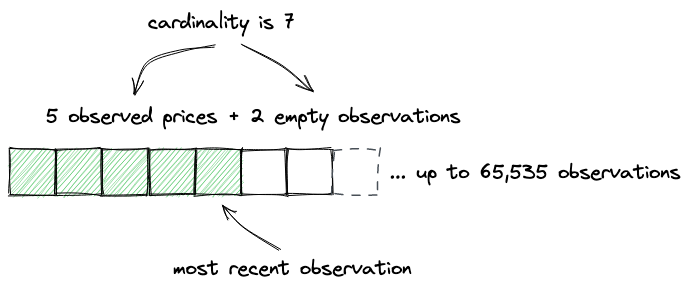
Observations array

正如我们上面所说，观测是可以溢出的：如果一个新的观测不能直接塞进数组，写操作会重新从下标0开始，也即最老的观测将会被覆盖：

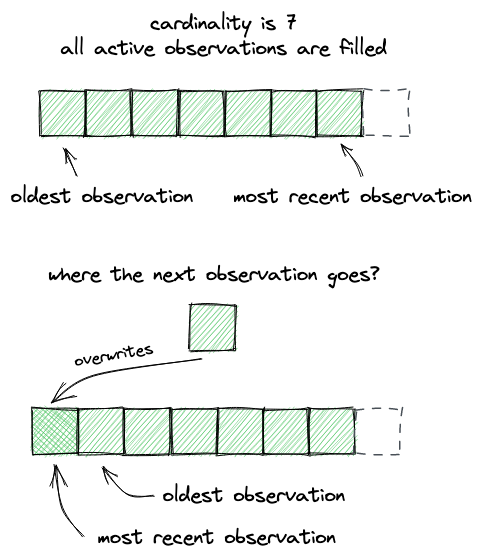
Observations wrapping

并不是每个区块都保证存在观测，因为交易并不一定在每个区块中都有。因此，会存在一些区块我们不知道价格，并且这样缺失的观测可能会很多。当然，我们并不希望在我们预言机提供的价格之间有很大空缺，这也是我们为什么使用时间加权平均价格（TWAP）——这样我们可以在没有观测的地方使用平均价格。TWAP 让我们能够做价格插值，即在两个观测之间画一条线，每个在这条线上的点都是两个观测之间某个时间戳对应的价格。

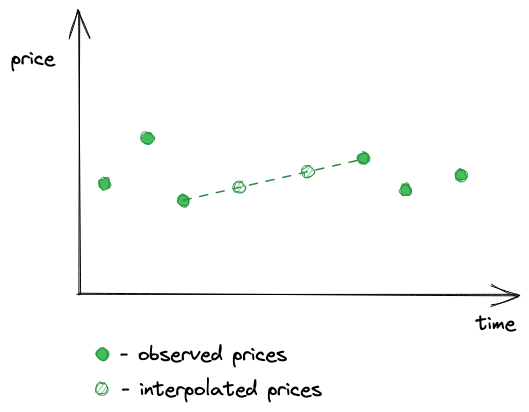
Interpolated prices

因此，读取观测意味着通过时间戳寻找到观测，并且在确实的观测处插值，同时要考虑到观测数组是可以溢出的（即数组中最老的观测可以在最新的观测之后）。由于我们并不是用时间戳作为下标来索引观测（为了节省 gas），我们需要使用二分查找算法来更有效地查找。但并不总是如此。

让我们来把它拆解成更小的步骤，首先来实现 Oracle 库中的 observe 函数：

function observe(
    Observation[65535] storage self,
    uint32 time,
    uint32[] memory secondsAgos,
    int24 tick,
    uint16 index,
    uint16 cardinality
) internal view returns (int56[] memory tickCumulatives) {
    tickCumulatives = new int56[](secondsAgos.length);

    for (uint256 i = 0; i < secondsAgos.length; i++) {
        tickCumulatives[i] = observeSingle(
            self,
            time,
            secondsAgos[i],
            tick,
            index,
            cardinality
        );
    }
}

这个函数接受当前区块时间戳，我们希望获取价格的时间点列表(secondsAgo)，现在的 tick、观测下标以及基数，作为参数。

接下来看一下 observeSingle 函数：

function observeSingle(
    Observation[65535] storage self,
    uint32 time,
    uint32 secondsAgo,
    int24 tick,
    uint16 index,
    uint16 cardinality
) internal view returns (int56 tickCumulative) {
    if (secondsAgo == 0) {
        Observation memory last = self[index];
        if (last.timestamp != time) last = transform(last, time, tick);
        return last.tickCumulative;
    }
    ...
}

在请求观测时，我们需要在二分查找之前进行一些检查：

如果请求的时间点是最新的观测，我们可以返回最新观测中的数据；
如果请求的时间点是在最新的观测之后，我们可以调用 transform 来找到当前时间点上的累积价格（根据最新的观测）；
如果请求的时间点在最新观测之前，我们需要使用二分查找。

上面的代码片段执行了前两点，secondsAgo == 0 即代表请求当前区块的观测。接下来我们来看第三点：

function binarySearch(
    Observation[65535] storage self,
    uint32 time,
    uint32 target,
    uint16 index,
    uint16 cardinality
)
    private
    view
    returns (Observation memory beforeOrAt, Observation memory atOrAfter)
{
    ...

这个函数参数为现在的区块时间戳（time），请求价格的时间点（target），以及现在观测的索引和基数。它返回两个观测的区间，请求的时间点就在这个区间之中。

在初始化二分查找过程中，我们设置边界：

uint256 l = (index + 1) % cardinality; // oldest observation
uint256 r = l + cardinality - 1; // newest observation
uint256 i;

记得观测数组是可以溢出的，因此我们上面使用了模运算。

然后我们进入一个循环，每次检查区间的中点：如果它没有初始化（那里没有观测），我们将会进入下一个循环：

while (true) {
    i = (l + r) / 2;

    beforeOrAt = self[i % cardinality];

    if (!beforeOrAt.initialized) {
        l = i + 1;
        continue;
    }

    ...

如果这个点已初始化，我们把它当做我们请求时间点所在区间的左边界。接下来我们尝试去验证右边界（atOrAfter）:

    ...
    atOrAfter = self[(i + 1) % cardinality];

    bool targetAtOrAfter = lte(time, beforeOrAt.timestamp, target);

    if (targetAtOrAfter && lte(time, target, atOrAfter.timestamp))
        break;
    ...

如果我们已经找到了边界，我们就直接返回。否则我们继续搜索：

    ...
    if (!targetAtOrAfter) r = i - 1;
    else l = i + 1;
}

在找到请求时间点所在的观测区间后，我们需要计算请求时间点的价格：

// function observeSingle() {
    ...
    uint56 observationTimeDelta = atOrAfter.timestamp -
        beforeOrAt.timestamp;
    uint56 targetDelta = target - beforeOrAt.timestamp;
    return
        beforeOrAt.tickCumulative +
        ((atOrAfter.tickCumulative - beforeOrAt.tickCumulative) /
            int56(observationTimeDelta)) *
        int56(targetDelta);
    ...

这部分很简单，就是求出在这个区间中价格变化的平均速率，乘以从下界到我们需要时间点之间的秒数。这就是我们之前讨论过的插值。

我们最后需要实现的就是池子合约中的一个 public 函数，读取并返回观测：

// src/UniswapV3Pool.sol
function observe(uint32[] calldata secondsAgos)
    public
    view
    returns (int56[] memory tickCumulatives)
{
    return
        observations.observe(
            _blockTimestamp(),
            secondsAgos,
            slot0.tick,
            slot0.observationIndex,
            slot0.observationCardinality
        );
}

解析观测

现在我们来看一下如何解析观测。

我们刚才实现的 observe 函数返回一个累积价格的数组，现在我们希望把它们转换成真正的价格。我会在 observe 函数的测试中解释如何实现这一点。

在测试中，我在不同区块、不同方向上执行了多笔不同的交易：

function testObserve() public {
    ...
    pool.increaseObservationCardinalityNext(3);

    vm.warp(2);
    pool.swap(address(this), false, swapAmount, sqrtP(6000), extra);

    vm.warp(7);
    pool.swap(address(this), true, swapAmount2, sqrtP(4000), extra);

    vm.warp(20);
    pool.swap(address(this), false, swapAmount, sqrtP(6000), extra);
    ...

vm.warp 是 Foundry 的一个 cheat code：它使用指定的时间戳产生一个新的区块——2,7,20 这些是区块时间戳。

第一笔交易发生在时间戳为2的区块，第二个在时间戳7，第三个在时间戳20。然后我们可以读取这些观测：

    ...
    secondsAgos = new uint32[](4);
    secondsAgos[0] = 0;
    secondsAgos[1] = 13;
    secondsAgos[2] = 17;
    secondsAgos[3] = 18;
    // 注意这里是secondsAgo，所以用20减去，能对应上面的每个时间戳
    int56[] memory tickCumulatives = pool.observe(secondsAgos);
    assertEq(tickCumulatives[0], 1607059);
    assertEq(tickCumulatives[1], 511146);
    assertEq(tickCumulatives[2], 170370);
    assertEq(tickCumulatives[3], 85176);
    ...

最早观测的价格是 0，即在池子部署时初始的观测。然而，由于我们设置的基数是 3，我们进行了3笔交易，它被最后一个观测覆盖了。
在第一笔交易中，观测到的 tick 是 85176，也即池子的初始价格——回忆一下，我们观测到的是区块中第一笔交易之前的价格。由于最早的一笔观测被覆盖掉了，这实际上是数组中最早的一个观测。
下一个返回的累计价格是 170370，也即 85176 + 85194。前者是之前的累积价格，后者是第一笔交易之后的价格，在下一个区块中被观测到。
下一个累积价格是 511146，即 (511146 - 170370) / (17 - 13) = 85194，在第二笔交易和第三笔交易之间的累积价格。
最后，最新的观测是 1607059，也即 (1607059 - 511146) / (20 - 7) = 84301，约为 4581 USDC/ETH，这事第二笔交易的价格，在第三笔交易中被观测到。

下面是一个包含了插值的测试样例：观测的时间点不是交易发生的时间点：

secondsAgos = new uint32[](5);
secondsAgos[0] = 0;
secondsAgos[1] = 5;
secondsAgos[2] = 10;
secondsAgos[3] = 15;
secondsAgos[4] = 18;

tickCumulatives = pool.observe(secondsAgos);
assertEq(tickCumulatives[0], 1607059);
assertEq(tickCumulatives[1], 1185554);
assertEq(tickCumulatives[2], 764049);
assertEq(tickCumulatives[3], 340758);
assertEq(tickCumulatives[4], 85176);

结果对应的价格分别是：4581.03, 4581.03, 4747.6, 5008.91，即对应间隔的平均价格。

如何在 Python 中计算这些价格：

vals = [1607059, 1185554, 764049, 340758, 85176]
secs = [0, 5, 10, 15, 18]
[1.0001**((vals[i] - vals[i+1]) / (secs[i+1] - secs[i])) for i in range(len(vals)-1)]

Web3 Uniswap Development Book