计算流动性
没有流动性就无法进行交易。为了能够完成我们的第一笔交易,我们首先需要向池子中添加一些流动性。 而为了向池子合约添加流动性,我们需要知道:
- 一个价格区间,即
LP希望他的流动性仅在这个区间上提供和被利用; - 提供流动性的数量,也即提供的两种代币的数量,我们需要将它们转入池子合约。
在本节中,我们会手动计算上述变量的值;在后续章节中,我们会在合约中对此进行实现。
首先我们来考虑价格区间。
价格区间计算
回忆一下上一章所讲,在 UniswapV3 中,整个价格区间被划分成了 ticks:
每个 tick 对应一个价格,以及有一个下标。
在我们的第一个实现中,我们的现货价格设置为 1 ETH , 5000 USDC。
- 购买
ETH会移除池子中的一部分ETH,从而使得ETH价格变得高于5000 USDC - 提供流动性的用户希望在一个包含此价格的区间中提供流动性,并且要确保最终的价格落在这个区间内。(跨区间的交易将会在后续章节提到)。
我们需要找到 价格区间上下限分别对应的 tick:
- 对应现货价格的
tick(1 ETH , 5000 USDC) - 提供流动性的价格区间上下界对应的
tick
- 在这里,下限为
4545 USDC - 上限为
5500 USDC
从之前的章节中我们知道下述公式:
$$ P = \frac{y}{x} = (1.0001)^{i}$$
$$i = log_{1.0001} P(i)$$
由于我们把 ETH 作为资产 $x$,USDC 作为资产 $y$,每个 tick 对应的值为:
$$ P_c = \frac{5000}{1} = 5000$$
$$P_l = \frac{4545}{1} = 4545$$
$$P_u = \frac{5500}{1} = 5500$$
在这里,$P_c$ 代表现货价格,$P_l$ 代表区间下界,$P_u$ 代表区间上界。
接下来,我们可以计算价格对应的 ticks。使用下面公式:
- 现价 tick: $i_c = log_{1.0001} 5000 \approx 85176$
- 下界 tick: $i_l = log_{1.0001} 4545 \approx 84222$
- 上界 tick: $i_u = log_{1.0001} 5500 \approx 86129$
上述计算使用的是 Python:
import math def price_to_tick(p): return math.floor(math.log(p, 1.0001)) price_to_tick(5000) > 85176
价格区间的计算就是这样。
V3 把$\sqrt{P}$ 存储为一个 Q64.96 类型的定点数,使用 64 位作为整数部分,使用 96 位作为小数部分。因此,价格的取值范围是 $[2^{-128}, 2^{128}]$
在我们上面的计算中,价格按照浮点数形式计算。我们需要将价格的平方根转换成 Q64.96 格式,也非常简单:只需要将这个数乘以 $2^{96}$,即可得到:
$$\sqrt{P_c} = \sqrt{5000} * 2 ^{96} = 5602277097478614198912276234240$$
$$\sqrt{P_l} = \sqrt{4545} * 2 ^{96} = 5314786713428871004159001755648$$
$$\sqrt{P_u} = \sqrt{5500} * 2 ^{96} = 5875717789736564987741329162240$$
在 Python 中:
q96 = 2**96 def price_to_sqrtp(p): return int(math.sqrt(p) * q96) price_to_sqrtp(5000) > 5602277097478614198912276234240注意先进行乘法再取整,否则会损失精度
Token 数量计算
接下来,我们需要决定向池子中投入多少 token。
答案是:越多越好。数量并没有严格定义,我们质押的数目越多,购买同样数量的 ETH 就会使得价格的变动越小,防止离开我们的价格区间。
在开发和测试智能合约的过程中,我们可以获得任意数量的 token,所以钱不是问题。
为了实现我们的第一笔交易,我们将会在池子中质押 1 ETH , 5000 USDC
要记得池子中资产数量的比例决定了现货价格。所以假设我们希望像池子中投入更多的资产而保持现货价格不变,我们投入的资产也必须满足同样的比例,例如:2 ETH 和 10,000 USDC;10 ETH 和 50,000 USDC。
流动性数量计算
接下来,我们将基于我们质押 token 的数量计算流动性 $L$ 的值。
根据之前我们提到过的公式,流动性数量如下计算:
$$L = \sqrt{xy}$$
然而,上述公式是用于无穷价格区间曲线,但我们希望的是把流动性放在某个有界的价格区间,也即无穷曲线的一部分。 我们需要针对我们希望流动性存在的价格区间来计算对应的 $L$,因此可能需要一些更复杂的计算。
为了计算这个价格区间的 $L$,我们来回顾我们之前讨论过的一个有趣的点:
价格区间可以被耗尽。
我们可以将一个价格区间的某种 token 全部买走,使得该区间中只有另一种 token:
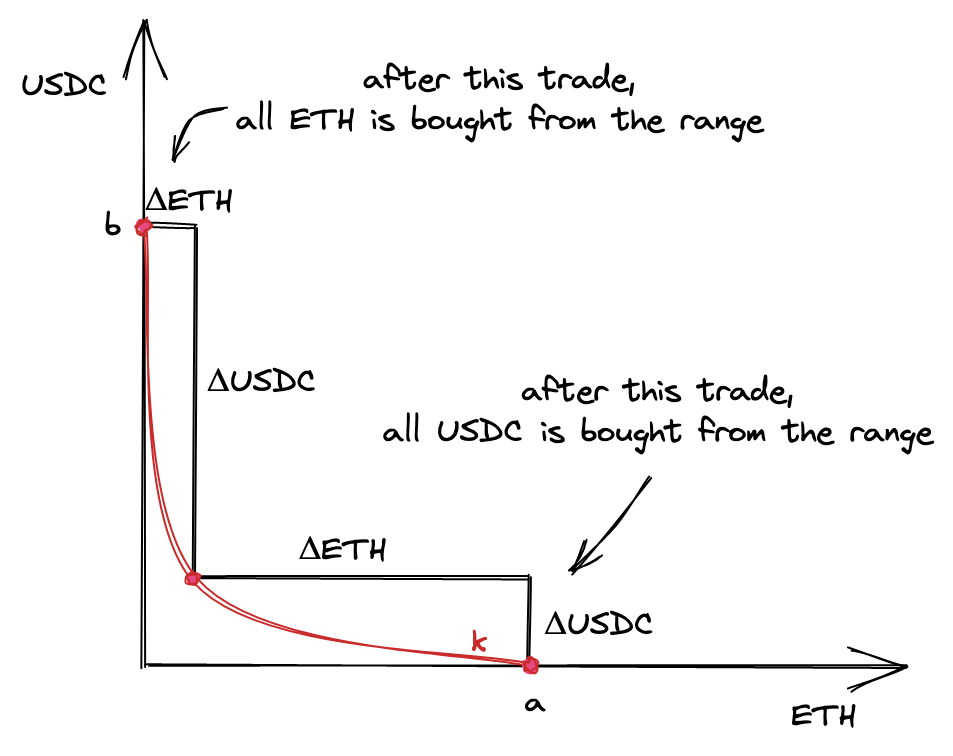
在上图中的两个边界点,区间流动性池中都只有一种 token:
在 $a$ 点池子里只有 ETH,在 $b$ 点只有 USDC。
也就是说,我们希望能够找到一个 $L$,使得价格能够移动到两个端点处。 我们需要足够的流动性来使得价格能够达到上下界,因此,我们会希望通过 $\Delta x$ 和 $\Delta y$ 的最大值来计算流动性。
现在我们来看一下边界点的价格。当从池子中购买 ETH 时,池子中的 ETH 减少,ETH 的价格会升高;
当从池子中使用 ETH 购买 USDC时,池子中的 ETH 数量会增加,同时 ETH 的价格会下跌。
由于价格为 $\frac{y}{x}$,所以 $a$ 点为价格最低点,$b$ 点为价格最高点。
事实上,按照公式,在这两个点的价格是没有定义的,因为池子中只有一种 token,但是我们在这里只需要理解,$b$ 点的价格高于起始价格,$a$ 点价格低于起始价格即可。
现在,我们将图中的曲线分为两部分:起始点左边和起始点右边。
我们将在两边分别计算出 $L$。
为什么会有两个?
这是因为,在交易过程中,价格会朝着某个方向移动:升高或降低。对于价格的移动,仅有一种 token 会起作用:
左半边由 token $x$ 随着价格升高不断减少,右半边由 token $y$ 随着价格升高也是不断减少
- 当
token x价格升高时,表示池子中的token x的数量减少,因此推高token x价格的交易大多应该是从池子中购买token x - 当
token x价格下降时,表示池子中的token x的数量增加,因此降低token x价格的交易大多应该是从池子中购买token y,往池子中注入更多的token x
因此,导致价格升到左半边顶点 b 的交易应该是通过用户不断购入 token x 提供,因此只通过 token x 数量计算出来
类似地,导致价格降到右半边低点 a 的交易应该是通过用户不断购入 token y 提供,因此只通过 token y 数量计算出来
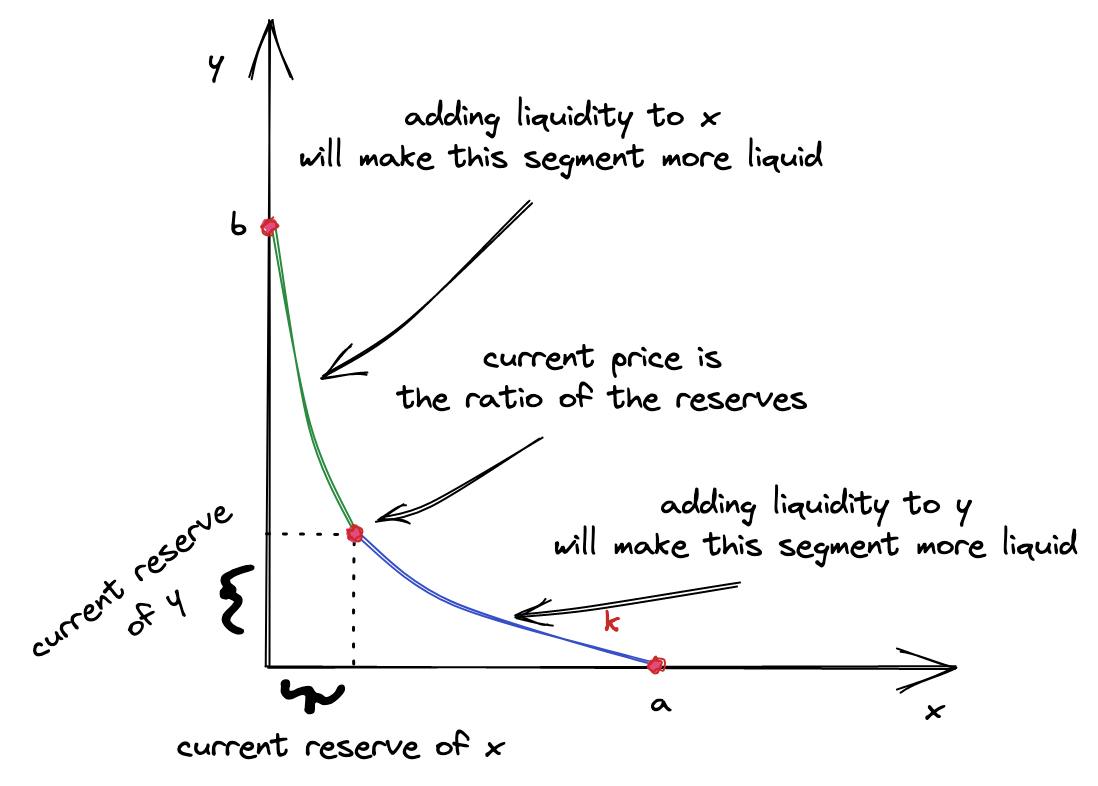
这也是为什么,我们会计算出两个不同的 $L$ 并选择其中一个。
选择哪个呢?
选择较小的值。因为较大的那个流动性包含了较小的流动性。我们希望流动性均匀分布在我们所提供的价格区间中,因此左右提供的流动性需要保持一致。如果我们选择较大的那个,用户所提供的某种 token 的数量可能会大于其指定的数量,来平衡两边的流动性。这的确理论上是可行的,但是会让整个智能合约变得更加复杂。
那么,较大的 $L$ 怎么办呢?实际上是没有用的。我们挑选小的那个 $L$,并且计算出这个 $L$ 对应的较大的 $L$ 那边 token 的数量——会比之前的要小。这样,两边的流动性就相同了,都等于较小值。
最后还需要说明的一个关键点是:新的流动性需要保证不改变现货价格。也即,它必须与现在两种资产的数量成比例。这也是为什么我们上面会计算出两个 $L$ ——因为仅考虑了一种资产,而没有保证比例。我们选择较小的那个 $L$ 来重新计算比例。
上面的说明有些绕,或许在后面实现代码的过程中我们会对此理解更清晰吧。现在我们来看公式。
回忆一下, $\Delta x$ 和 $\Delta y$ 的计算公式为:
$$\Delta x = \Delta \frac{1}{\sqrt{P}} L$$ $$\Delta y = \Delta \sqrt{P} L$$
我们把上述公式中的 $\Delta \sqrt{P}$ 相关部分展开:
$$\Delta x = (\frac{1}{\sqrt{P_c}} - \frac{1}{\sqrt{P_b}}) L$$ $$\Delta y = (\sqrt{P_c} - \sqrt{P_a}) L$$
$P_a$ 是 $a$ 点的价格,$P_b$ 是 $b$ 点的价格, $P_c$ 是现货价格。
我们接下来根据第一个公式推导出计算 $L$ 的公式:
$$\Delta x = (\frac{1}{\sqrt{P_c}} - \frac{1}{\sqrt{P_b}}) L$$ $$\Delta x = \frac{L}{\sqrt{P_c}} - \frac{L}{\sqrt{P_b}}$$ $$\Delta x = \frac{L(\sqrt{P_b} - \sqrt{P_c})}{\sqrt{P_b} \sqrt{P_c}}$$ $$L = \Delta x \frac{\sqrt{P_b} \sqrt{P_c}}{\sqrt{P_b} - \sqrt{P_c}}$$
从第二个公式推导: $$\Delta y = (\sqrt{P_c} - \sqrt{P_a}) L$$ $$L = \frac{\Delta y}{\sqrt{P_c} - \sqrt{P_a}}$$
这就是我们的两个 $L$ 的计算公式,跟别对应起始点两边的两段曲线:
$$L = \Delta x \frac{\sqrt{P_b} \sqrt{P_c}}{\sqrt{P_b} - \sqrt{P_c}}$$ $$L = \frac{\Delta y}{\sqrt{P_c} - \sqrt{P_a}}$$
接下来,我们把之前计算出的价格代入公式:
$$L = \Delta x \frac{\sqrt{P_b}\sqrt{P_c}}{\sqrt{P_b}-\sqrt{P_c}} = 1 ETH * \frac{\sqrt{5500} * \sqrt{5000}}{\sqrt{5500} - \sqrt{5000}}$$ 转换成 Q64.96 后得到:
$$L = 1519437308014769733632$$
对于另一个 $L$: $$L = \frac{\Delta y}{\sqrt{P_c}-\sqrt{P_a}} = \frac{5000USDC}{\sqrt{5000} - \sqrt{4500}}$$ $$L = 1517882343751509868544$$
两者中,我们选择小的那一个
Python 计算:
sqrtp_low = price_to_sqrtp(4545) sqrtp_cur = price_to_sqrtp(5000) sqrtp_upp = price_to_sqrtp(5500) def liquidity0(amount, pa, pb): if pa > pb: pa, pb = pb, pa return (amount * (pa * pb) / q96) / (pb - pa) def liquidity1(amount, pa, pb): if pa > pb: pa, pb = pb, pa return amount * q96 / (pb - pa) liq0 = liquidity0(amount_eth, sqrtp_cur, sqrtp_upp) liq1 = liquidity1(amount_usdc, sqrtp_cur, sqrtp_low) liq = int(min(liq0, liq1)) > 1517882343751509868544
重新计算 token 数量
尽管我们初始选择了我们想要质押的 token 数目,这个数目可能并不准确。
我们并不能在任何价格区间质押任何比例的 token 来获取流动性,因为流动性需要满足在价格区间的曲线上均匀分布。
因此,尽管用户选择了起始数量,合约会对它们重新计算,所以实际的数量会略有不同(至少会有取整的精度问题)
幸运的是,我们已经获得了对应的公式:
$$\Delta x = \frac{L(\sqrt{P_b} - \sqrt{P_c})}{\sqrt{P_b} \sqrt{P_c}}$$ $$\Delta y = L(\sqrt{P_c} - \sqrt{P_a})$$
在 Python 中:
def calc_amount0(liq, pa, pb): if pa > pb: pa, pb = pb, pa return int(liq * q96 * (pb - pa) / pa / pb) def calc_amount1(liq, pa, pb): if pa > pb: pa, pb = pb, pa return int(liq * (pb - pa) / q96) amount0 = calc_amount0(liq, sqrtp_upp, sqrtp_cur) amount1 = calc_amount1(liq, sqrtp_low, sqrtp_cur) (amount0, amount1) > (998976618347425408, 5000000000000000000000)正如上述计算结果,得到的数据基本等于我们想要提供的数量,不过 ETH 略少一点
Hint: 使用
cast --from-wei AMOUNT来把wei转换成ether, 示例:
cast --from-wei 998976618347425280输出0.998976618347425280.